数学二高数公式总结

本篇因为是考试后写的，虽然保不准也算下一次考试前，创作初衷也就今天突然想总结一下之前一直在用的公式，周期可能也就这两天，但参考了一些别人的博文或者帖子，觉得还是与自己想的侧重点有点不太一样，所以就有了上面这张思维导图的大纲，如果不太完整的地方，后期我会去尽量完善，本篇公式有些图是我自己做的，有些是参考文献中引用的几篇知乎帖子，考虑到公式美观性，与参考文献也没有对公式加上水印，所以本篇大部分图片都去除了，希望能作为以后的备用资料。

极限

极限的概念与性质

两个重要极限：
$$\begin{array}{rl}& \underset{x\to 0}{\lim }\frac{\sin x}{x}=1\\ & \\ & \underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=\mathrm{e}\end{array}$$

无穷小阶的概念与比较

$$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\{\begin{array}{ll}l\ne 0\text{ 且 }\ne 1,& f(x)\text{ 与 }g(x)\text{ 同阶而不等价, }\\ 1,& f(x)\text{ 与 }g(x)\text{ 等价 }\\ 0,& f(x)\text{ 比 }g(x)\text{ 高阶 }\\ \infty ,& f(x)\text{ 比 }g(x)\text{ 低阶 }\end{array}$$

无穷小阶过程与方式

常用等价无穷小：

导数

基本求导公式

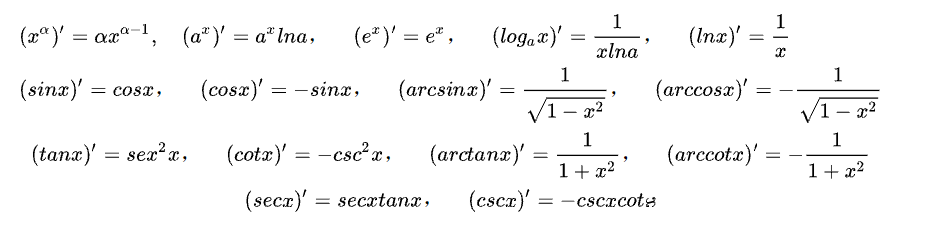
n阶导数

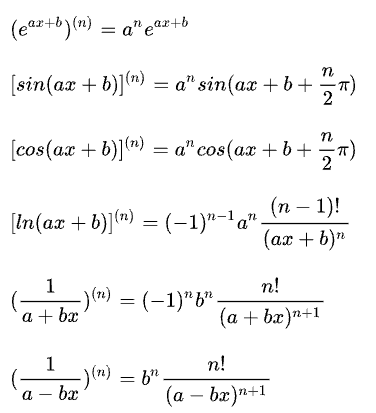
泰勒公式及其应用

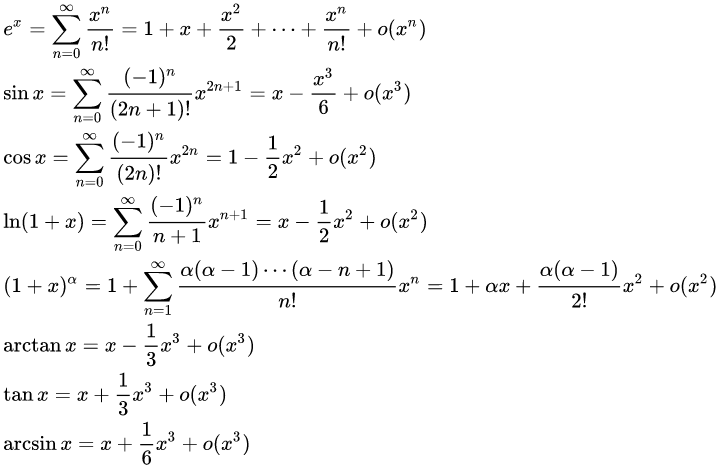
一元微分几何与物理应用

反函数求导公式：
$$\begin{array}{rl}& {\phi }^{\prime }(x)=\frac{dx}{dy}=\frac{1}{f^{\prime }(x)}\\ & \\ & {\phi }^{\prime \prime }(x)=\frac{d^{2}x}{d{y}^2}=-\frac{f^{\prime \prime }(x)}{f^{\prime 3}(x)}\end{array}$$

参数方程求导公式：

设$y=y(x)$是由$\{\begin{array}{l}x=\phi (t)\\ y=\psi (t)\end{array}$所组成的参数方程，则一阶求导为：

$$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{{\psi }^{\prime }(t)}{{\phi }^{\prime }(t)}$$

二阶求导为：
$$\frac{d^{2}y}{d{x}^2}=\frac{d\left(\frac{dy}{dx}\right)}{dx}=\frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{dx/dt}=\frac{\left[\frac{\psi (t)}{\phi (t)}\right]}{{\phi }^{\prime }(t)}=\frac{{\psi }^{\prime \prime }(t){\phi }^{\prime }(t)-{\psi }^{\prime }(t){\phi }^{\prime \prime }(t)}{{\phi }^{\prime 3}(t)}$$

常用曲率计算公式：

微分中值定理

渐近线

罗尔定理

定义：

设$f(x)$在$[a,b]$上连续，在(a,b)内可导，又$f(a)=f(b)$，则$\exists \xi \in \left(a,b\right)$使得$f^{\prime }\left(\xi \right)=0$

图形：

拉格朗日定理

定义：

设$f(x)$在$[a,b]$上连续，在(a,b)内可导，则$\exists \xi \in \left(a,b\right)$使得$f\left(b\right)-f\left(a\right)=f^{\prime }\left(\xi \right)\left(b-a\right)$

图形：

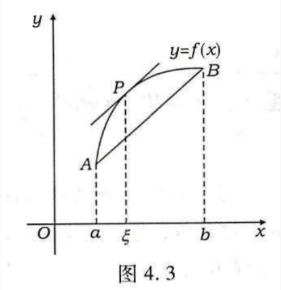
等价形式：
$$f(b)-f(a)=f^{\prime }(a+\theta (b-a))(b-a),0<\theta <1$$

柯西定理

定义：

设$f(x)$在$[a,b]$上连续，在(a,b)内可导且$g^{\prime }\left(x\right)\ne 0$，则$\exists \xi \in \left(a,b\right)$使得$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}$，即为：

$$F(x)=f(x)-f(a)-\frac{f(b)-f(a)}{g(b)-g(a)}[g(x)-g(a)]$$

定积分与应用

定积分公式

常用分部积分

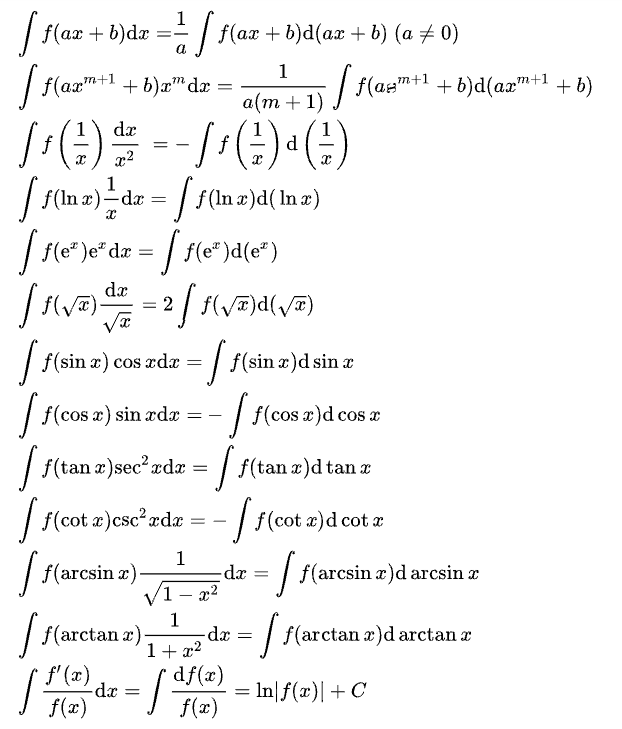
伽玛函数积分

（有这一章是因为去年李林卷有很多这方面的题，虽然最后没考但复习了）

伽玛函数基本公式为：

$$\Gamma (\alpha )={\int }_0^{+\infty }{x}^{\alpha -1}{e}^{-x}dx\stackrel{x=t^2}{=}2{\int }_0^{+\infty }{t}^{2\alpha -1}{e}^{-t^2}dt$$

下面是一些最常用能直接得出结果的公式：

华莱士公式与相关

反常积分

这一节还有很多内容可以重点讲的，因为22真题考得反常积分很有技巧性，不过这里只提基础公式，而且目前我还理解不到位，到时候可以专门写一节这的博客，虽然我当初走了很多弯路，但所幸最后会了，主要是很多机构讲本节内容都一成不变，22命题组应该抓住了这个问题，技巧性碾压了，23一些考研机构希望有所改善。

一元函数积分学的几何应用

1. 面积：

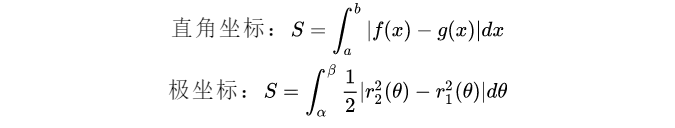
2.平面曲线弧长：

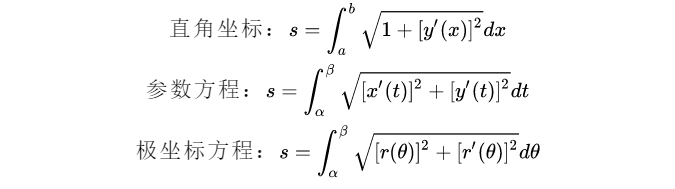
3.旋转体体积：

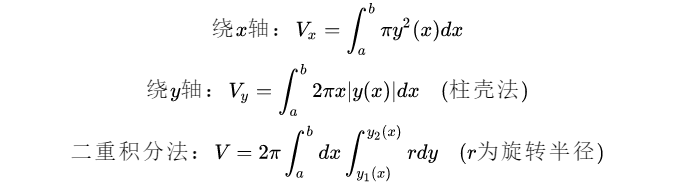
4.旋转曲面侧面积(x轴)：

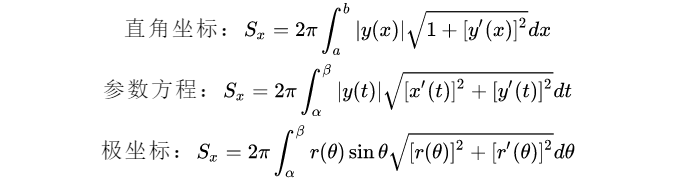
5.质心：

一元函数积分学的物理应用

物理应用主要包括主要包括:变力沿直线做功、液体压力、万有引力、质心、形心以及函数的平均值与均方根。

均匀密度平面图形的质心（形心）：

$$\bar{x}=\frac{M_y}{M}=\bar{x}=\frac{{\iint }_{D}x\rho (x,y)dxdy}{{\iint }_D\rho (x,y)dxdy}=\frac{{\int }_a^{b}x[f(x)-g(x)]\mathrm{d}x}{{\int }_a^b[f(x)-g(x)]\mathrm{d}x}$$

$$\bar{y}=\frac{M_x}{M}=\bar{y}=\frac{{\iint }_{D}y\rho (x,y)dxdy}{{\iint }_D\rho (x,y)dxdy}=\frac{\frac{1}{2}{\int }_a^b\left[f^2(x)-g^2(x)\right]\mathrm{d}x}{{\int }_a^b[f(x)-g(x)]\mathrm{d}x}$$

均匀线密度为$p$的平面曲线的质心（形心）：

自变量为t的参数方程：
$$\bar{x}=\frac{{\int }_{\alpha }^{\beta }\phi (t)\sqrt{{\phi }^{\prime 2}(t)+{\psi }^{\prime 2}(t)}\mathrm{d}t}{{\int }_{\alpha }^{\beta }\sqrt{{\phi }^{\prime 2}(t)+{\psi }^{\prime 2}(t)}\mathrm{d}t}$$

$$\bar{y}=\frac{{\int }_{\alpha }^{\beta }\psi (t)\sqrt{{\phi }^{\prime 2}(t)+{\psi }^{\prime 2}(t)}\mathrm{d}t}{{\int }_{\alpha }^{\beta }\sqrt{{\phi }^{\prime 2}(t)+{\psi }^{\prime 2}(t)}\mathrm{d}t}$$

至于做功、压力、引力还有均方根好像不太好总结，另外不论预测题还是真题的频率也不高，这里先略过。

积分线区域

6.各种线段对应的直角坐标与极坐标图形与表示：

关于玫瑰线可得到结论为当 n 是奇数时，玫瑰线有 n 个花瓣，称为 n 叶玫瑰。当 n 是偶数时，玫瑰线有 2n 个花瓣，为 2n 叶玫瑰。也可通过maple画出动态图为：

根据wiki对于Rose curve的解析，引用其里面的例子，具有以下形式的极坐标方程的玫瑰的总面积公式为：

$$\begin{array}{rl}& \frac{1}{2}{\int }_0^{2\pi }(a\cos (k\theta ){)}^{2}d\theta =\frac{a^2}{2}\left(\pi +\frac{\sin (4k\pi )}{4k}\right)=\frac{\pi a^2}{2}\\ & \\ & \frac{1}{2}{\int }_0^{\pi }(a\cos (k\theta ){)}^{2}d\theta =\frac{a^2}{2}\left(\frac{\pi }{2}+\frac{\sin (2k\pi )}{4k}\right)=\frac{\pi a^2}{4}\end{array}$$

其它的就不再这里举例了，李林这里的题目覆盖得很全面。

多元微分

多元微分的偏导定义

偏导数几何定义：

对$x$：
$$\frac{\partial f\left(x_0,y_0\right)}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(x_0+\Delta x,y_0\right)-f\left(x_0,y_0\right)}{\Delta x}$$

对$y$：
$$\frac{\partial f\left(x_0,y_0\right)}{\partial y}=\underset{\Delta y\to 0}{\lim }\frac{f\left(x_0,y_0+\Delta y\right)-f\left(x_0,y_0\right)}{\Delta y}$$

高阶偏导数公式：

$$\begin{array}{ll}\frac{{\partial }^{2}z}{\partial x^2}=\frac{\partial }{\partial x}\left(\frac{\partial z}{\partial x}\right)=f_{xx}^{\prime \prime }(x,y),& \frac{{\partial }^{2}z}{\partial x\partial y}=\frac{\partial }{\partial y}\left(\frac{\partial z}{\partial x}\right)=f_{xy}^{\prime \prime }(x,y)\\ & \\ \frac{{\partial }^{2}z}{\partial y\partial x}=\frac{\partial }{\partial x}\left(\frac{\partial z}{\partial y}\right)=f_{yx}^{\prime \prime }(x,y),& \frac{{\partial }^{2}z}{\partial y^2}=\frac{\partial }{\partial y}\left(\frac{\partial z}{\partial y}\right)=f_{yy}^{\prime \prime }(x,y)\end{array}$$

复合求导公式（链式法则）：

$$\begin{array}{rl}\frac{\partial z}{\partial x}& =\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}\\ & \\ \frac{\partial z}{\partial y}& =\frac{\partial f}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial y}\end{array}$$

雅克比：

多元函数极值的充要条件

充分条件：

$$\text{ 设 }z=f(x,y)\text{ 在点 }\left(x_0,y_0\right)\text{ 的某邻域内连续且有一阶及二阶连续偏导数, 又 }{f}_x^{\prime }\left(x_0,y_0\right)=0,f_y^{\prime }\left(x_0,y_0\right)=0\text{, 令 }{f}_{xx}^{\prime \prime }\left(x_0,y_0\right)=A,f_{xy}^{\prime \prime }\left(x_0,y_0\right)=B,f_{yy}^{\prime \prime }\left(x_0,y_0\right)=C\text{, 则 }$$

$$AC-B^2=\{\begin{array}{ll}<0,& \left(x_0,y_0\right)\text{ 不是 }f(x,y)\text{ 的极值点 }\\ >0,& \{\begin{array}{l}A>0,\text{ 极小值 }\\ A<0,\text{ 极大值 }\end{array}\\ =0,& \text{ 可能取极值, 也可能不取极值, 需另做讨论 (一般用极值定义) }\end{array}$$

必要条件：

某点处两个偏导数等于0

拉格朗日乘数法

二重积分

二重积分概念

直角坐标：

先对 $y$ 后对 $x$ ：

$${\iint }_{D}f(x,y)d\sigma ={\int }_a^{b}dx{\int }_{{\varphi }_1(x)}^{{\varphi }_2(x)}f(x,y)dy$$

先对$x$ 后对 $y$：

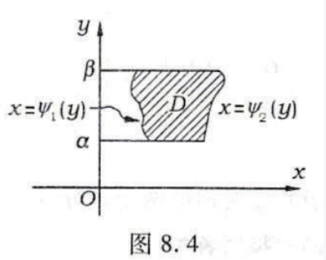
$${\iint }_{D}f(x,y)\mathrm{d}\sigma ={\int }_{\alpha }^{\beta }\mathrm{d}y{\int }_{{\psi }_1(y)}^{{\psi }_2(y)}f(x,y)\mathrm{d}x$$

极坐标系：

因为变化很多，所以这里略过。

对称区域二重积分

二重积分图形域

二重积分的图形域见定积分图形域。本章公式总结内容较少，除了很多我感觉没必要以外，其余的大多都需要结合图形一起表述，比如分块重积分，直接坐标与极坐标相互转换以及坐标轴平移变换，这种没有固定式子可写，题目也往往会出很多不规则的图形进行分割求解，画对图形域，答案就对了大半，22真题我在这里吃了大亏。

微分方程

一阶线性齐次方程

1. 可分离变量的微分方程：

$$\frac{\mathrm{d}y}{\mathrm{d}x}=f(x,y)\text{, 其中 }f(x,y)={\phi }_1(x){\phi }_2(y)$$

解法：
$$\begin{array}{rl}\frac{\mathrm{d}y}{\mathrm{d}x}=f(x,y)& \Rightarrow \frac{\mathrm{d}y}{\mathrm{d}x}={\phi }_1(x){\phi }_2(y)\\ & \Rightarrow \frac{\mathrm{d}y}{{\phi }_2(y)}={\phi }_1(x)\mathrm{d}x\\ & \Rightarrow \int \frac{\mathrm{d}y}{{\phi }_2(y)}=\int {\phi }_1(x)\mathrm{d}x+C\end{array}$$

2.齐次微分方程
$$\frac{\mathrm{d}y}{\mathrm{d}x}=f(x,y)\text{, 其中 }f(x,y)=\phi \left(\frac{y}{x}\right)$$

解法：

3.一阶齐次线性微分方程
$$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=0$$

解法：
$$y=C{\mathrm{e}}^{-\int P(x)dx}\text{ (其中 }C\text{ 为任意常数) }$$

非线性微分方程公式

$$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)$$

解法：

$$y=\left[\int Q(x){\mathrm{e}}^{\int P(x)dx}\mathrm{d}x+C\right]{\mathrm{e}}^{-\int P(x)dx}$$
(其中 $C$ 为任意常数)

微分方程的各种性质

这一小节主要与一些充要条件判断有关，常与方程组联系起来，这里略过，后续可能补充。

高阶线性微分方程

可直接写出表达式：

表达式推导与高阶方程解法：

Reference：

[1]. https://zhuanlan.zhihu.com/p/200968718

[2]. https://zhuanlan.zhihu.com/p/106252437

[3]. 考研辅导讲义