本文仅代表个人观点,才疏学浅,欢迎指正。
数学分析
复习以下高等数学中梯度的相关知识:
z = f ( x , y ) = 1 a x 2 + b y 2 (1) z=f(x,y)=\frac{1}{ax^2+by^2}\tag{1} z=f(x,y)=ax2+by21(1)
∂ f ∂ x = − 2 a x ( a x 2 + b y 2 ) 2 (2) \frac{\partial f}{\partial x}=-\frac{2ax}{(ax^2+by^2)^2}\tag{2} ∂x∂f=−(ax2+by2)22ax(2)
∂ f ∂ y = − 2 b y ( a x 2 + b y 2 ) 2 (3) \frac{\partial f}{\partial y}=-\frac{2by}{(ax^2+by^2)^2}\tag{3} ∂y∂f=−(ax2+by2)22by(3)
g r a d z = − 2 a x ( a x 2 + b y 2 ) 2 i + − 2 b y ( a x 2 + b y 2 ) 2 j (4) grad{\,}z=-\frac{2ax}{(ax^2+by^2)^2}i+-\frac{2by}{(ax^2+by^2)^2}j\tag{4} gradz=−(ax2+by2)22axi+−(ax2+by2)22byj(4)
在公式1中,a、b为常量,x、y为变量。公式2、公式3为公式1的偏导数,公式4为公式1的梯度。公式1在三维空间中为一个漏斗形曲面,越靠近(0, 0)值越小。grad z为曲面上各个位置函数值下降最快的方向,有两个分量均为(x, y)的函数。
- 当(a, b) = (1, 1)时
g r a d z = − 2 x ( x 2 + y 2 ) 2 i + − 2 y ( x 2 + y 2 ) 2 j (5) grad{\,}z=-\frac{2x}{(x^2+y^2)^2}i+-\frac{2y}{(x^2+y^2)^2}j\tag{5} gradz=−(x2+y2)22xi+−(x2+y2)22yj(5)
(x, y) = (1, 2),
g r a d z = − 2 25 i + − 4 25 j (6) grad{\,}z=-\frac{2}{25}i+-\frac{4}{25}j\tag{6} gradz=−252i+−254j(6)
即点(1, 2)位置函数值下降最快的方向为(-2/25, -4/25)。
(x, y) = (3, 4),
g r a d z = − 6 625 i + − 8 625 j (7) grad{\,}z=-\frac{6}{625}i+-\frac{8}{625}j\tag{7} gradz=−6256i+−6258j(7)
-
当(a, b) = (2, 2)时
g r a d z = − 4 x ( 2 x 2 + 2 y 2 ) 2 i + − 4 y ( 2 x 2 + 2 y 2 ) 2 j (8) grad{\,}z=-\frac{4x}{(2x^2+2y^2)^2}i+-\frac{4y}{(2x^2+2y^2)^2}j\tag{8} gradz=−(2x2+2y2)24xi+−(2x2+2y2)24yj(8)
(x, y) = (1, 2),
g r a d z = − 2 100 i + − 4 100 j (9) grad{\,}z=-\frac{2}{100}i+-\frac{4}{100}j\tag{9} gradz=−1002i+−1004j(9)
(x, y) = (3, 4),
g r a d z = − 12 2500 i + − 16 2500 j (10) grad{\,}z=-\frac{12}{2500}i+-\frac{16}{2500}j\tag{10} gradz=−250012i+−250016j(10) -
总结
从1. 2. 中可以看出,z上的不同点,其函数值下降最快的方向是不同的,其梯度为(x, y)的函数。
对于不同的(a, b),同样的位置(x, y)函数值下降最快的方向也是不同的。
以公式(6)为例,点(1, 2)位置函数值下降最快的方向为(-2/25, -4/25),如果想要降低函数值,在此点处可以向梯度方向走一定的距离,例如,选取0.1倍的梯度,即从位置(1, 2)移动到(1, 2) + 0.1 * (-2/25, -4/25) = (0.92, 1.84)
类比
将数学分析类比到深度学习模型,
输入数据为(a, b);模型只有1层,参数为x, y;损失函数z为包含a,b,x,y的函数;(模型输出应该也为包含a,b,x,y的函数,但不予考虑)
训练目的即降低损失函数z的值,采用梯度下降法。
这里类比的根据为输入数据(a, b)值不可变;模型对输入数据进行相应运算并输出,相应运算即包含不同的参数,这些参数变量会在训练的过程中不断的更新;根据输出和GT值定义损失函数,损失函数为与 输入值和参数值 相关的函数(函数z)。
梯度下降法有 批量梯度下降法(BGD)、随机梯度下降法(SGD)和小批量梯度下降法(MBGD)三种,其区别的本质在于损失函数定义的区别:
1) 数学分析中所使用的是SGD,其每次迭代使用一个样本对参数进行更新,即每输入一个确定值(a0, b0),损失函数及其偏导则成为(x, y)的函数,对当前的(x, y)值沿梯度方向更新即可。类比中提到的0.1倍梯度,为更新的幅度,称为学习率。
2) BGD的损失函数定义,每次迭代使用所有样本对参数进行更新,对所以样本的损失求一个平均值,假设我们一共有3个样本(a0, b0),(a1, b1),(a2, b2),损失函数将定义为
z = 1 a 0 x 2 + b 0 y 2 + 1 a 1 x 2 + b 1 y 2 + 1 a 2 x 2 + b 2 y 2 3 z=\frac{\frac{1}{a_0x^2+b_0y^2}+\frac{1}{a_1x^2+b_1y^2}+\frac{1}{a_2x^2+b_2y^2}}{3} z=3a0x2+b0y21+a1x2+b1y21+a2x2+b2y21
接下来,对改公式进行求梯度,然后对当前的(x, y)值沿梯度方向更新即可。
3)MBGD的损失函数定义,每次迭代使用一部分样本对参数进行更新,对这部分样本的损失求一个平均值,假设我们拿出3个样本(a0, b0),(a1, b1),(a2, b2),损失函数将定义为
z = 1 a 0 x 2 + b 0 y 2 + 1 a 1 x 2 + b 1 y 2 + 1 a 2 x 2 + b 2 y 2 3 z=\frac{\frac{1}{a_0x^2+b_0y^2}+\frac{1}{a_1x^2+b_1y^2}+\frac{1}{a_2x^2+b_2y^2}}{3} z=3a0x2+b0y21+a1x2+b1y21+a2x2+b2y21
接下来,对改公式进行求梯度,然后对当前的(x, y)值沿梯度方向更新即可。
推广
1. 链式求导法则
数学分析和类比中所提及的是网络模型极其简单的情况,将其推广到一般情况为:
输入为x,其可能为向量或者矩阵;
多层网络,每层将对上一层的输出进行操作,可以看做函数嵌套过程,第一层f(x),第二层g(f(x)),第三层t(g(f(x))),…,每一层函数都包含大量的参数,例如g(.)层参数为g0,g1,…gm;
损失函数为与x和各层参数相关的函数;
根据嵌套函数的链式求导法则,可以求得损失函数对于某一层所有参数的偏导,以及对该层参数的梯度,下面的操作则与数学分析和类比中类似,将该层的参数向着其梯度的方向更新即可。对于一次的数据输入,先对后面的层求梯度,更新,然后不断向前,直至对第一层进行求梯度,参数更新。
2. BGD、SGD、MBGD优缺点
1)BGD
优点:
(1)一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
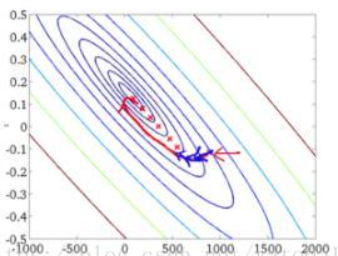
(2)由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点:
(1)当样本数目 m 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。
2)SGD
优点:
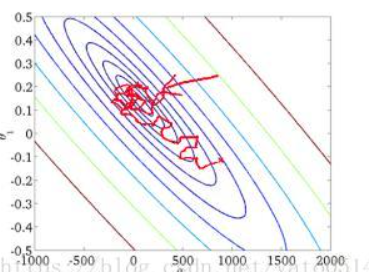
(1)由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
(1)准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
(2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
(3)不易于并行实现。
3)MBGD(BGD和SGD的折中方案)
优点:
(1)通过矩阵运算,每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
(2)每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。(比如样本30W,设置batch_size=100时,需要迭代3000次,远小于SGD的30W次)
(3)可实现并行化。
缺点:
(1)batch_size的不当选择可能会带来一些问题。
