优化算法optimization：SGD动量法momentum

动量法

提出动机

在SGD的每次迭代中，梯度下降根据自变量当前位置，沿着当前位置的梯度更新自变量。然而，如果自变量的迭代方向仅仅取决于自变量当前位置可能会带来一些问题。

我们考虑一个二维输入向量$x=[x_1,x_2{]}^T$和目标函数$f(x)=0.1x_1^2+2x_2^2$。

import numpy as np
import matplotlib.pyplot as plt

# 目标函数
def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2

# 目标函数的梯度
def gd_2d(x1, x2, s1, s2, eta=0.4):
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

# x参数为起始位置，s是自变量状态
def train_2d(trainer, iters=20, x1=-5, x2=-2, s1=0, s2=0): 
    results = [(x1, x2)]
    for i in range(iters):
        x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
    print('epoch {}, x1 {}, x2 {}'.format(i+1, x1, x2))
    return results

# 梯度下降过程
def show_trace_2d(f, results, xrange=np.arange(-5.5, 1.0, 0.1), yrange=np.arange(-3.0, 2.0, 0.1)):  
    plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = np.meshgrid(xrange, yrange)
    plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    plt.xlabel('x1')
    plt.ylabel('x2')

利用如下代码画出运行轨迹。

show_trace_2d(f_2d, train_2d(gd_2d))

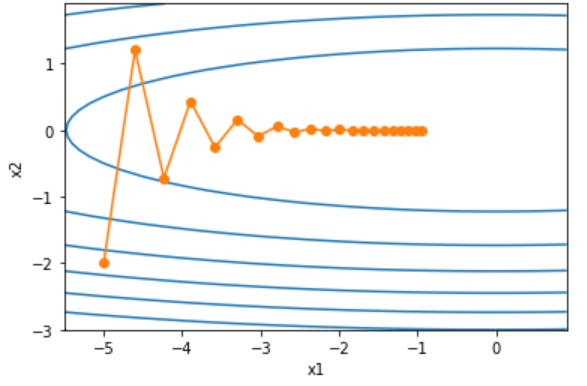
我们发现，最开始的几次迭代在梯度陡峭的方向进行较大的更新，但是这种震荡恰恰是我们不太需要的。我们更希望向梯度较为平缓的方向进行更新。如果调大学习率，在梯度较为平缓的方向进行的更新确实会增大，但是也可能导致参数最后没有收敛到最优解。

动量法

我们定义动量超参数$\gamma$，范围是$[0,1)$。取零时，等同于小批量随机梯度下降。在时间步$t$的小批量随机梯度为$g_t$，学习率是${\eta }_t$。对每次迭代做如下改动
$$\begin{gathered} v_t=\gamma v_{t-1}+{\eta }_t{g}_t \\ {x}_t=x_{t-1}-v_t \end{gathered}$$
利用代码画出更新过程。

def momentum_2d(x1, x2, v1, v2, eta=0.4, gamma=0.5):
    v1 = gamma * v1 + eta * 0.2 * x1 ## 此处导数是硬编码
    v2 = gamma * v2 + eta * 4 * x2 ## 此处导数是硬编码
    return x1 - v1, x2 - v2, v1, v2

show_trace_2d(f_2d, train_2d(momentum_2d))

我们发现轨迹在上下方向的振幅减小了，而且更快收敛到了最优解。

指数加权移动平均

学过时间序列的同学可能对加权移动平均非常熟悉。当前时间步$t$的变量$y_t$是上一时间步改变量的值和当前时间步另一变量$x_t$的线性组合。
$$y_t=\gamma y_{t-1}+(1-\gamma )x_t$$
如果我们将这个通项公式进行展开，
$$\begin{gathered} y_t=(1-\gamma )x_t+\gamma y_{t-1} \\ =(1-\gamma )x_t+(1-\gamma )\gamma x_{t-1}+{\gamma }^2{y}_{t-2} \\ =(1-\gamma )x_t+(1-\gamma )\gamma x_{t-1}+(1-\gamma ){\gamma }^2{x}_{t-2}+{\gamma }^3{y}_{t-3} \\ .... \end{gathered}$$
令$n=1/(1-\gamma )$，可以得到
$$(1-\frac{1}{n}{)}^n={\gamma }^{\frac{1}{1-\gamma }}$$
我们知道
$$li{m}_{n\to \infty }(1-\frac{1}{n}{)}^n=exp(-1)\approx 0.3679$$
所以，当$\gamma \to 1$时，${\gamma }^{\frac{1}{1-\gamma }}=exp(-1)$。我们可以将$exp(-1)$当成一个很小的数，从而在通项公式展开中忽略带有这一项（或者更高阶）的系数的项。因此，在实际中，我们常常将$y_t$看成是对最近$\frac{1}{1-\gamma }$个时间步的$x_t$值的加权平均。距离当前时间步$t$越近的$x_t$值获得的权重越大（越接近1）。

我们可以对动量法的速度变量做变形。
$$v_t=\gamma v_{t-1}+(1-\gamma )(\frac{{\eta }_t}{1-\gamma }{g}_t)$$
由指数加权移动平均的形式可得，速度变量$v_t$实际上对序列$\frac{{\eta }_t}{1-\gamma }{g}_t$做了指数加权移动平均。动量法在每个时间步的自变量更新量近似于将前者对应的最近$1/(1-\gamma )$个时间步的更新量做了指数加权移动平均后再除以$1-\gamma$。所以，在动量法中，自变量在各个方向上的移动幅度不仅取决于当前梯度，还取决于过去的各个梯度在各个方向上是否一致。如果一致，则会加速，使自变量向最优解更快移动。

代码实现

def init_momentum_states(dim=2):
    v_w = np.zeros((dim, 1))
    v_b = np.zeros(1)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        v[:] = hyperparams['momentum'] * v + hyperparams['lr'] * p.grad
        p[:] -= v

Reference

• Dive Into Deep Learning，第7章