在数据建模时,经常会用到多元高斯分布模型,下面就这个模型的公式并结合它的几何意义,来做一个直观上的讲解。
1, 标准高斯函数
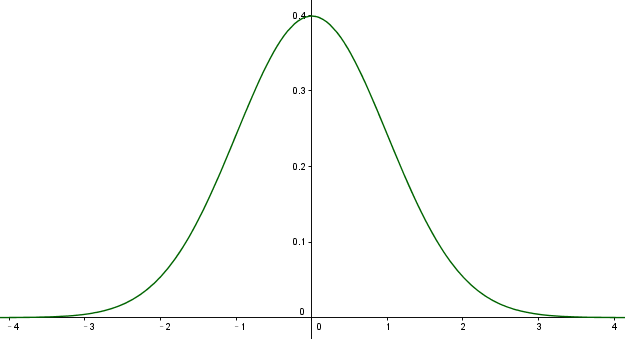
高斯函数标准型:
$f(x) = \frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}}$
这个函数描述了变量 x 的一种分布特性,变量x的分布有如下特点:
Ⅰ, 均值 = 0
Ⅱ, 方差为1
Ⅲ, 概率密度和为1
2, 一元高斯函数一般形式
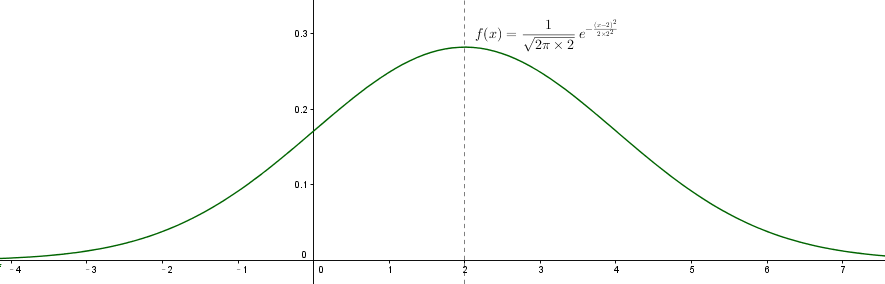
一元高斯函数一般形式:
$f(x) = \frac{1}{\sqrt{2π}σ}e^{-\frac{(x-μ)^2}{2σ^{2}}}$
我们可以令:
$z = \frac{x - μ}{σ}$
称这个过程为标准化, 不难理解,$z ∼ N(0, 1)$,从z -> x的过程如下:
Ⅰ, 将 x 向右移动 μ 个单位
Ⅱ, 将密度函数伸展 σ 倍
而标准化(x -> z)所做的事情就是上述步骤的逆向
唯一不太好理解的是前面 $\frac{1}{\sqrt{2π}σ}$ 中的σ, 为什么这里多了一个 σ, 不是 2σ 或其他?
当然,这里可以拿着概率密度函数的性质,使用微积分进行积分,为了保证最终的积分等于1, 这里必须是 σ
这里我想说一下自己的直观感受:
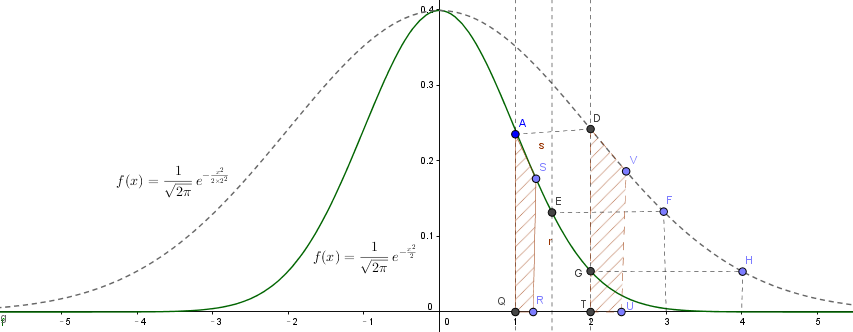
实线代表的函数是标准高斯函数:
$f(x) = \frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2×2^{2}}}$
虚线代表的是标准高斯函数在 x 轴方向2倍延展,效果如下:
A(x = 1) -> D(x = 2)
E(x = 1.5) -> F(x = 3)
G(x = 2) -> H(x = 4)
横向拓宽了,纵向还是保持不变,可以想象,最后的函数积分肯定不等于1
采用极限的思想,将 x 轴切分成无穷个细小的片段,每个片段可以与函数围城一个区域,因为我的切分足够小,这个区域的面积可以近似采用公式:面积 = 底 × 高 求得:
从 AQRS -> DTUV, 底乘以2倍,高维持不变,所以,要保持变化前后面积不变,函数的高度应该变为原来的 1/2
所以高斯函数在 x 轴方向做2倍延展的同时,纵向应该压缩为原来的一半,才能重新形成新的高斯分布函数
扩展到一般情形,x 轴方向做 σ 倍延拓的同时, y 轴应该压缩 σ 倍(乘以 1/σ)
3, 独立多元正态分布
先假设n个变量 $x = \left[ \begin{matrix} x_{1}, x_{2},\cdots,x_{n}\end{matrix}\right]^\mathrm{T}$ 互不相关,且服从正态分布(维度不相关多元正态分布),各个维度的均值$E(x) = \left[ \begin{matrix} μ_{1}, μ_{2},\cdots,μ_{n}\end{matrix}\right]^\mathrm{T}$, 方差 $σ(x) = \left[ \begin{matrix} σ_{1}, σ_{2},\cdots,σ_{n}\end{matrix}\right]^\mathrm{T}$
根据联合概率密度公式:
$f(x) = p(x_{1},x_{2}....x_{n}) = p(x_{1})p(x_{2})....p(x_{n}) = \frac{1}{(\sqrt{2π})^nσ_{1}σ_{2}\cdotsσ_{n}}e^{-\frac{(x_{1}-μ_{1})^2}{2σ_{1}^2}-\frac{(x_{2}-μ_{2})^2}{2σ_{2}^2}\cdots-\frac{(x_{n}-μ_{n})^2}{2σ_{n}^2}}$
令 $z^{2} = \frac{(x_{1}-μ_{1})^2}{σ_{1}^2}+\frac{(x_{2}-μ_{2})^2}{σ_{2}^2}\cdots+\frac{(x_{n}-μ_{n})^2}{σ_{n}^2}$, $σ_{z}= σ_{1}σ_{2}\cdotsσ_{n}$
这样多元正态分布又可以写成一元那种漂亮的形式了(注意一元与多元的差别):
$f(z) = \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2σ_{z}^2}}$
因为多元正态分布有着很强的几何思想,单纯从代数的角度看待z很难看出z的概率分布规律,这里需要转换成矩阵形式:
$z^2 = z^\mathrm{T}z = \left[ \begin{matrix} x_{1} - μ_{1}, x_{2} - μ_{2}, \cdots,x_{n} - μ_{n}\end{matrix}\right] \left[ \begin{matrix} \frac{1}{σ_{1}^2}&0&\cdots&0\\
0&\frac{1}{σ_{2}^2}&\cdots&0\\
\vdots&\cdots&\cdots&\vdots\\
0&0&\cdots&\frac{1}{σ_{n}^2}
\end{matrix}\right]\left[ \begin{matrix} x_{1} - μ_{1}, x_{2} - μ_{2}, \cdots,x_{n} - μ_{n}\end{matrix}\right]^\mathrm{T}$
等式比较长,让我们要做一下变量替换:
$x - μ_{x} = \left[ \begin{matrix} x_{1} - μ_{1}, x_{2} - μ_{2}, \cdots,x_{n} - μ_{n}\end{matrix}\right]^\mathrm{T}$
定义一个符号
$∑_{}^{} = \left[ \begin{matrix} σ_{1}^2&0&\cdots&0\\
0&σ_{2}^2&\cdots&0\\
\vdots&\cdots&\cdots&\vdots\\
0&0&\cdots&σ_{n}^2
\end{matrix}\right]$
$∑_{}^{}$代表变量 X 的协方差矩阵, i行j列的元素值表示$x_{i}$与$x_{j}$的协方差
因为现在变量之间是相互独立的,所以只有对角线上 (i = j)存在元素,其他地方都等于0,且$x_{i}$与它本身的协方差就等于方差
$∑_{}^{}$是一个对角阵,根据对角矩阵的性质,它的逆矩阵:
$( (∑_{}^{})^{-1} = \left[ \begin{matrix} \frac{1}{σ_{1}^2}&0&\cdots&0\\
0&\frac{1}{σ_{2}^2}&\cdots&0\\
\vdots&\cdots&\cdots&\vdots\\
0&0&\cdots&\frac{1}{σ_{n}^2}
\end{matrix}\right]$
对角矩阵的行列式 = 对角元素的乘积
$σ_{z}= \left|∑_{}^{}\right|^\frac{1}{2} =σ_{1}σ_{2}.....σ_{n}$
替换变量之后,等式可以简化为:
$z^\mathrm{T}z = (x - μ_{x})^\mathrm{T} \sum_{}{}^{-1} (x - μ_{x})$
代入以z为自变量的标准高斯分布函数中:
$f(z) = \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}} = \frac{1}{(\sqrt{2π})^{n}\left|∑_{}^{}\right|^\frac{1}{2}}e^{-\frac{ (x\ -\ μ_{x})^\mathrm{T}\ (\sum_{}{})^{-1}\ (x\ -\ μ_{x})}{2}}$
注意前面的系数变化:从非标准正态分布->标准正态分布需要将概率密度函数的高度压缩 $|∑_{}^{}|^\frac{1}{2}$倍, 从一维 -> n维的过程中,每增加一维,高度将压缩 $\sqrt{2π}$倍
维度不相关正太分布函数图像类似这样(以二元分布函数为例):
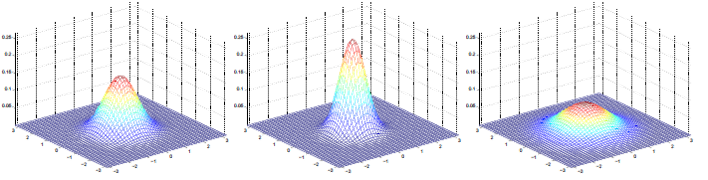
4, 相关多元正态分布
前面也说了,我们讨论多元正态分布的前提是多元变量之间是相互独立的,实际上,有很多应用场合,变量与变量之间是有关联的。以二元正态分布为例:
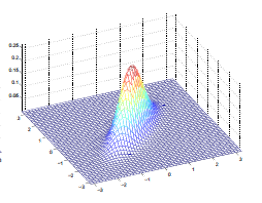
向输入平面作投影后的平面图:

以现在的坐标系来看,X1,X2是相关的,但是如果我们换一个角度,它们就是互不相关的了:

上述过程被称为去相关性,更专业一点叫做归化
假设新坐标系 $x_{1}' = \left[\begin{matrix}u_{x1}^{0}, u_{x1}^{1}\end{matrix}\right]^T$, $x_{2}' = \left[\begin{matrix}u_{x2}^{0}, u_{x2}^{1}\end{matrix}\right]^T$那么原坐标系上的任意一点 $[x_{1}, x_{2}]^T$ 投影到新坐标系上的结果为:
$\left[\begin{matrix}x_{1}'\\
x_{2}'\end{matrix}\right] = \left[ \begin{matrix} u_{x1}^{0}, u_{x1}^{1}\\
u_{x2}^{0}, u_{x2}^{1} \end{matrix} \right]\left[ \begin{matrix} x_{1}\\
x_{2} \end{matrix} \right]$
为了简单起见,定义矩阵:
$U = \left[ \begin{matrix} u_{x1}^{0}, u_{x2}^{0}\\
u_{x1}^{1}, u_{x2}^{1} \end{matrix} \right]$
U的列空间由新坐标向量组成,坐标映射之后:
$X’ = U^{T}X$
现在我们的自变量X’是相互独立的了,满足维度不相关高斯分布模型,现在我们想套用公式:
$f(z) = \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}} = \frac{1}{(\sqrt{2π})^{n}\left|∑_{}^{}\right|^\frac{1}{2}}e^{-\frac{ (x\ -\ μ_{x})^\mathrm{T}\ (\sum_{}{})^{-1}\ (x\ -\ μ_{x})}{2}}$
$x->x'$, 这个很容易,$μ_{x} -> μ(x')$这个也不难, 但是这里还有一个 $∑_{}^{}$是未知的! 按照定义,这里的$∑_{}^{}$应该是X’的协方差,我们已知X,已知映射矩阵,如何求解X’的协方差?
从定义出发:
$μ_{x'} = E[U^TX] = U^TE[x] = U^Tμ_{x}$ $\tag{$1$}$
映射之后的协方差:
$\begin{align*}
σ(X') &= E[(X' - μ_{X'})(X' - μ_{X'})^T]\\
&=E[ (X' - μ_{X'}) (X'^T - μ_{X'}^T) ]\\
&=E[X'X'^T - μ_{X'}X'^T - X'μ_{X'}^T + μ_{X'}μ_{X'}^T]\\
&=E[U^TXX^TU-E[U^TX]X^TU - U^TXE[U^TX]^T + E[U^TX]E[U^TX]^T]\\
&=U^TE[XX^T - E(X)X^T - XE[X]^T + E[X]E[X]^T]U\\
&=U^Tσ(X)U\\
\end{align*}$
坐标映射前后的协方差矩阵满足关系:
$(\sum_{}^{})_{x'} = U^{T}(\sum_{}^{})_{x}U$ $\tag{$2$}$
再进一步观察,U的列向量是单位向量,而且是相互正交的,U是正交矩阵,$U^T = U^{-1}$
$(\sum_{}^{})_{x'} = U^{-1}(\sum_{}^{})_{x}U$
也就是说$(\sum_{}^{})_{x'}$ 是 $(\sum_{}^{})_{x}$的相似矩阵,相似矩阵的行列式相等
$|(\sum_{}^{})_{x'}| = |(\sum_{}^{})_{x}|$ $\tag{$3$}$
并且还有一个重要结论:
$(\sum_{}^{})_{x'}^{-1} = (U^T(\sum_{}^{})_{x}U)^{-1} = (U^{-1}(\sum_{}^{})_{x}U)^{-1}=U^{-1}(\sum_{}^{})_{x}^{-1}U = U^{T}(\sum_{}^{})_{x}^{-1}U$ $\tag{$4$}$
有了上述1、2、3、4四个结论,我们就可以放心套用标准化公式了:
$\begin{align*}
f(z) &= \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}} \\
&= \frac{1}{(\sqrt{2π})^{n}\left|(∑_{}^{})'_{x}\right|^\frac{1}{2}}e^{-\frac{ (x'\ -\ μ_{x'})^\mathrm{T}\ (\sum_{}{})_{x'}^{-1}\ (x'\ -\ μ_{x'})}{2}}\\
&=\frac{1}{(\sqrt{2π})^{n}\left|(∑_{}^{})_{x}\right|^\frac{1}{2}}e^{-\frac{ (U^Tx\ -\ U^Tμ_{x})^\mathrm{T}\ U^T (\sum_{}{})_{x}^{-1}\ U (U^Tx\ -\ U^Tμ_{x})}{2}}\\
&=\frac{1}{(\sqrt{2π})^{n}\left|(∑_{}^{})_{x}\right|^\frac{1}{2}}e^{-\frac{ (x\ -\ μ_{x})^\mathrm{T}\ (\sum_{}{})_{x}^{-1}\ (x\ -\ μ_{x})}{2}}
\end{align*}$
总结一下我们做了什么。
Ⅰ, 我们先定义了新的坐标系,通过矩阵 $U^{T}$ 将元素映射到新的坐标系,目的是去相关性
Ⅱ, 在新的坐标下,我们定义了新的期望、协方差、协方差的逆,他们都可以通过 $U$ 与 $U^T$计算出来,当然我们不用计算
Ⅲ, 套用标准公式,将新的期望、协方差的逆、协方差的行列式代入,发现最后的结果与$U$、$U^T$无关
为什么会这样?我的理解是这样:
前提条件:概率模型已经构建

假设空白平面上有一点A, 这个点A是客观存在的,一旦A指定了,那么它的概率大小P(A)就已经确定了

现在我们添加了一个坐标系,添加坐标系的好处只是使得P(A)可以被量化 $P(A) = f(u1, u2)$
同理,使用其他坐标系,可以得到其他坐标系下的另外一种量化 $P(A) = f(v1, v2)$
不管使用哪个坐标系,A点的概率始终是不变的,所以$f(u1, u2) = f(v1, v2)$(感觉这有点像哲学问题哈)。
5, 实例分析
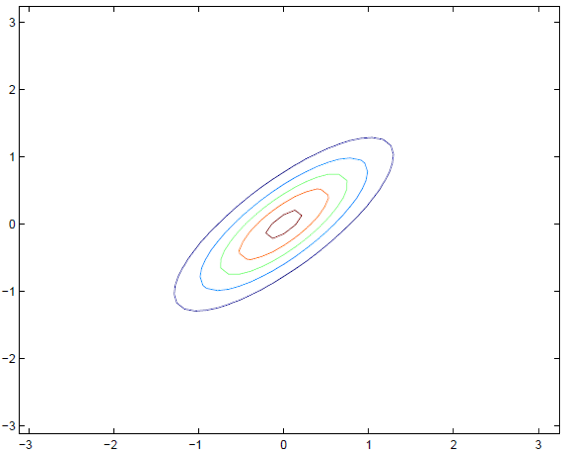
$\sum_{}^{} = \left[ \begin{matrix} 1&0.8\\
0.8&1
\end{matrix} \right]$
这个图形与参数是如何对应的?
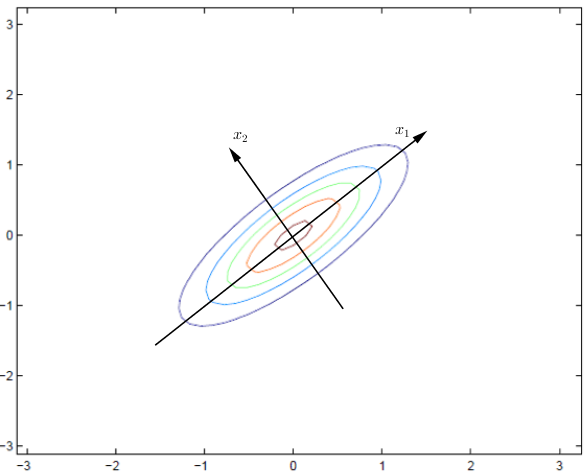
可以把那条假象的坐标轴线画出来,转换前后,坐标原点不变,很明显,这是一个旋转变换,假设坐标轴旋转的角度为θ,新的坐标向量矩阵将变为:
$U = \left[ \begin{matrix} cosθ&-sinθ\\
sinθ&cosθ
\end{matrix}\right]$
U的列空间组成了新坐标的坐标系
$U^T = \left[ \begin{matrix} cosθ&sinθ\\
-sinθ&cosθ
\end{matrix}\right]$
新坐标系下变量是不相关的,协方差矩阵为对角阵:
$(\sum_{}^{})_{new} = U^T \sum{} U = \left[ \begin{matrix} cosθ&sinθ\\
-sinθ&cosθ
\end{matrix}\right] \left[ \begin{matrix}
1&0.8\\
0.8&1
\end{matrix} \right] \left[ \begin{matrix} cosθ&-sinθ\\
sinθ&cosθ
\end{matrix}\right] = \left[ \begin{matrix} σ_{1}^2&0\\
0&σ_{2}^2
\end{matrix} \right]$
计算可得: $θ = \frac{π}{4}$
代入计算新的协方差为:
$(\sum_{}^{})_{new} = \left[ \begin{matrix} 1.8&0\\
0&0.2 \end{matrix} \right]$
得出的结论: 新的坐标系是原坐标系经过 $θ = \frac{π}{4}$旋转而来,在新的坐标系下,输入元素将会变得不相关,$x_{1}$方向的方差为1.8,分布比较宽, $x_{2}$方向的方差为0.2,分布比较窄,整体表现为扁平。
同理,不难得出:
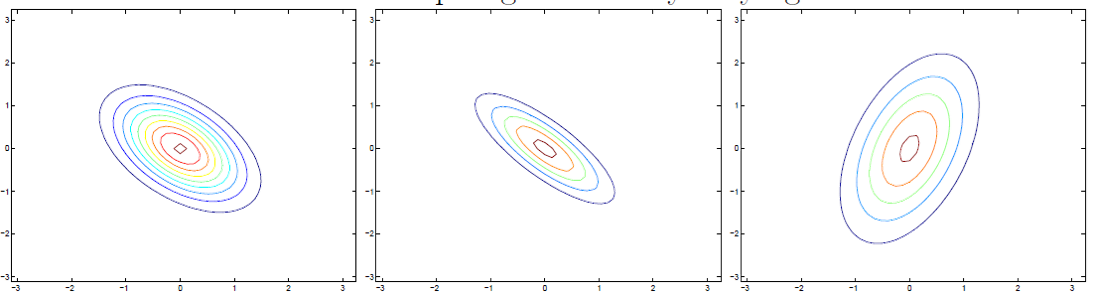
$\sum_{}^{} = \left[ \begin{matrix} 1&-0.5\\
-0.5&1
\end{matrix} \right]\qquad\qquad\qquad\qquad\sum_{}^{} = \left[ \begin{matrix} 1&-0.8\\
-0.8&1
\end{matrix} \right]\qquad\qquad\qquad\qquad\sum_{}^{} = \left[ \begin{matrix} 3&0.8\\
0.8&1
\end{matrix} \right]$
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
路漫漫其修远兮,吾将上下而求索