等和线与区域表示
0.前言
期中考前停课不小心给数学排了7节课……于是就有了这篇文章。

其实已经被这个问题困扰好久了,那天又翻到了当时猜出来的那道题。黄巨不吝赐教,送给我三个字——等和线。
回去玩了一下,发现自己列的不等式和所长给的解答是一致的。抱着水研究性学习的想法,就把它写出来了。
1.等和线
就是大家熟知的 P C ⃗ = λ P A ⃗ + μ P B ⃗ , λ + μ = 1 ⟺ A , B , C \vec{PC} =\lambda\vec{PA}+\mu\vec{PB},\lambda+\mu=1\iff A,B,C PC=λPA+μPB,λ+μ=1⟺A,B,C共线 这个大题目不能直接用的实用定理。
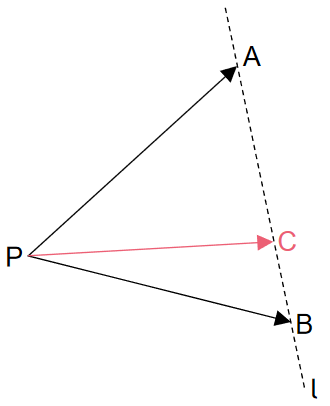
稍微推广一下,当 λ + μ \lambda+\mu λ+μ为定值时,C在定直线上。
这也很好理解,不妨设 λ + μ = m , P A ′ ⃗ = m P A ⃗ , P B ′ ⃗ = m P B ⃗ \lambda+\mu=m,\vec{PA'}=m\vec{PA},\vec{PB'}=m\vec{PB} λ+μ=m,PA′=mPA,PB′=mPB,则
P C ⃗ = λ P A ⃗ + μ P B ⃗ = λ m P A ′ ⃗ + μ m P B ′ ⃗ \vec{PC} =\lambda\vec{PA}+\mu\vec{PB}=\cfrac{\lambda}{m}\vec{PA'}+\cfrac{\mu}{m}\vec{PB'} PC=λPA+μPB=mλPA′+mμPB′,
而 λ m + μ m = 1 \cfrac{\lambda}{m}+\cfrac{\mu}{m}=1 mλ+mμ=1,故 A ′ , B ′ , C A',B',C A′,B′,C三点共线, C C C在直线 A ′ B ′ A'B' A′B′上。
大部分的文章会教你找 λ , μ \lambda,\mu λ,μ组成的线性式的最值,但我想和你谈谈 λ \lambda λ和 μ \mu μ之间的关系。

2.基本模型
我们的问题是确定选定基底数乘的系数,使这组基底可以表达出某个区域内的所有点。
更具体一点,对于曲边区域,其次数已经超过了一次,这超过了7节数学复习的范畴,等下次停课复习再做考虑。(考虑个鬼,建系它不香吗) 所以我们主要研究直线围成的区域。
直接研究也显得不甚方便,所以我们化大为小,先确认一个基本图形。
根据等和线模型的特点,我决定选择梯形。而三角形又可以看做特殊的梯形,而所有的凸多边形都可以被划分为若干个三角形,我们就可以写出绝大多数直线围成的区域了。
让我们先来看看基本模型:

好了,基本模型《看完了》,让我们先了解一下模型背后的原理。
为了刻画一个对象,我们需要选取适当的状态参量来描述它。对于一个二维平面区域,笛卡尔告诉我们只要两个参数就够了,比如(x,y)这样的数对,它的几何意义是沿着两个坐标轴分别前进x和y个单位。
类似的,从几何意义出发,我们来看一下这个模型。结合等和线结论,我们可以把域看作是一组平行线段的集合。但问题就出在这里,等和线描述的是直线,而我们要求的是线段。怎么办呢?
也好办。可以看到图上有分点,我们想做出一个“旋转”式的刻画:从 O A ⃗ \vec{OA} OA旋转至 O B ⃗ \vec{OB} OB,这样就有了对两个斜边边界的限制。但是问题又来了,上下的平行边界又能否兼顾呢?
显然可以。(不然7节数学白复习了) 我们回顾等和线的证明,其中有将两个基向量同时扩大相同倍数这一步骤。从另一个角度来看,这其实是将原来和基底共线的向量拉长了,即图中的 O P ⃗ \vec{OP} OP拉长至 O C ⃗ \vec{OC} OC.为了刻画这一步骤,我们引入距 λ \lambda λ,即 O C ⃗ = λ O P ⃗ \vec{OC}=\lambda\vec{OP} OC=λOP.
综合这两个步骤,我们可以给出区域内任一点的几何描述:“旋转”至分点,伸长至该点。而“旋转”其实并不是真正意义上的旋转,我们又可以将它看作基点指向等和线上的一点(即分点)。
在这样的原理上,我们来构建它的数学表达。
显然,我们可以将 O P ⃗ \vec{OP} OP写作 a O A ⃗ + ( 1 − a ) O B ⃗ a\vec{OA}+(1-a)\vec{OB} aOA+(1−a)OB(A,P,B共线),则
O C ⃗ = λ ( a O A ⃗ + ( 1 − a ) O B ⃗ ) \vec{OC}=\lambda(a\vec{OA}+(1-a)\vec{OB}) OC=λ(aOA+(1−a)OB)
由于这个式子中我们选定了 a , λ a,\lambda a,λ两个参数,故称之为 a − λ a-\lambda a−λ表示法。
回到我们最初的问题上来。我们的目的是为了给出 O A ⃗ \vec{OA} OA, O B ⃗ \vec{OB} OB数乘系数的关系,即 O C ⃗ = x O A ⃗ + y O B ⃗ \vec{OC}=x\vec{OA}+y\vec{OB} OC=xOA+yOB中x,y的关系。利用平面向量基本定理带入整理,可得
{ x + y = λ , y x = 1 a − 1. ( a = 0 这 种 细 节 自 己 讨 论 去 ) \left\{ \begin{array}{lr} x+y=\lambda,\\ \cfrac{y}{x}=\cfrac{1}{a}-1.(a=0这种细节自己讨论去) \end{array} \right. ⎩⎨⎧x+y=λ,xy=a1−1.(a=0这种细节自己讨论去)
这就给出了x,y之间的关系。
但我们还需要确认参数 a , λ a,\lambda a,λ的范围。不难发现,每个状态都是随着参数的变化连续变化的,而且每一个参数对应的状态都是唯一的,所以我们只需确定每个参数的起始取值即可。
对于参数 λ \lambda λ,利用定义就可以确定其取值,即 λ = ∣ O C ⃗ ∣ ∣ O P ⃗ ∣ \lambda=\cfrac{|\vec{OC}|}{|\vec{OP}|} λ=∣OP∣∣OC∣.
对于参数a,利用定比分点公式,如果有 A P ⃗ = m P B ⃗ \vec{AP}=m\vec{PB} AP=mPB,则 a = 1 1 + m a=\cfrac{1}{1+m} a=1+m1.
这样,我们就可以表达出这个区域里所有的点了。
3.基本模型的组合
原理很简单,就是选定区域内一点,分别在每个划分区域里表达基本模型。
例如平行四边形区域:
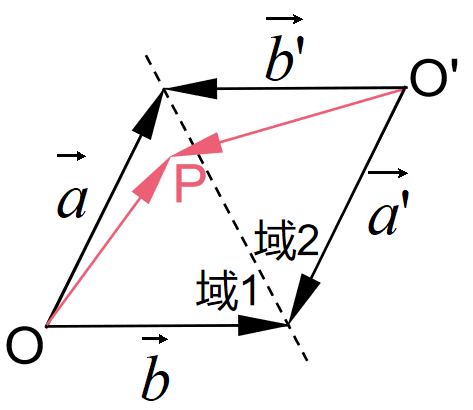
很明显,我们可以将它拆成两个三角形来处理。
先设 O P ⃗ = x a ⃗ + y b ⃗ \vec{OP}=x\vec{a}+y\vec{b} OP=xa+yb,我们要求x,y之间的关系。
对于域1,我们容易确定 ( a , λ ) = ( [ 0 , 1 ] , [ 0 , 1 ] ) (a,\lambda)=([0,1],[0,1]) (a,λ)=([0,1],[0,1]),即有
{ x + y ∈ [ 0 , 1 ] , y x ∈ [ 0 , + ∞ ) . \left\{ \begin{array}{lr} x+y\in[0,1],\\ \cfrac{y}{x}\in[0,+\infty). \end{array} \right. ⎩⎨⎧x+y∈[0,1],xy∈[0,+∞).
对于域2,我们同样可以确定 ( a , λ ) = ( [ 0 , 1 ] , [ 0 , 1 ] ) (a,\lambda)=([0,1],[0,1]) (a,λ)=([0,1],[0,1]),只是这是的基向量和用于表示的向量发生了变化。
不难看出, a ′ ⃗ = − a ⃗ \vec{a'}=-\vec{a} a′=−a, b ′ ⃗ = − b ⃗ \vec{b'}=-\vec{b} b′=−b,
O ′ P ⃗ = O P ⃗ − O O ′ ⃗ = O P ⃗ − ( a ⃗ + b ⃗ ) = ( x a ⃗ + y b ⃗ ) − ( a ⃗ + b ⃗ ) = ( x − 1 ) a ⃗ + ( y − 1 ) b ⃗ = ( 1 − x ) a ′ ⃗ + ( 1 − y ) b ′ ⃗ \vec{O'P}=\vec{OP}-\vec{OO'}\\=\vec{OP}-(\vec{a}+\vec{b})=(x\vec{a}+y\vec{b})-(\vec{a}+\vec{b})\\=(x-1)\vec{a}+(y-1)\vec{b}=(1-x)\vec{a'}+(1-y)\vec{b'} O′P=OP−OO′=OP−(a+b)=(xa+yb)−(a+b)=(x−1)a+(y−1)b=(1−x)a′+(1−y)b′
故 x ′ = 1 − x , y ′ = 1 − y x'=1-x,y'=1-y x′=1−x,y′=1−y,即有
{ ( 1 − x ) + ( 1 − y ) ∈ [ 0 , 1 ] , 1 − y 1 − x ∈ [ 0 , + ∞ ) . \left\{ \begin{array}{lr} (1-x)+(1-y)\in[0,1],\\ \cfrac{1-y}{1-x}\in[0,+\infty). \end{array} \right. ⎩⎨⎧(1−x)+(1−y)∈[0,1],1−x1−y∈[0,+∞).
两者取并集,即为整个域的表达,即 0 ≤ x ≤ 1 且 0 ≤ y ≤ 1 0\le x\le1且0\le y\le1 0≤x≤1且0≤y≤1.
总结一下,总共分三步走,先表示用于表示域的向量,再将该向量表示为任意基底的分解,再将目标基底表示这组基底。
至于能否成功组合,就要看各位向量运算的基本功了。

这篇文章到这里基本上就要开始升华主题了。
最近在读村上,他的“孤独”说给人以很大冲击,其对“虚空”的品味,颇有佛性的释然。人生如此,高三生活亦如此。一轮复习仅仅是知识的重复吗?高三学生仅仅是作业的奴隶吗?在“知识孤独”的困境里,基于“学科素养”又不为其局限的小探究,往往成就激流中的小小感动。
毕竟,空即是色。
这篇文章到这里就结束了,如果有什么问题,欢迎在评论区讨论。