梯度下降算法广泛应用于寻找多变量函数的最小值,但是在神经网络的世界中,由基本函数表示的变量,参数,和函数的关系错综复杂,求解梯度并不是一件容易的事情,无法直接使用梯度下降算法。于是研究这一块儿的专家就研究出了一种误差反向传播法,根据计算流的拓扑关系,即可推导出每一层的误差情况,为了便于自己学和理解,这里我以一个网络为例,来说明这个算法的计算过程的细节。
网络拓扑结构图如下:

先看正向传播:
再来看反向传播:
由于
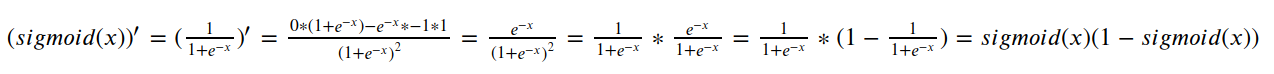
所以:
所以:
最后一部,要找源头的导数了:
所以:
所以:
所以:
=
通过上面的公式,我们来看反向传播的反向是什么意思?
上述公式的三个部分正好对应的正好是反向传播对应的下面三个阶段。

基于上图,我们扩展多个输出会怎样?

当有多个输出的时候,问题一下子变得复杂起来,每个都对
的改变有自己的想法,这个时候该怎么办呢?
兵来将挡,水来土掩,方法是把对每个
的想法按照列向量的方式排列,最后加起来,作为总的想法,更新权重向量的值.
所以,根据全微分法则:
最终的调整梯度为针对每个的梯度列向量的和:
再来看看反向传播矩阵转置的规则
所以:
另外针对的导数:
所以:
再加上前面的推导结论:
我们可以得出反向传播的两个公式,这两个公式对理解反向传播的代码非常重要,它将繁杂的导数计算替换为数列的递推关系式,这里用x代替h.
而在递推关系中,起到衔接两个递推式的枢纽计算,就是
在有些书中,这个式子被记为:
被叫做是神经元误差。
将神经元误差带入上式,可以得到:
所以,反向传播的计算可以转换为矩阵相乘的形式,这就为神经网络梯度的反向传播软件实现提供了统一的形式,因为计算机不擅长导数计算,但是擅长处理数值计算和递推,以上的式子可以通过递推
可以看出,正向传递和反向传递的权重该矩阵是互相转置的,权重矩阵的梯度可以通过输出和输入来表示:
比如MxN维矩阵和Nx1维矩阵相乘,得到Mx1维的向量,而Mx1维的向量和转置后的1xN维的向量相乘,可以返回MxN维的矩阵梯度维数信息,也就是说,维度不会丢失。
下面的推导是错误记录,有的时候,明白自己所犯错误的原因比明白问题本身更重要。
这个推导之所以错误从形式上也可以看出,由于最后一层是全连接,E对w11的偏导数不应该只和y1有关,还应该和其余的y2 .... yj....yk都有关,也不知道一开始为什么自己会这样想。
这样,求出每个对
的导数之后,将这些所有梯度加起来,作为最终梯度,去调整
,得到的就是新的一组权重值,调整后的参数比之前更加接近于训练目标想要达到的功能。


反向传播 Back Propagation (手把手推导)_哔哩哔哩_bilibili