在这个世界上存在的现象大体分为必然现象和随机现象两类。必然现象就像太阳每天必然从东边升起,西边落下那样,在相同条件下完全可以事先预测到它的结果。随机现象则不同,它在个别试验中会呈现不确定的结果,比如抛掷一次硬币,可能是正面,也可能是反面,不过在相同的条件下大量重复试验中又会呈现一定的规律性,因为当抛掷的次数逐渐增多时,出现正面或者反面的频率会逐渐接近 50%。
很显然,股票的涨跌属于随机现象,因为没有人能确定明天的具体走势。人们普遍对于不确定性存在恐惧,于是用一个介于 0 与 1 之间的数值来表示各个随机现象发生的可能性,这个数值就是概率。概率可以辅助人们对于未知结果作出理性的判断,量化交易的精髓正是如此,它从历史数据中得到大概率下获利的交易策略。
股市波动的规律一直是一个极具挑战性的世界级难题, 迄今为止已经出现过多个具有代表性的理论,随机漫步理论 (Random Walk Theory) 就是其中之一。随机漫步理论描述的正是股票涨跌的概率。早在 1990 年,巴黎一位博士生路易斯·巴舍利耶(1887—1946)跟踪当时巴黎股市起伏,期望用数学工具来描述股价变动过程。在他的论文《投机理论》中指出,股票价格的日常变动从根本上说是不可预知的,类似于“布朗运动”那样属于随机游走,没有任何规律可循。就好比一个人购买一只股票后立即将其卖掉,那么他输赢的概率是相等的。
理论中对于随机漫步现象解释到:由于流入市场的股票信息是公开的,市场中成千上万的专业人士会对股票进行详细的分析,驱动着股票多空交易,因此股票当前的价格实际已经反映了供求关系和内在的价值,而这个价格正是专业人士经过分析后所构成的一个合理价位,后续的市价会围绕着它上下波动。引起波动的原因会是新的经济、政治新闻、收购、合并、加息减息等等,这些消息是没有任何轨迹可循地流入市场,使得专业人士重新分析股票的价值,给出买卖方针,致使股票发生新的变化。由此可见,股票现时是没有记忆系统的,过去、现在和未来的涨跌并无关联,企图用股价的波动找出一个原理去预知股市去向是行不通的。随机漫步理论对技术图表派无疑是一个正面大敌,虽然理论至今仍然在经受着时间的检验,但如果理论一旦成立,所有股票专家都无立足之地。
不少专家学者都对随机漫步的论调有过研究,在《漫步华尔街》一书中提到了一个例子,作者让他的学生用抛硬币的方式构建一个假想的股价走势图。股价开始时定为 50 美元,此后每个交易日的收盘价右抛硬币的结果来确定:若抛出正面朝上便假定股票当天收盘价较前一天上涨 0.5%,反之则下跌 0.5%。最后根据随机抛硬币画出的走势图居然和正常的股价走势图非常相似,有“头肩顶”形态,甚至还呈现周期性的变动。
事实上股票价格真的就无法预测了吗?人生苦短,我们不妨用 Python 来探究下其中的奥秘。
2. Python 随机数的生成
Python 内置的 random 模块和第三方库 NumPy 的 random 模块都提供了生成随机漫步序列的方法,分别为 random.randint() 和 numpy.random.randint() 函数。NumPy 中主要以 N 维数组对象 ndarray 存储数据的,ndarray 作为 NumPy 的核心,不仅具有矢量算术运算的能力,并且在处理多维的大规模数组时快速且节省空间。
我们先了解下 ndarray 在效率方面的优势,通过对比 numpy.random.randint() 方法生成 1000000 个规模的随机数组和 random.randint() 方法生成一个等价的 Python 列表,以此来了解下它们之间具体的性能差距。实现代码如下所示:
def list_test():
walk = []
for _ in range(1000000):
walk.append(random.randint(0, 1))
def ndarray_test():
np.random.randint(0, 2, size=1000000)
t1 = timeit('list_test()', 'from __main__ import list_test', number=1)
t2 = timeit('ndarray_test()', 'from __main__ import ndarray_test', number=1)
print("list:{}".format(t1)) # list:1.3908312620000003
print("ndarray:{}".format(t2)) # ndarray:0.009495778999999871可见 NumPy 的 random 模块效率优势非常明显,基本是 Python 内置模块 random 的 100 倍以上,因此此处推荐使用 numpy.random.randint() 函数来生成随机数。我们了解下它构造函数和基本的使用方法:
numpy.random.randint(low, high=None, size=None, dtype=’l’)
返回随机整数,范围区间为 [low,high],包含 low,不包含 high
参数:low 为最小值,high 为最大值,size 为数组维度大小,dtype 为数据类型,默认的数据类型是 np.int
high 没有填写时,默认生成随机数的范围是 [0,low]
print("np.random.randint:\n {}".format(np.random.randint(1,size=5)))# 返回 [0,1) 之间的整数,所以只有 0
"""
np.random.randint:
[0 0 0 0 0]
"""
print("np.random.randint:\n {}".format(np.random.randint(1,5)))# 返回 1 个 [1,5) 时间的随机整数
"""
np.random.randint:
2
"""
print("np.random.randint:\n {}".format(np.random.randint(-5,5,size=(2,2))))
"""
np.random.randint:
[[-5 -3]
[ 2 -3]]
"""注:需要说明的是 random 模块产生的随机数是伪随机数,依赖于特殊算法和指定不确定因素 (种子 seed) 来实现的,不过这并不妨碍我们进行实验。
3. 预知随机漫步的规律
有研究称股票每天的价格变动就像醉汉行走一样不可预知,接下来我们用 Python 来重现醉汉的随机漫步。
我们假设一名喝醉了酒的醉汉,从一个路灯下开始漫无目的地行走,每一步即可能前进也可能后退也可能拐弯。那么经过一定时间之后,这名醉汉的位置在哪里呢?为了便于理解,我们将醉汉的移动简化为一维的移动,规定他只能在一条直线上随机前进或者后退。
我们使用上文提到的 numpy.random.randint() 函数来产生 2000 个随机数,作为随机游走的路线,实现代码如下所示:
draws = np.random.randint(0, 2, size=2000)
print(f'random walk direction is {draws}')
#random walk direction is [1 0 1 ... 0 1 0]然后我们使用 matplotlib.pyplot.plot() 函数绘制出醉汉从 0 轴开始随机游走 2000 步的模拟轨迹图形,如图 1-1 所示:
从中可知在 2000 次漫步中,终点的距离为 32,第 1595 步前进最远的距离为 64,第 142 步后退最远的距离为 -25。我们把随机漫步轨迹的计算封装为函数 random_walk(),此处分享实现的代码,如下所示:
def draw_random_walk():
walk_steps = 2000
walk_path = random_walk(walk_steps)
# 统计漫步过程中,终点、前进和后退最大的距离
start_y = 0
start_x = 0
end_y = walk_path[-1]
end_x = walk_steps-1
max_y = walk_path.max()
max_x = walk_path.argmax()
min_y = walk_path.min()
min_x = walk_path.argmin()
x = np.linspace(0, 2000, num=2000)
# 绘制出漫步的足迹
plt.plot(x, walk_path, color='b', linewidth=1, label='walk step')
# 添加标注
# 起点坐标
plt.annotate(
'start:({},{})'.format(start_x, start_y),
xy = (start_x,start_y),
xycoords='data',
xytext=(+50, +20),
textcoords='offset points',
fontsize=8,
bbox=dict(boxstyle='round,pad=0.5',fc ='yellow', alpha = 0.5),
arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2")
)
# 终点坐标
plt.annotate(
'end:({},{})'.format(end_x, end_y),
xy = (end_x,end_y),
xycoords='data',
xytext=(-50, +20),
textcoords='offset points',
fontsize=8,
bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2")
)
# 最大距离坐标
plt.annotate(
'max:({},{})'.format(max_x,max_y),
xy = (max_x,max_y),
xycoords = 'data',
xytext = (-20, +20),
textcoords='offset points',
fontsize = 8,
bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2")
)
# 最小距离坐标
plt.annotate(
'min:({},{})'.format(min_x,min_y),
xy = (min_x,min_y),
xycoords = 'data',
xytext = (-20, +20),
textcoords='offset points',
fontsize = 8,
bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2")
)
plt.legend(loc='best')
plt.xlabel('游走步数')
plt.ylabel('分布轨迹')
plt.title(u"模拟随机漫步")
plt.show()由于醉汉的每一步都是完全随机的,因此他最终准确的位置无法被预测出,就像每天的股票价格变动一样是不可预知的。但是,量化交易会从统计学的角度去分析问题,我们用 1000 次随机漫步来模拟醉汉从 0 轴开始 1000 次随机游走 2000 步的模拟轨迹图形,如图 1-2 所示:
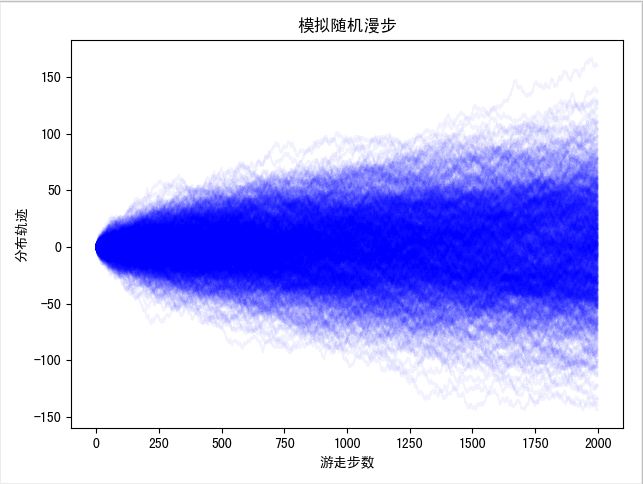
从统计学的角度来看,这名醉汉最终的位置的概率分布却是可以计算出来的。图中我们直观地观察出随机游走的发展情况,每一条淡淡的蓝线就是一次模拟,横轴为行走的步数,纵轴表示离开起始点的位置。蓝色越深,就表示醉汉在对应行走了对应的步数之后,出现在此位置的概率越大,可见随着醉汉可能出现的位置的范围不断变大,但是距离起始点越远的位置概率越小。
于是我们联想到正态分布。正态分布是连续随机变量概率分布的一种,也称“常态分布”、“高斯分布”(Gaussian distribution),最早的正态分布概念其实是由德国的数学家和天文学家阿伯拉罕·德莫弗尔 (Abraham de Moivre) 于 1733 年首次提出的,但由于德国数学家 Gauss 率先将其应用于天文学家研究,故正态分布又叫高斯分布。
正态分布描述的是某件事出现不同结果的概率分布情况,它的概率密度曲线的形状是两头低,中间高,左右对称呈钟型,与我们模拟的随机漫步图很相似。接下来我们继续验证,使用 matplotlib.pyplot 库中的 hist() 函数将随机漫步的位置绘制为直方图。如图 1-3 所示:
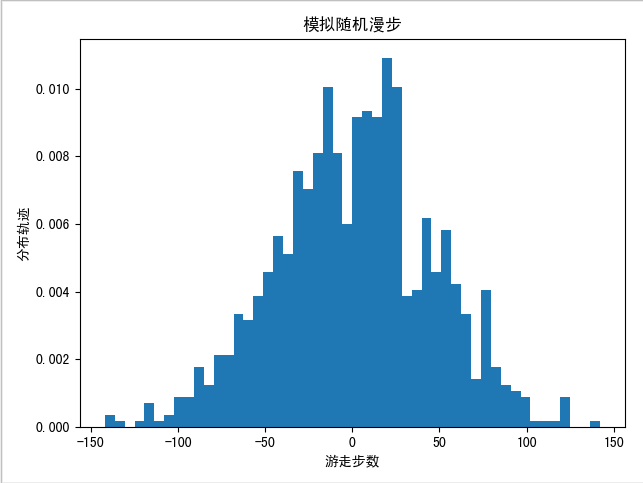
从图中的显示可知醉汉的行走轨迹在一定意义上是符合正态分布的。可见正态分布现象在现实中意义重大,在自然界、人类社会、心理学等领域的大量现象中都服从或者近似服从正态分布,比如人们能力的高低,身高、体重等身体的状态,学生成绩的好坏,人们的社会态度、行为表现等等。不禁感慨道:数学的奇妙之处就在于,我们可以把不可预知性变为可预知。
4. 总结
金融证券市场一直充满了随机性,但是量化交易的精髓就是用数学公式来精确计算真实的概率分布,以应对不确定性。量化交易的鼻祖级大神爱德华·索普就是利用这种随机游走模型的思想,推算出认股权证在合约兑现的那一天相对应的股票的价格的概率分布,从而计算出当前认股权证的价格是过高还是过低,然后再利用凯利公式,进行买卖。笔者以模拟随机漫步为切入点将文中用 Python 分析金融数据的方法分享给大家,希望能够对大家有所启发。