第23章《最小生成树》: Kruskal和Prim算法，python实现

最小生成树

假设一个连通无向图$G=(V,E)$，其中每条边$(u,v)\in E$，我们为其赋予权重$w(u,v)$，我们希望找到一个无环子集$T\subseteq E$，既能够将所有的节点连接起来，又具有最小的权重。即$w(T)={\sum }_{(u,v)\in T}w(u.v)$的值最小。由于$T$是无环的，并且连通所有的节点，因此，$T$必然是一棵树。我们称这样的树为生成树，我们称求取该生成树的问题为最小生成树问题。如下图描述的是一个连通图及其最小生成树的例子：

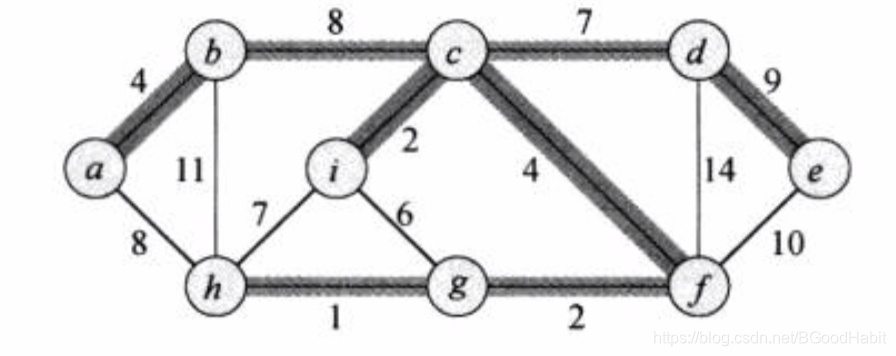
在图中，属于最小生成树的边加上了阴影，图中所示的生成树的总权重为37，不过，该最小生成树并不是唯一的，删除边$(b,c)$，然后加入边$(a,h)$，将形成另一颗权重也是37的最小生成树。
解决zui最小生成树问题的两种算法：Kruskal算法和Prim算法，两种最小生成树算法都是贪心算法。

Kruskal算法和Prim算法

最小生成树问题的两个经典算法，在Kruskal算法中，集合$A$是一个森林，其节点就是给定图的节点，每次加入到集合$A$中的安全边永远是权重最小的连接两个不同分量的边，在Prim算法里，集合$A$则是一棵树，每次加入到$A$中的安全边永远是连接$A$和$A$之外某个节点的边中权重最小的边。

Kruskal算法

Kruskal算法找到安全边的办法是，在所有连接森林中两颗不同树的边里面，找到权重最小的边$(u,v)$，Kruskal算法属于贪心算法，因为它每次都选择一条权重最小的边加入森林。如下图是Kruskal算法的工作过程：

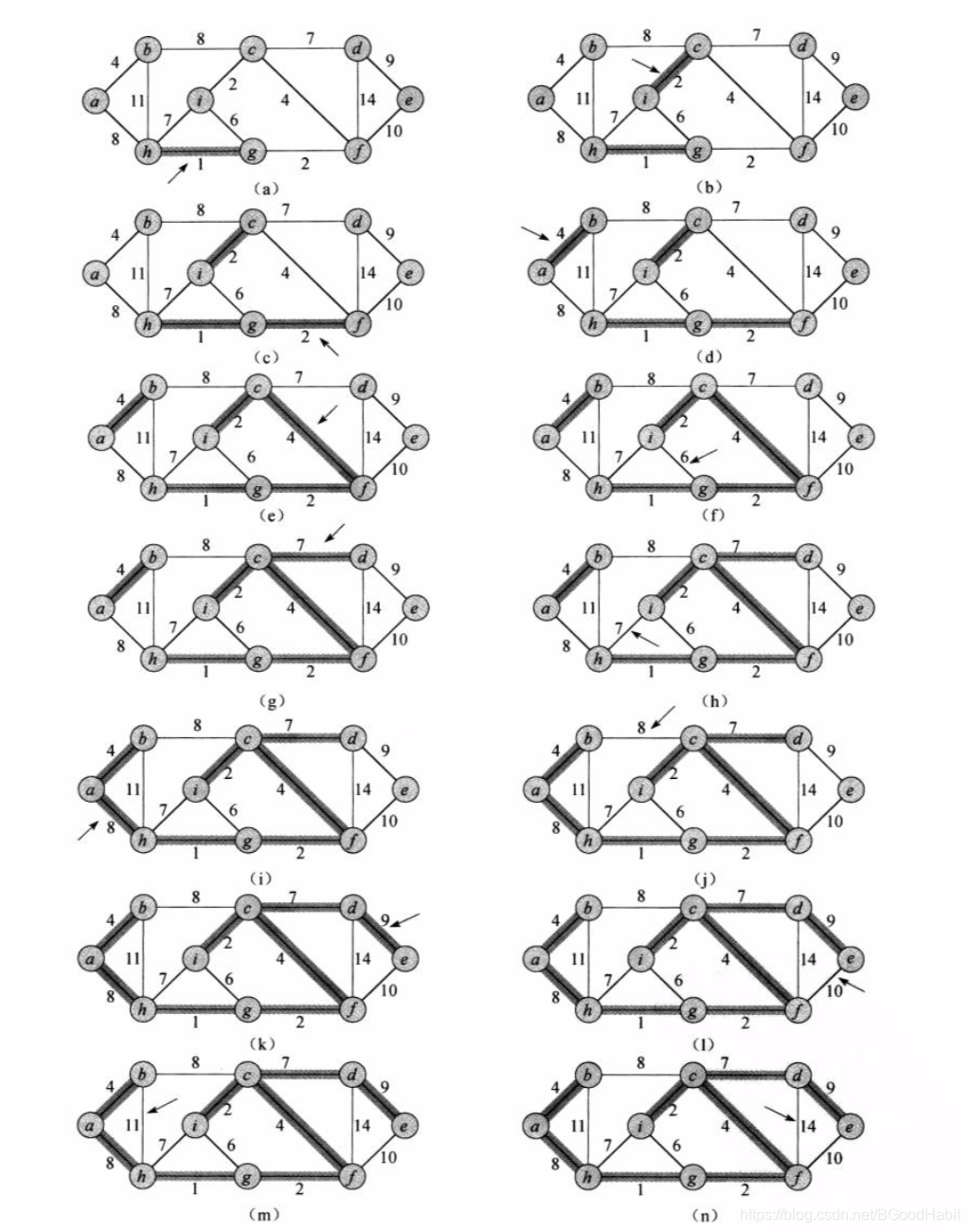
加了阴影的边属于不断增长的森林$A$，该算法按照边的权重大小依次进行考虑，箭头指向的边是算法每一步所考察的边。如果该边将两颗不同的树连接起来，它就被加入到森林里，从而完成对两颗树的合并。

实现思路

输入：图
输出：最小树
最小树满足条件：

• 包含了所有的节点
• 在图构成的所有树中，是总分值最小的树

实现步骤

1. 对所有的边根据权重进行从小到大排序
2. 每次选择最小的边加入到树中，如果新增加的边导致树中有环，则丢弃该条边
3. 重复上面2增加边的操作，直到树包含了所有的节点

python实现代码如下：

# -*-coding:utf8 -*-
import sys


class Graph:
	def __init__(self, vertices):
		self.V = vertices
		self.graph = []
	
	def add_edge(self, u, v, w):
		self.graph.append([u,v,w])

	# 找到节点所在的树的根节点
	def find(self, parent, i):
		if parent[i] == i:
			return i
		return self.find(parent, parent[i])

	# 合并新的节点到一棵树中来
	def apply_union(self, parent, rank, x, y):
		xroot = self.find(parent, x)
		yroot = self.find(parent, y)
		if rank[xroot] < rank[yroot]:
			parent[xroot] = yroot
		elif rank[xroot] > rank[yroot]:
			parent[yroot] = xroot
		else:
			parent[yroot] = xroot
			rank[xroot] +=1

	def kruskal(self):
		result = []
		i, e = 0, 0
		#排序，边按照权重从小到大排序
		self.graph = sorted(self.graph, key=lambda item: item[2])
		parent = []
		rank = []
		#初始，每个节点构成一棵树，根节点就是自己
		for node in range(self.V):
			parent.append(node)
			rank.append(0)
		# 做V-1个节点选择
		while e < self.V - 1:
			u, v, w = self.graph[i]
			i = i+1
			x = self.find(parent, u)
			y = self.find(parent, v)
			# 选择的边的两个节点不在同一棵树,则合并
			if x != y:
				e = e + 1
				result.append([u, v, w])
				self.apply_union(parent, rank, x, y)
		#打印每一次选择的边
		for u, v , weight in result:
			print("%d - %d: %d" % (u, v, weight))


if __name__=='__main__':
	g = Graph(6)
	for x,y,w in [(0,1,4),(0,2,4),(1,2,2),(1,0,4),(2,0,4),(2,1,2),(2,3,3),(2,5,2),(2,4,4),(3,2,3),(3,4,3),(4,2,4),(4,3,3),(5,2,2),(5,4,3)]:
		g.add_edge(x,y,w)
	g.kruskal()

Kruskal算法的时间复杂度为$O(ElgE)$

Prim算法

Prim算法所具有的一个性质是集合$A$中的边总是构成一棵树，这棵树从一个任意的根节点开始，一直长大到覆盖$V$中的所有节点时为止。本策略也属于贪心策略，因为每一步加入的边都必须是使树的总权重增加量最小的边。
如下图执行Prim算法的过程，初始节点为$a$，加阴影的边和黑色的节点都属于树$A$。

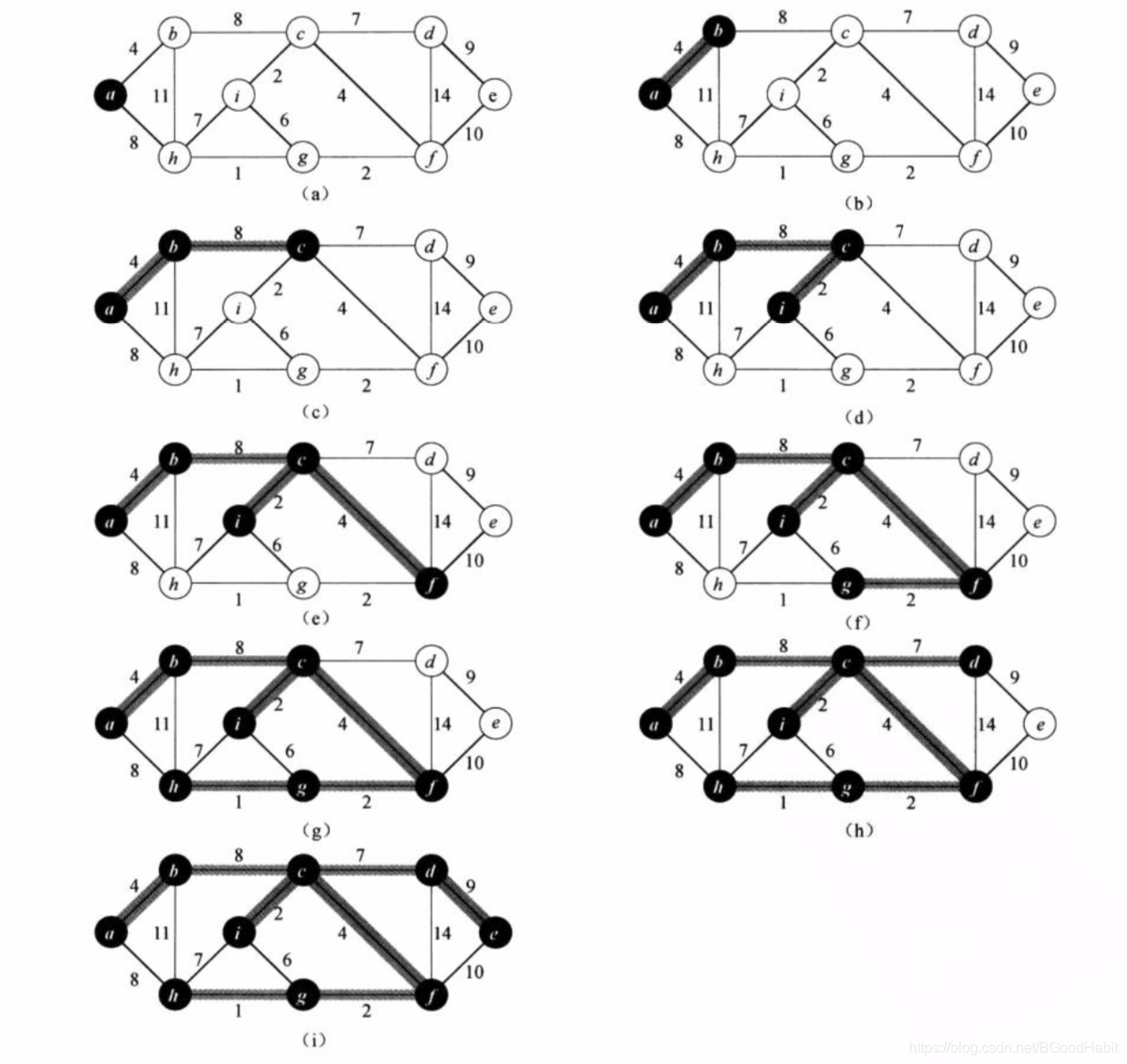
实现步骤

1. 随机选择一个节点初始化最小树
2. 对所有的连接该树和新节点的边，选择最小权重的边
3. 重复上述2，直到包含所有的节点

python实现如下：

# -*-coding:utf8 -*-
import sys
INF = 9999999


class Graph: 
	def __init__(self, V, G):
		self.V = V
		self.G = G

	def prim(self):
		selected = [0] * self.V
		no_edge = 0
		selected[0] = True
		print("Edge : Weight")
		#需要选择V-1个
		while (no_edge < self.V - 1):
			minimum = INF
			x = 0
			y = 0
			# 遍历V个节点 
			for i in range(V):
				#该节点选择了的
				if selected[i]:
					for j in range(self.V):
						#选择的邻接节点没有选择的，且有边的
						if ((not selected[j]) and self.G[i][j]):  
							if minimum > self.G[i][j]:
								minimum = self.G[i][j]
								x = i
								y = j
			print(str(x) + "-" + str(y) + ":" + str(self.G[x][y]))
			selected[y] = True
			no_edge += 1

if __name__=='__main__':
	V = 5
	G = [[0, 9, 75, 0, 0],
     [9, 0, 95, 19, 42],
     [75, 95, 0, 51, 66],
     [0, 19, 51, 0, 31],
     [0, 42, 66, 31, 0]]	
	graph = Graph(V,G)
	graph.prim()	

Prim的算法复杂度为$O(ElogV)$