8.2 B-树

参考博客：https://blog.csdn.net/weixin_41698717/article/details/107663202
参考博客：https://blog.csdn.net/amoscykl/article/details/81592543
参考博客：https://blog.csdn.net/qq_34645958/article/details/80863755
参考博客：https://blog.csdn.net/i6223671/article/details/86761107

本章问题

1.在进行测试时发现结果与正确运行的结果不相符

推测自己写的Vector出了问题，发现原本的Vector查找算法写错，
调用接口返回的是不大于该数的最大秩，而Fib查找，没找到的话会返回-1，所以必须一直用二分查找
Vector中的代码改为

//二分查找算法: 在有序区间[lo,hi)内查找元素e，0<=lo<=hi<=_size
template <typename T> static Rank binSearch(T *A,T const&e,Rank lo,Rank hi)
{
    
    
    while(lo<hi){
    
    //每步迭代仅需做一次比较判断,有两个分支: 成功查找不能提前终止
        Rank mi=(lo+hi)>>1;//以中点为轴点
        (e<A[mi])?hi=mi:lo=mi+1;//经比较后确定深入[lo,hi)或(mi,hi)
    }//成功查到不能提前终止
    return --lo;//循环结束时，为大于e的元素的最小秩，故lo-1即不大于e的元素的最大秩
}//有多个命中元素时，总保证返回秩元素最大者;查找失败时能够返回失败的位置

Rank Vector<T>::search(T const&e,Rank lo,Rank hi)const//assert: 0<=lo<hi<=_size
{
    
    
    return */(rand()%2)*/ 1?//按50%的概率随机使用二分查找和Fibonacci查找
    binSearch(_elem,e,lo,hi):fibSearch(_elem,e,lo,hi);
}
    Rank search(T const&e)//有序向量整体查找
    {
    
    return(0>=_size)?-1:search(e,0,_size);}

2. 查找算法时使用了Vector的二分查找，说明关键码有序，那么关键码是如何保持有序的

插入元素时直接插入对应的位置，保持关键码向量始终有序

3. 什么是B-树(多路搜索树)

多路搜索树

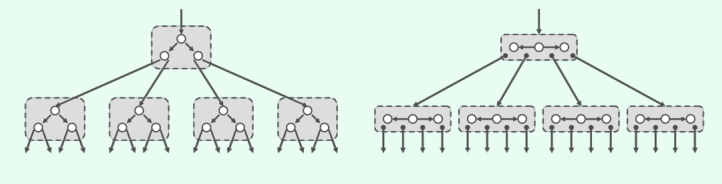
具体地如图所示,比如可以两层为间隔,将各节点与其左、右孩子合并为“大节点”，每个“大节点”拥有四个分支,故称作四路搜索树。一般地,以k层为间隔如此重组,可将二叉搜索树转化为等价的2^k路搜索树,统称多路搜索树(multi-way search tree)。

多路平衡搜索树
所谓m阶B-树 (B-tree),即m路平衡搜索树(m >= 2),其宏观结构如图
外部节点以深色示意，深度完全一致，且都同处于最底层

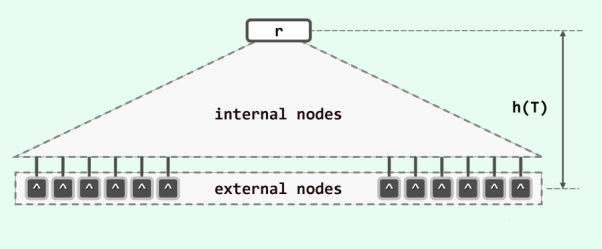
4阶B树：即2-3-4树

(a ): 四阶B-树
(b ): B-树的紧凑表示
(c ): B-树的最紧凑表示

4.B-树的定义是什么

注意：叶子结点也叫终端结点，是出度为 0 的结点。

m阶的B树，或为空树，或为满足以下性质的树：
1.树中每个结点至多有m棵子树；
2.若根结点不是叶子结点，则至少有2棵子树；
3.除根结点和叶子结点外，其它每个结点至少有[m/2]个孩子；
4.所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息,通常称为失败节点
(失败节点并不存在，指向这些节点的指针为空。引入失败节点是为了便于分析B-树的查找性能)
5.所有非叶子节点最多有m-1个关键字

5.在查找中运用的B-树的性质是什么

树中每个节点中的关键字都是有序的，且关键字K_i"左子树"中的关键字均小于K_i，而其"右子树"中的关键字均大于K_i

4.B-树怎样查找关键码的

算法查找时：
1.若key==K_i,(1 $\leq$ i $\leq$ j),则查找成功
2.当然如果key<K₀,则查找失败的秩返回的值为-1，顺着孩子指针child[0],继续向下查找
3.若K_i<key<K_i+1, 此时r=i-1, 则顺着孩子指针v->child[r+1]继续向下查找,这里r是不大于e的最大的关键码的秩
4.若key>K_j,则顺着孩子指针child[j+1], 向下继续查找(这里的 j 主要是指关键码的最后一个元素)。
注意：孩子向量其长度总比key向量多一

一般地如图所示,可以将大数据集组织为B-树并存放于外存。对于活跃的B-树,其根节点会常驻于内存;此外,任何时刻通常只有另一节点(称作当前节点)留驻于内存。

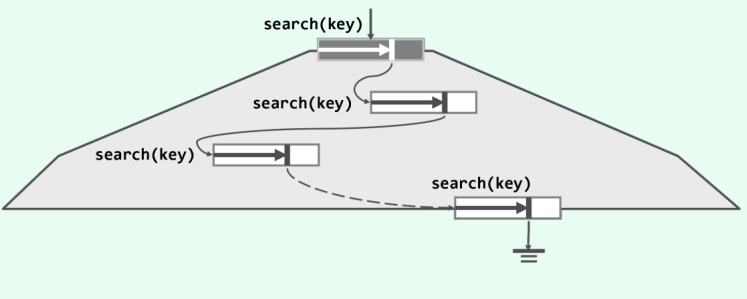
与二叉搜索树的不同之处在于,因此时各节点内通常都包含多个关键码,故有可能需要经过(在内存中的)多次比较,才能确定应该转向下一层的哪个节点并继续查找。

5.B-树怎么插入关键码的

查找算法过程：
1.首先调用search(e )在树中查找关键码，若查找成功，则按照按照"禁止重复关键码"的约定不予插入，操作即完成并返回false
2.否则，代码出口约定, 查找过程必然终止于某一外部节点v,且其父节点由变量_hot指示。当然，此时此时的_hot必然指向某一叶节点也可能是根节点。
3.接下来,在该节点的关键码向量中再次查找，目标关键码e。尽管这次查找注定失败,却可以确定e在其关键码向量的正确插入位置r。最后,只需将e插至这一位置。
4.若该节点内关键码的总数依然合法(即不超过m-1个)，则操作完成
5.否则，称该节点发生了一次上溢，此时需要通过适当的处理，使得该节点和整树重新满足B-树的条件

6.上溢算法怎样通过分裂解决上溢的

算法
一般地,刚发生上溢的节点,应恰好含有m个关键码。若取s = [m/2] ,则它们依次为:
{ k ₀, …, k _s-1 ;k _s ;k _s+1 , …, k _m-1 }
可见,以k s 为界,可将该节点分前、后两个子节点,且二者大致等长。于是,可令关键码k s上升一层,归入其父节点(若存在)中的适当位置,并分别以这两个子节点作为其左、右孩子。这一过程,称作节点的分裂(split)。

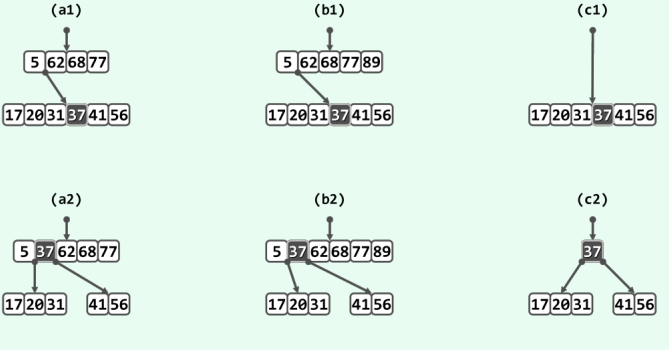
如图(a1)所示,设原上溢节点的父节点存在,且足以接纳一个关键码。此种情况下,只需将被提升的关键码(37)按次序插入父节点中,修复即告完成,修复后的局部如图(a2)所示。
如图(b1)所示,尽管上溢节点的父节点存在,但业已处于饱和状态。此时如图(b2),在强行将被提升的关键码插入父节点之后,尽管上溢节点也可得到修复,却会导致其父节点继而发生上溢这种现象称作上溢的向上传递。好在每经过一次这样的修复,上溢节点的高度都必然上升一层。这意味着上溢的传递不至于没有尽头,最远不至超过树根。
如图(c1)所示,若上溢果真传递至根节点,则可令被提升的关键码(37)自成一个节点,并作为新的树根。

7.B-树怎么删除节点的

删除算法步骤:
1.确认关键码存在，如果不存在直接返回false
2.找到关键码在向量中的秩
3.找到该关键码的后继，与待删除元素交换，并删除关键码(类似BST中的替换删除法)
4.如有必要进行，合并操作

8.B-树怎么进行合并操作的

删除非终端节点：首先找到要删除的关键码所在结点，**用指针Ai（右指针）所指子树中最小关键码Y代替Ki，**然后在相应终端结点中删去Y，这样就转为删除终端结点中的关键码的问题了。

删除终端节点:
（1）被删关键码所在结点中的关键码个数>=[m/2],说明删去该关键字后该结点仍满足B-树的定义。
这种情况最为简单，只需从该结点中直接删去关键字即可。

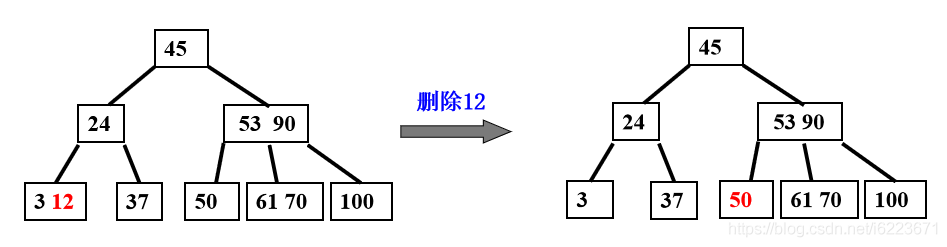
（2）被删关键码所在结点中关键码个数n=[m/2]-1，说明删去该关键字后该结点将不满足B-树的定义，需要调整。
调整过程分为两种：

①如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右（左）兄弟结点中的关键字数目大于[m/2]-1。
则可将右（左）兄弟结点中最小（大）关键字上移至双亲结点。而将双亲结点中小（大）于该上移关键字的最大（小）关键字下移至被删关键字所在结点中。
父母中紧靠被删关键字的下来，兄弟中紧靠被删关键字的关键字上取

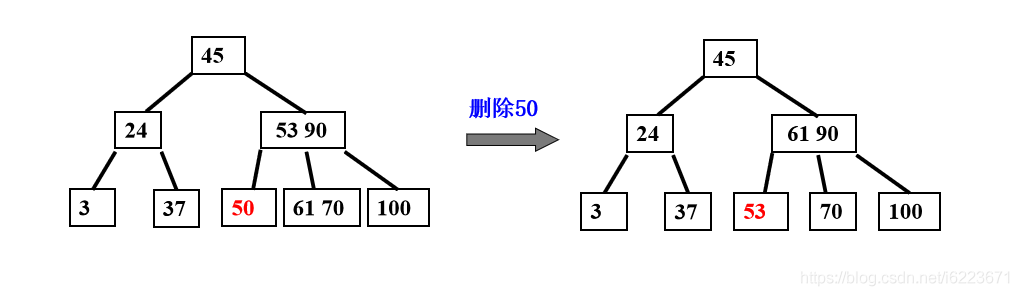
②被删关键码所在结点和其相邻的左右兄弟节点中的关键码个数均等于[m/2]-1，左右兄弟都不够借。
需把要删除关键字的结点与其左（或右）兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后，该结点中剩余的关键字加指针，加上双亲结点中的关键字Ki一起，合并到Ai（即双亲结点指向该删除关键字结点的左（右）兄弟结点的指针）所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于[m/2]-1，则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。
父母节点中与被删的关键字紧靠的关键字下来，然后去和兄弟节点合并

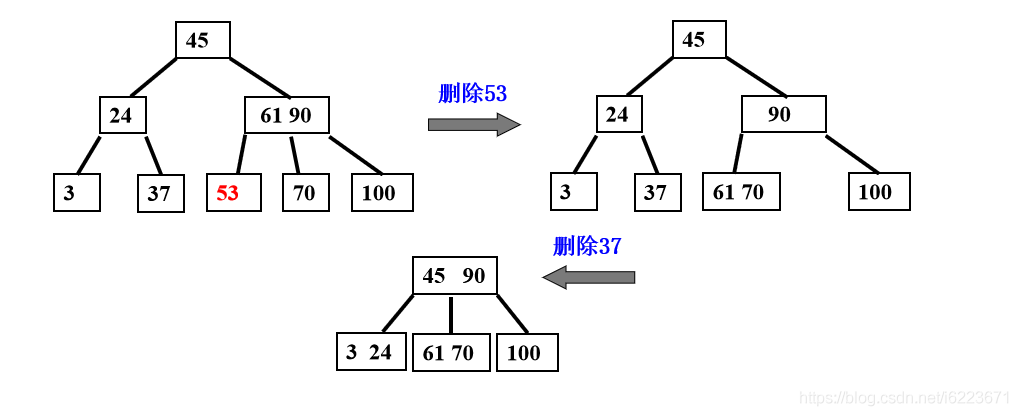
注意：发现母亲节点也不够删除的时候，将母亲节点这一层看做叶子，连带着其孩子看着整体一起移动

8.2.1 B-树ADT接口

操作	功能
solveOverflow()	因插入而上溢的分裂处理
solveUnderflow()	因删除而下溢之后的合并处理
search()	查找
insert()	插入
remove()	删除

8.2.2 BTNode类

#include "vector.h"
#define BTNodePosi(T) BTNode<T>*
template <typename T> struct BTNode {
    
    
//成员
    BTNodePosi(T) parent;//父亲节点
    Vector<T> key;//关键码向量
    Vector<BTNodePosi(T)> child;//孩子向量
//构造函数
    BTNode() {
    
     parent = nullptr; child.insert ( 0, nullptr );}
    BTNode( T e, BTNodePosi(T) lc = nullptr, BTNodePosi(T) rc = nullptr){
    
    
        parent = nullptr;
        key.insert( 0, e );//一个关键码
        child.insert( 0, lc );child.insert( 1, rc );//两个孩子
        if ( lc ) lc->parent = this; if( rc ) rc->parent = this;
    }
};

8.2.3 BTree类

#include "btnode.h"
#include "release.h"

template <typename T> class BTree{
    
    
protected:
    int _size;//关键码总数
    int _order;//B树的阶数
    BTNodePosi(T) _root;
    BTNodePosi(T) _hot;//BTree::search()最后访问的非空的节点位置
    void solveOverflow( BTNodePosi(T) );//因插入而上溢后的分裂处理
    void solveUnderflow( BTNodePosi(T) );//因删除而下溢后的合并处理
public:
    BTree ( int order = 3 ) : _order ( order ), _size( 0 ) {
    
     _root = new BTNode<T>(); }
    ~BTree() {
    
     if( _root ) dtl::release ( _root );}
    int const order() {
    
     return _order; }
    int const size() {
    
     return _size; }
    BTNodePosi(T) & root() {
    
     return _root; }
    bool empty() const{
    
     return !_root; }
    BTNodePosi(T) search( const T& e );
    bool insert( const T& e );
    bool remove( const T& e );
};//BTree

8.2.4 查找

//查找
template <typename T> BTNodePosi(T) BTree<T>::search ( const T& e ){
    
    
    BTNodePosi(T) v = _root; _hot = nullptr;
    while( v ){
    
    
        Rank r = v->key.search( e );
        if( ( 0 <= r ) && ( e == v->key[r] )) return v;
        _hot = v; v = v->child[ r + 1 ];
    }
    return nullptr;
}

8.2 5 solveOverflow()上溢

//上溢处理
template <typename T> void BTree<T>::solveOverflow( BTNodePosi(T) v ){
    
    
    if ( _order >= v->child.size() ) return;//递归基
    Rank s = _order / 2;
    BTNodePosi(T) u = new BTNode<T>();
    for( Rank j = 0; j < _order - s - 1; ++j ){
    
    
        u->child.insert( j, v->child.remove( s + 1 ));
        u->key.insert( j, v->key.remove( s + 1 ));
    }
    u->child[ _order - s - 1 ] = v->child.remove( s + 1 );
    if ( u->child[0] )
        for ( Rank j = 0; j < _order - s; ++j )
            u->child[j]->parent = u;
    BTNodePosi(T) p = v->parent;
    if( !p ) {
    
     _root = p = new BTNode<T>(); p->child[0] = v; v->parent = p; }
    Rank r = 1 + p->key.search( v->key[0] );
    p->key.insert( r, v->key.remove( s ));
    p->child.insert( r + 1, u ); u->parent = p;
    solveOverflow( p );
}

8.2.6 插入

//插入
template <typename T> bool BTree<T>::insert( const T& e ){
    
    
    BTNodePosi(T) v = search( e ); if( v ) return false;
    Rank r = _hot->key.search( e );//获取插入位置
    _hot->key.insert( r + 1, e );
    _hot->child.insert( r + 2, nullptr );
    _size ++;
    solveOverflow( _hot );
    return true;
}

8.2.6 solveUnderflow()下溢

//节点下溢算法
template <typename T> //关键码删除后若节点下溢，则做节点旋转或合并处理
void BTree<T>::solveUnderflow ( BTNodePosi(T) v ) {
    
    
   if ( ( _order + 1 ) / 2 <= v->child.size() ) return; //递归基：当前节点并未下溢
   BTNodePosi(T) p = v->parent;
   if ( !p ) {
    
     //递归基：已到根节点，没有孩子的下限
      if ( !v->key.size() && v->child[0] ) {
    
    
         //但倘若作为树根的v已不含关键码，却有（唯一的）非空孩子，则
         _root = v->child[0]; _root->parent = NULL; //这个节点可被跳过
         v->child[0] = NULL; dtl::release ( v ); //并因不再有用而被销毁
      } //整树高度降低一层
      return;
   }
   Rank r = 0; while ( p->child[r] != v ) r++;
   //确定v是p的第r个孩子——此时v可能不含关键码，故不能通过关键码查找
   //另外，在实现了孩子指针的判等器之后，也可直接调用Vector::find()定位

// 情况1：向左兄弟借关键码
   if ( 0 < r ) {
    
     //若v不是p的第一个孩子，则
      BTNodePosi(T) ls = p->child[r - 1]; //左兄弟必存在
      if ( ( _order + 1 ) / 2 < ls->child.size() ) {
    
     //若该兄弟足够“胖”，则
         v->key.insert ( 0, p->key[r - 1] ); //p借出一个关键码给v（作为最小关键码）
         p->key[r - 1] = ls->key.remove ( ls->key.size() - 1 ); //ls的最大关键码转入p
         v->child.insert ( 0, ls->child.remove ( ls->child.size() - 1 ) );
         //同时ls的最右侧孩子过继给v
         if ( v->child[0] ) v->child[0]->parent = v; //作为v的最左侧孩子
         return; //至此，通过右旋已完成当前层（以及所有层）的下溢处理
      }
   } //至此，左兄弟要么为空，要么太“瘦”
// 情况2：向右兄弟借关键码
   if ( p->child.size() - 1 > r ) {
    
     //若v不是p的最后一个孩子，则
      BTNodePosi(T) rs = p->child[r + 1]; //右兄弟必存在
      if ( ( _order + 1 ) / 2 < rs->child.size() ) {
    
     //若该兄弟足够“胖”，则
         v->key.insert ( v->key.size(), p->key[r] ); //p借出一个关键码给v（作为最大关键码）
         p->key[r] = rs->key.remove ( 0 ); //ls的最小关键码转入p
         v->child.insert ( v->child.size(), rs->child.remove ( 0 ) );
         //同时rs的最左侧孩子过继给v
         if ( v->child[v->child.size() - 1] ) //作为v的最右侧孩子
            v->child[v->child.size() - 1]->parent = v;
         return; //至此，通过左旋已完成当前层（以及所有层）的下溢处理
      }
   } //至此，右兄弟要么为空，要么太“瘦”
// 情况3：左、右兄弟要么为空（但不可能同时），要么都太“瘦”——合并
   if ( 0 < r ) {
    
     //与左兄弟合并
      BTNodePosi(T) ls = p->child[r - 1]; //左兄弟必存在
      ls->key.insert ( ls->key.size(), p->key.remove ( r - 1 ) ); p->child.remove ( r );
      //p的第r - 1个关键码转入ls，v不再是p的第r个孩子
      ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
      if ( ls->child[ls->child.size() - 1] ) //v的最左侧孩子过继给ls做最右侧孩子
         ls->child[ls->child.size() - 1]->parent = ls;
      while ( !v->key.empty() ) {
    
     //v剩余的关键码和孩子，依次转入ls
         ls->key.insert ( ls->key.size(), v->key.remove ( 0 ) );
         ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
         if ( ls->child[ls->child.size() - 1] ) ls->child[ls->child.size() - 1]->parent = ls;
      }
      dtl::release ( v ); //释放v
   } else {
    
     //与右兄弟合并
      BTNodePosi(T) rs = p->child[r + 1]; //右兄度必存在
      rs->key.insert ( 0, p->key.remove ( r ) ); p->child.remove ( r );
      //p的第r个关键码转入rs，v不再是p的第r个孩子
      rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
      if ( rs->child[0] ) rs->child[0]->parent = rs; //v的最左侧孩子过继给ls做最右侧孩子
      while ( !v->key.empty() ) {
    
     //v剩余的关键码和孩子，依次转入rs
         rs->key.insert ( 0, v->key.remove ( v->key.size() - 1 ) );
         rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
         if ( rs->child[0] ) rs->child[0]->parent = rs;
      }
      dtl::release ( v ); //释放v
   }
   solveUnderflow ( p ); //上升一层，如有必要则继续分裂——至多递归O(logn)层
   return;
}

8.2.7 删除

//删除
template <typename T> bool BTree<T>::remove ( const T& e ) {
    
     //从BTree树中删除关键码e
   BTNodePosi(T) v = search ( e ); if ( !v ) return false; //确认目标关键码存在
   Rank r = v->key.search ( e ); //确定目标关键码在节点v中的秩（由上，肯定合法）
   if ( v->child[0] ) {
    
     //若v非叶子，则e的后继必属于某叶节点
      BTNodePosi(T) u = v->child[r+1]; //在右子树中一直向左，即可
      while ( u->child[0] ) u = u->child[0]; //找出e的后继
      v->key[r] = u->key[0]; v = u; r = 0; //并与之交换位置
   } //至此，v必然位于最底层，且其中第r个关键码就是待删除者
   v->key.remove ( r ); v->child.remove ( r + 1 ); _size--; //删除e，以及其下两个外部节点之一
   solveUnderflow ( v ); //如有必要，需做旋转或合并
   return true;
}

8.2.8 BTree.h

#include "btnode.h"
#include "release.h"

template <typename T> class BTree{
    
    
protected:
    int _size;//关键码总数
    int _order;//B树的阶数
    BTNodePosi(T) _root;
    BTNodePosi(T) _hot;//BTree::search()最后访问的非空的节点位置
    void solveOverflow( BTNodePosi(T) );//因插入而上溢后的分裂处理
    void solveUnderflow( BTNodePosi(T) );//因删除而下溢后的合并处理
public:
    BTree ( int order = 3 ) : _order ( order ), _size( 0 ) {
    
     _root = new BTNode<T>(); }
    ~BTree() {
    
     if( _root ) dtl::release ( _root );}
    int const order() {
    
     return _order; }
    int const size() {
    
     return _size; }
    BTNodePosi(T) & root() {
    
     return _root; }
    bool empty() const{
    
     return !_root; }
    BTNodePosi(T) search( const T& e );
    bool insert( const T& e );
    bool remove( const T& e );
};//BTree

//查找
template <typename T> BTNodePosi(T) BTree<T>::search ( const T& e ){
    
    
    BTNodePosi(T) v = _root; _hot = nullptr;
    while( v ){
    
    
        Rank r = v->key.search( e );
        if( ( 0 <= r ) && ( e == v->key[r] )) return v;
        _hot = v; v = v->child[ r + 1 ];
    }
    return nullptr;
}
//插入
template <typename T> bool BTree<T>::insert( const T& e ){
    
    
    BTNodePosi(T) v = search( e ); if( v ) return false;
    Rank r = _hot->key.search( e );
    _hot->key.insert( r + 1, e );
    _hot->child.insert( r + 2, nullptr );
    _size ++;
    solveOverflow( _hot );
    return true;
}

//上溢处理
template <typename T> void BTree<T>::solveOverflow( BTNodePosi(T) v ){
    
    
    if ( _order >= v->child.size() ) return;//递归基
    Rank s = _order / 2;
    BTNodePosi(T) u = new BTNode<T>();
    for( Rank j = 0; j < _order - s - 1; ++j ){
    
    
        u->child.insert( j, v->child.remove( s + 1 ));
        u->key.insert( j, v->key.remove( s + 1 ));
    }
    u->child[ _order - s - 1 ] = v->child.remove( s + 1 );
    if ( u->child[0] )
        for ( Rank j = 0; j < _order - s; ++j )
            u->child[j]->parent = u;
    BTNodePosi(T) p = v->parent;
    if( !p ) {
    
     _root = p = new BTNode<T>(); p->child[0] = v; v->parent = p; }
    Rank r = 1 + p->key.search( v->key[0] );
    p->key.insert( r, v->key.remove( s ));
    p->child.insert( r + 1, u ); u->parent = p;
    solveOverflow( p );
}

//删除
template <typename T> bool BTree<T>::remove ( const T& e ) {
    
     //从BTree树中删除关键码e
   BTNodePosi(T) v = search ( e ); if ( !v ) return false; //确认目标关键码存在
   Rank r = v->key.search ( e ); //确定目标关键码在节点v中的秩（由上，肯定合法）
   if ( v->child[0] ) {
    
     //若v非叶子，则e的后继必属于某叶节点
      BTNodePosi(T) u = v->child[r+1]; //在右子树中一直向左，即可
      while ( u->child[0] ) u = u->child[0]; //找出e的后继
      v->key[r] = u->key[0]; v = u; r = 0; //并与之交换位置
   } //至此，v必然位于最底层，且其中第r个关键码就是待删除者
   v->key.remove ( r ); v->child.remove ( r + 1 ); _size--; //删除e，以及其下两个外部节点之一
   solveUnderflow ( v ); //如有必要，需做旋转或合并
   return true;
}

//节点下溢算法
template <typename T> //关键码删除后若节点下溢，则做节点旋转或合并处理
void BTree<T>::solveUnderflow ( BTNodePosi(T) v ) {
    
    
   if ( ( _order + 1 ) / 2 <= v->child.size() ) return; //递归基：当前节点并未下溢
   BTNodePosi(T) p = v->parent;
   if ( !p ) {
    
     //递归基：已到根节点，没有孩子的下限
      if ( !v->key.size() && v->child[0] ) {
    
    
         //但倘若作为树根的v已不含关键码，却有（唯一的）非空孩子，则
         _root = v->child[0]; _root->parent = NULL; //这个节点可被跳过
         v->child[0] = NULL; dtl::release ( v ); //并因不再有用而被销毁
      } //整树高度降低一层
      return;
   }
   Rank r = 0; while ( p->child[r] != v ) r++;
   //确定v是p的第r个孩子——此时v可能不含关键码，故不能通过关键码查找
   //另外，在实现了孩子指针的判等器之后，也可直接调用Vector::find()定位

// 情况1：向左兄弟借关键码
   if ( 0 < r ) {
    
     //若v不是p的第一个孩子，则
      BTNodePosi(T) ls = p->child[r - 1]; //左兄弟必存在
      if ( ( _order + 1 ) / 2 < ls->child.size() ) {
    
     //若该兄弟足够“胖”，则
         v->key.insert ( 0, p->key[r - 1] ); //p借出一个关键码给v（作为最小关键码）
         p->key[r - 1] = ls->key.remove ( ls->key.size() - 1 ); //ls的最大关键码转入p
         v->child.insert ( 0, ls->child.remove ( ls->child.size() - 1 ) );
         //同时ls的最右侧孩子过继给v
         if ( v->child[0] ) v->child[0]->parent = v; //作为v的最左侧孩子
         return; //至此，通过右旋已完成当前层（以及所有层）的下溢处理
      }
   } //至此，左兄弟要么为空，要么太“瘦”
// 情况2：向右兄弟借关键码
   if ( p->child.size() - 1 > r ) {
    
     //若v不是p的最后一个孩子，则
      BTNodePosi(T) rs = p->child[r + 1]; //右兄弟必存在
      if ( ( _order + 1 ) / 2 < rs->child.size() ) {
    
     //若该兄弟足够“胖”，则
         v->key.insert ( v->key.size(), p->key[r] ); //p借出一个关键码给v（作为最大关键码）
         p->key[r] = rs->key.remove ( 0 ); //ls的最小关键码转入p
         v->child.insert ( v->child.size(), rs->child.remove ( 0 ) );
         //同时rs的最左侧孩子过继给v
         if ( v->child[v->child.size() - 1] ) //作为v的最右侧孩子
            v->child[v->child.size() - 1]->parent = v;
         return; //至此，通过左旋已完成当前层（以及所有层）的下溢处理
      }
   } //至此，右兄弟要么为空，要么太“瘦”
// 情况3：左、右兄弟要么为空（但不可能同时），要么都太“瘦”——合并
   if ( 0 < r ) {
    
     //与左兄弟合并
      BTNodePosi(T) ls = p->child[r - 1]; //左兄弟必存在
      ls->key.insert ( ls->key.size(), p->key.remove ( r - 1 ) ); p->child.remove ( r );
      //p的第r - 1个关键码转入ls，v不再是p的第r个孩子
      ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
      if ( ls->child[ls->child.size() - 1] ) //v的最左侧孩子过继给ls做最右侧孩子
         ls->child[ls->child.size() - 1]->parent = ls;
      while ( !v->key.empty() ) {
    
     //v剩余的关键码和孩子，依次转入ls
         ls->key.insert ( ls->key.size(), v->key.remove ( 0 ) );
         ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
         if ( ls->child[ls->child.size() - 1] ) ls->child[ls->child.size() - 1]->parent = ls;
      }
      dtl::release ( v ); //释放v
   } else {
    
     //与右兄弟合并
      BTNodePosi(T) rs = p->child[r + 1]; //右兄度必存在
      rs->key.insert ( 0, p->key.remove ( r ) ); p->child.remove ( r );
      //p的第r个关键码转入rs，v不再是p的第r个孩子
      rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
      if ( rs->child[0] ) rs->child[0]->parent = rs; //v的最左侧孩子过继给ls做最右侧孩子
      while ( !v->key.empty() ) {
    
     //v剩余的关键码和孩子，依次转入rs
         rs->key.insert ( 0, v->key.remove ( v->key.size() - 1 ) );
         rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
         if ( rs->child[0] ) rs->child[0]->parent = rs;
      }
      dtl::release ( v ); //释放v
   }
   solveUnderflow ( p ); //上升一层，如有必要则继续分裂——至多递归O(logn)层
   return;
}

8.2.9 BTree测试

#include "btree.h"
#include <iostream>

using namespace std;

int main(){
    
    
    BTree<int> bt;
    bt.insert( 1 );
    /*
    *     1
    */
    bt.insert( 2 );
    /*
    *     1 2
    */
    bt.insert( 3 );
    /*
    *       2
    *   1       3
    */
    bt.insert( 4 );
    cout << bt.root() ->child[1]->key[0] << endl;//3
    /*
    *       2
    *   1      3 4
    */

    bt.insert( 5 );
    cout << bt.root() ->child[1]->key[0] << endl;//3
    /*
    *       2 4
    *   1    3    5
    */    
    bt.insert( 6 );
    cout << bt.root() ->child[2]->key[0] << endl;//5
    /*
    *       2 4
    *   1    3    5 6
    */   
    cout << "-----------"<< endl;
    bt.remove( 3 );
    cout << bt.root() ->child[1]->key[0] << endl;//4
    cout << bt.root()->child[2]->key[0] << endl;//6
     /*
    *       2 5
    *   1    4    6
    */   
}