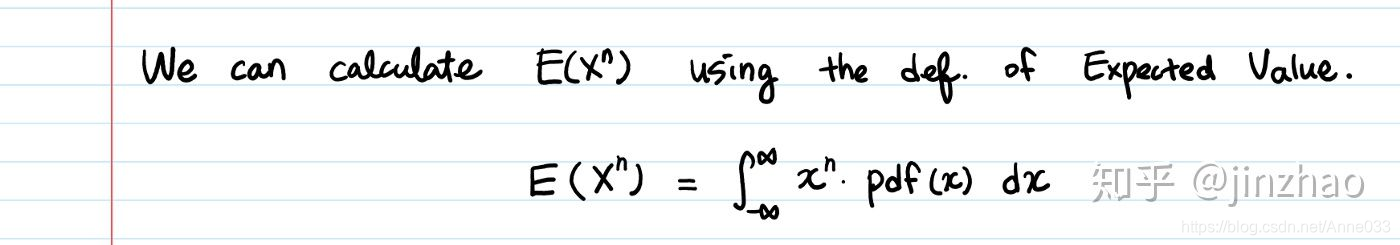1. 简介
在数学中,某个序列的母函数(Generating function,又称生成函数)是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。
母函数可分为很多种,包括普通母函数、指数母函数、L级数、贝尔级数和狄利克雷级数。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。
这里先给出两句话,不懂的可以等看完这篇文章再回过头来看:
1.“把组合问题的加法法则和幂级数的乘幂对应起来”
2.“母函数的思想很简单 — 就是把离散数列和幂级数一 一对应起来,把离散数列间的相互结合关系对应成为幂级数间的运算关系,最后由幂级数形式来确定离散数列的构造. “
我们首先来看下这个多项式乘法:

2. 母函数的定义

3. 例子
这里先给出2个例子,等会再结合题目分析:
第一种
有1克、2克、3克、4克的砝码各一枚,能称出哪几种重量?每种重量各有几种可能方案?
考虑用母函数来解决这个问题:
我们假设x表示砝码,x的指数表示砝码的重量,这样:
1个1克的砝码可以用函数 1 + 1 ∗ x 1 1+1*x^1 1+1∗x1表示,
1个2克的砝码可以用函数 1 + 1 ∗ x 2 1+1*x^2 1+1∗x2表示,
1个3克的砝码可以用函数 1 + 1 ∗ x 3 1+1*x^3 1+1∗x3表示,
1个4克的砝码可以用函数 1 + 1 ∗ x 4 1+1*x^4 1+1∗x4表示,
上面这四个式子懂吗?
我们拿 1 + x 2 1+x^2 1+x2来说,前面已经说过,x表示砝码,x的指数表示砝码的重量!初始状态时,这里就是一个质量为2的砝码。
那么前面的1表示什么?按照上面的理解,1其实应该写为: 1 ∗ x 0 1*x^0 1∗x0,即1代表重量为2的砝码数量为0个。
所以这里 1 + 1 x 2 = 1 x 0 + 1 x 2 1+1x^2 = 1x^0 + 1x^2 1+1x2=1x0+1x2,即表示2克的砝码有两种状态,不取或取,不取则为 1 x 0 1x^0 1x0,取则为 1 ∗ x 2 1*x^2 1∗x2
不知道大家理解没,我们这里结合前面那句话:
“把组合问题的加法法则和幂级数的乘幂对应起来“
接着讨论上面的 1 + x 2 1+x^2 1+x2,这里x前面的系数有什么意义?
这里的系数表示状态数(方案数)
1 + x 2 1+x^2 1+x2,也就是 1 x 0 + 1 x 2 1x^0 + 1x^2 1x0+1x2,也就是上面说的不取2克砝码,此时有1种状态;或者取2克砝码,此时也有1种状态。(分析!)
所以,前面说的那句话的意义大家可以理解了吧?
几种砝码的组合可以称重的情况,可以用以上几个函数的乘积表示:
( 1 + x ) ( 1 + x 2 ) ( 1 + x 3 ) ( 1 + x 4 ) (1+x)(1+x^2)(1+x^3)(1+x^4) (1+x)(1+x2)(1+x3)(1+x4)
= ( 1 + x + x 2 + x 4 ) ( 1 + x 3 + 4 + x 7 ) =(1+x+x^2+x^4)(1+x^3+^4+x^7) =(1+x+x2+x4)(1+x3+4+x7)
= 1 + x + x 2 + 2 x 3 + 2 x 4 + 2 x 5 + 2 x 6 + 2 ∗ x 7 + x 8 + x 9 + x 10 =1 + x + x^2 + 2x^3 + 2x^4 + 2x^5 + 2x^6 + 2*x^7 + x^8 + x^9 + x^{10} =1+x+x2+2x3+2x4+2x5+2x6+2∗x7+x8+x9+x10
从上面的函数知道:可称出从1克到10克,系数便是方案数。(!!!经典!!!)
例如右端有 2 x 5 2 x^5 2x5 项,即称出5克的方案有2种:5=3+2=4+1;同样,6=1+2+3=4+2;10=1+2+3+4。故称出6克的方案数有2种,称出10克的方案数有1种 。
第二种
接着上面,接下来是第二种情况:
求用1分、2分、3分的邮票贴出不同数值的方案数:
大家把这种情况和第一种比较有何区别?第一种每种是一个,而这里每种是无限的。

母函数图(4)
以展开后的 x 4 x^4 x4为例,其系数为4,即4拆分成1、2、3之和的拆分方案数为4;
即 : 4 = 1 + 1 + 1 + 1 = 1 + 1 + 2 = 1 + 3 = 2 + 2 4=1+1+1+1=1+1+2=1+3=2+2 4=1+1+1+1=1+1+2=1+3=2+2
这里再引出两个概念"整数拆分"和"拆分数":
所谓整数拆分即把整数分解成若干整数的和(相当于把n个无区别的球放到n个无标志的盒子,盒子允许空,也允许放多于一个球)。
整数拆分成若干整数的和,办法不一,不同拆分法的总数叫做拆分数。
现在以上面的第二种情况每种种类个数无限为例,给出模板
#include
using namespace std;
// Author: Tanky Woo
// www.wutianqi.com
const int _max = 10001;
// c1是保存各项质量砝码可以组合的数目
// c2是中间量,保存没一次的情况
int c1[_max], c2[_max];
int main()
{ //int n,i,j,k;
int nNum; //
int i, j, k;
while(cin >> nNum)
{
for(i=0; i<=nNum; ++i) // ---- ①
{
c1[i] = 1;
c2[i] = 0;
}
for(i=2; i<=nNum; ++i) // ----- ②
{
for(j=0; j<=nNum; ++j) // ----- ③
for(k=0; k+j<=nNum; k+=i) // ---- ④
{
c2[j+k] += c1[j];
}
for(j=0; j<=nNum; ++j) // ---- ⑤
{
c1[j] = c2[j];
c2[j] = 0;
}
}
cout << c1[nNum] << endl;
}
return 0;
}
我们来解释下上面标志的各个地方:(!!!重点!!!)
① 、首先对c1初始化,由第一个表达式 ( 1 + x + x 2 + . . x n ) (1+x+x^2+..x^n) (1+x+x2+..xn)初始化,把质量从0到n的所有砝码都初始化为1.
② 、 i从2到n遍历,这里i就是指第i个表达式,上面给出的第二种母函数关系式里,每一个括号括起来的就是一个表达式。
③、j 从0到n遍历,这里j就是(前面i個表达式累乘的表达式)里第j个变量。如 ( 1 + x ) ( 1 + x 2 ) ( 1 + x 3 ) (1+x)(1+x^2)(1+x^3) (1+x)(1+x2)(1+x3),j先指示的是1和x的系数,i=2执行完之后变为 ( 1 + x + x 2 + x 3 ) ( 1 + x 3 ) (1+x+x^2+x^3)(1+x^3) (1+x+x2+x3)(1+x3),这时候j应该指示的是合并后的第一个括号的四个变量的系数。
④ 、 k表示的是第j个指数,所以k每次增i(因为第i个表达式的增量是i)。
⑤ 、把c2的值赋给c1,而把c2初始化为0,因为c2每次是从一个表达式中开始的。
咱们赶快趁热打铁,来几道题目:
(相应题目解析均在相应的代码里分析)
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1028
代码:http://www.wutianqi.com/?p=587
这题大家看看简单不?把上面的模板理解了,这题就是小Case!
看看这题:
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1398
代码:http://www.wutianqi.com/?p=590
要说和前一题的区别,就只需要改2个地方。 在i遍历表达式时(可以参考我的资料—《母函数详解》),把i<=nNum改成了ii<=nNum,其次在k遍历指数时把k+=i变成了k+=ii; Ok,说来说去还是套模板~~~
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1085
代码:http://www.wutianqi.com/?p=592
这题终于变化了一点,但是万变不离其中。
大家好好分析下,结合代码就会懂了。
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1171
代码:http://www.wutianqi.com/?p=594
还有一些题目,大家有时间自己做做:
HDOJ:1709,1028、1709、1085、1171、1398、2069、2152
(原创文章,欢迎各位转载,但是请不要任意删除文章中链接,请自觉尊重文章版权,违法必究,谢谢合作。Tanky Woo原创, www.WuTianQi.com)
附:
1.在维基百科里讲到了普通母函數、指數母函數、L級數、貝爾級數和狄利克雷級數:
http://zh.wikipedia.org/zh-tw/%E6%AF%8D%E5%87%BD%E6%95%B0
2.Matrix67大牛那有篇文章:什么是生成函数:
http://www.matrix67.com/blog/archives/120
3.大家可以看看杭电的ACM课件的母函数那篇,我这里的图片以及一些内容都引至那。
如果大家有问题或者资料里的内容有错误,可以留言给出,博客:http://www.wutianqi.com/
Tanky Woo原创文章,转载请注明出处:http://www.wutianqi.com/?p=596。
对于任何转载本博客文章且不保留原文链接或任意删改文中链接的行为,本人将一定周旋到底!
老版下载地址:
母函数(Generating function)详解(点击下载)
(仅作保留所用,里面有错误,建议看我的最新版本,关注本博客:http://www.wutianqi.com/?p=539)
4. 矩母函数(Moment Generating Function)
“我们需要更多的特征来描述分布,例如峰度,偏度,除了常用的平均值,方差,这些特征统一称为矩,那么有没有一个函数能够计算所有矩呢?当然有,矩母函数,你就可以通过微分来计算各种矩,而不是从定义的积分算,你肯定知道微分比积分容易吧!”
https://blog.csdn.net/Anne033/article/details/109304935
4.1 概率统计中的“矩”是什么?
对比物理的力矩,你会发现,概率论中的“矩”真的是很有启发性的一个词。
4.1.1 力矩
大家应该都知道物理中的力矩,我这里也不展开说细节了,用一幅图来帮助大家回忆一下:

4.1.2 概率论中的“矩”
在概率论中,有一杆无处不在的“秤”。因为这把“秤”的存在,所以我们有了“矩”。
4.1.2.1 彩票的问题
福利彩票,,每一注两元钱,真是中国的良心啊,猪肉、房价都涨了多少了!?
每一注的中奖几率如下(胡诌的):

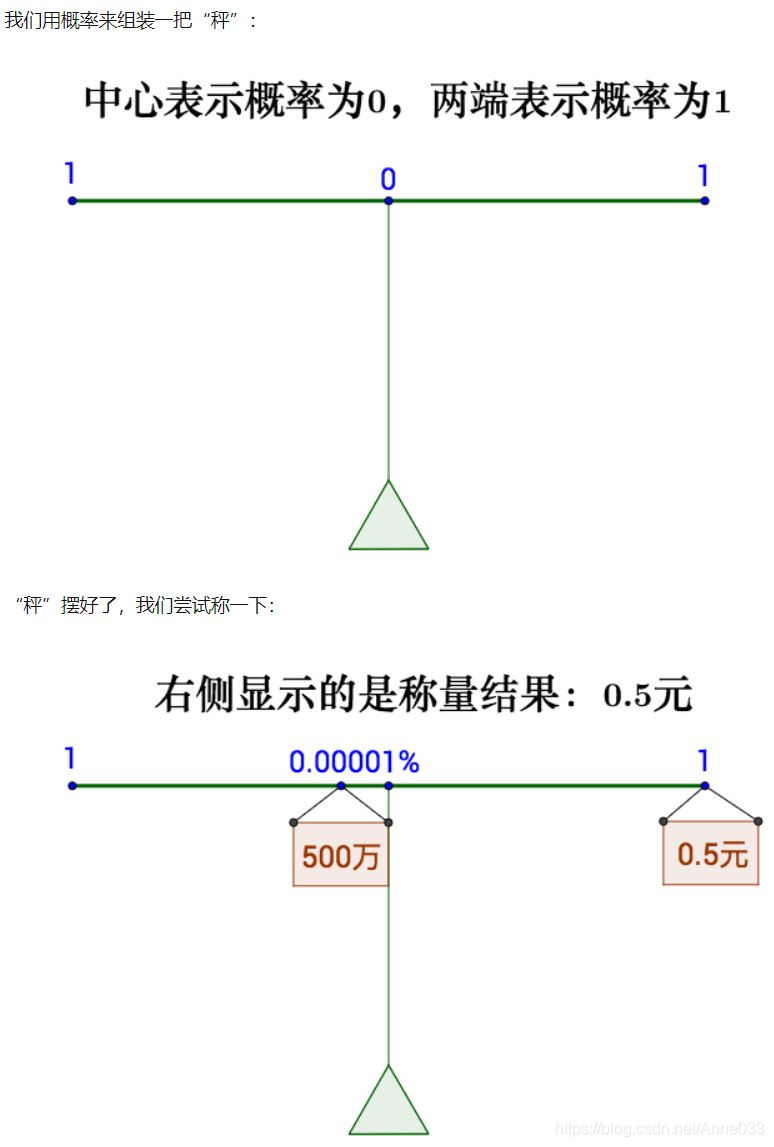
称量实际上是:


4.1.3 “矩”

%%%
比方说,我们感兴趣的是随机变量X。 矩是X的期望值,例如E(X),E(X²),E(X³)等。 第一矩是E(X), 第二矩是E(X²), 第三矩是E(X³), … 第n个矩是E(X ^ n)。
当然,我们非常熟悉前两个矩,均值μ= E(X)和方差E(X²)−μ²。它们是X的重要特征。 平均值是 平均值,方差是分布的分布程度。但是,必须有其他的特征来定义分布。例如,第三矩是分布的不对称性。第四关是尾巴有多沉、多厚。

这些矩告诉您有关分布的信息。
4.2 什么是矩产生函数(MGF)?
关于产生/母函数https://blog.csdn.net/Anne033/article/details/109652192
顾名思义,MGF实际上是生成矩的函数 E(X),E(X²),E(X³),…,E(X ^ n)。也就是”矩“的母亲,够通俗吧。


这就是您从MGF那里获取时光的方式。

4.3 证明,为什么第n个矩是MGF的第n个导数?
我们将使用泰勒级数证明这一点。

如果对③取另一种导数(因此取两次),则将得到E(X²)。 如果您采用另一个(三阶)导数,则将得到E(X³),依此类推…… 当我第一次看到矩生成函数时,我无法理解t在函数中的作用,因为t似乎是我不感兴趣的任意变量。但是,如您所见,t是辅助变量。我们引入t是为了能够使用演算(导数)并使(我们不感兴趣的)项为零。 等等…
但是我们可以直接了当,使用期望值的定义来计算。为什么我们还需要MGF?
4.4 为什么我们需要MGF?
为了方便,当然是我们希望MGF可以轻松计算矩。 但是,为什么MGF比定义期望值更容易? 在我的数学教科书中,他们总是问我“请找出计算二项式(n, p),泊松(λ),指数(λ),正态(0, 1)等的函数的矩。” 但是,他们从未真正向我展示过为什么MGF会如此有用以至于它们激发喜悦。
我认为以下示例会给您带来喜悦,最简单的示例显示MGF更容易:指数分布的MGF。
我们将从PDF开始。

指数分布的PDF

导出指数的MGF。

对于存在的MGF,应该存在期望值 E ( e t x ) E(e ^ tx) E(etx)。 这就是为什么“ t-λ<0”是要满足的重要条件的原因,因为,不满足积分将不会收敛。(这称为散度检验,这是在尝试确定积分是收敛还是发散时首先要检查的内容。) 一旦有了MGF: λ / ( λ − t ) λ/(λ-t) λ/(λ−t),计算矩就变成了求导数的问题,这比积分更容易直接计算期望值。
使用MGF,可以通过求导数而不是积分来查找矩!
4.5 常见分布的MGF
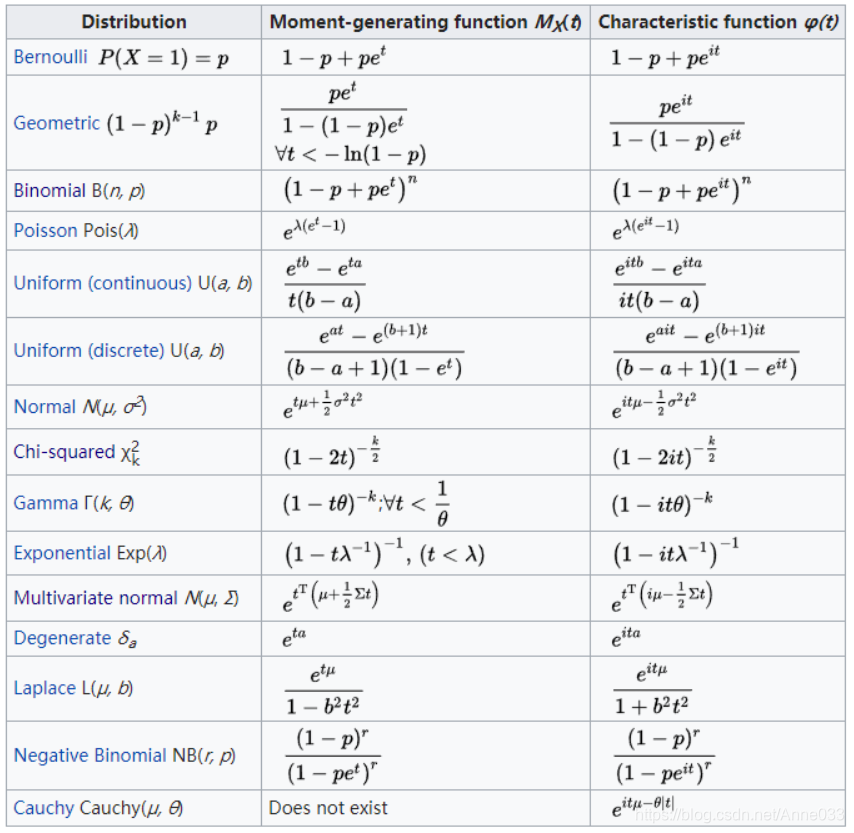
4.6 MGF的属性

注意事项
对于任何有效的MGF,M(0)= 1,每当您计算MGF时,插入t = 0并查看是否得到1。
矩提供了一种指定分布的方法。例如,您可以在前两个矩(均值和方差)完全指定正态分布。当您知道分布的多个不同矩时,您将了解有关该分布的更多信息。如果有一个您没有认识的人,并且您知道他们的身高,体重,肤色,喜爱的爱好等,您仍然不一定完全了解他们,但是正在获得关于他们的越来越多的信息。
MGF的优点在于,一旦有了MGF(一旦存在期望值),您就可以得到第n个矩。MGF将随机变量的所有矩编码为一个函数,以后可以再次从中提取它们。
概率分布由其MGF唯一确定。如果两个随机变量具有相同的MGF,则它们必须具有相同的分布。
对于那些对术语“矩”感到好奇的人(像我一样):为什么一个矩称为矩?
分布的重要特征之一是它的尾巴有多沉重,尤其是对于金融风险管理而言。如果您还记得2009年的金融危机,那实际上就是无法解决罕见事件发生的可能性。风险管理人员低估了基金交易头寸中的许多金融证券的峰度(峰度在希腊语中是指“凸起”)。有时,假设的风险曲线平滑的随机分布可能会在其中隐藏凸起。而且我们可以检测到使用MGF的人员!
https://zhuanlan.zhihu.com/p/148408669
https://en.wikipedia.org/wiki/Moment-generating_function
http://www.wutianqi.com/blog/596.html
https://zhuanlan.zhihu.com/p/148408669