说在前面的话：如果所有的边权都不相等，那么求得的最小生成树是唯一的。

难度：无向图求最小生成树 << 有向图求最小生成树

最小生成树是对于无向图来说的，有向图的所有顶点最短连接叫做最小树形图。难度增加在：1）消除回路（不仅是多顶点回路，双顶点回路也要考虑）。2）边的方向要一致（不能让某个顶点既有出边又有入边）。

生长法（Kruskal algorithm）

生长法（克鲁斯卡尔算法）是一步步地将森林中的树进行合并。

之所以叫他生长法，是因为它算法思想包含一个从小到大的过程。首先按照边的权值进行从小到大排序，然后从小到大开始选边，注意不能构成回路，逐个判断后加入到生成树中，直到加入了n-1条边为止。

测试程序：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
struct node
{
    int x;
    int y;
    int z;
}nd[100];
bool cmp(struct node a,struct node b)
{
    return a.z<b.z;
}
int f[100];
int get(int x)
{
    if(f[x]==x)
        return x;
    else
    {
        f[x]=get(f[x]);
        return f[x];
    }
}

int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d %d %d",&nd[i].x,&nd[i].y,&nd[i].z);
    }
    for(int i=1;i<=n;i++)
        f[i]=i;
    sort(nd+1,nd+m+1,cmp);
    int sum=0;
    for(int i=1;i<=m;i++)
    {
        if(get(nd[i].x)!=get(nd[i].y))
        {
             cout<<nd[i].x<<"  "<<nd[i].y<<"  "<<nd[i].z<<endl;
            f[get(nd[i].y)]=get(nd[i].x);
            sum+=nd[i].z;
            cout<<sum<<endl;
            if(i==n-1)
                break;
        }

    }
    cout<<sum<<endl;
}

测试结果：

M: 边数 N:元素个数

时间复杂度： sort $O(Mlog_{2}M)$ 构建最小生成树需要 $O(Mlog_{2}(N))$ 所以时间复杂度为： $O(O(Mlog_{2}M)+O(Mlog_{2}N))$ ,因为M>>N，所以一般为 $O(Mlog_{2}M)$ 。

因为和边有关，所以适用求边比较少的网（稀疏图）的最小生成树。

近水楼台先得月法（Prim）

近水楼台先得月法是通过每次增加一条边来建立一棵树。

算法思想：因为最后求得的最小生成树肯定囊括了所有的顶点。所以可以选任意一个顶点作为开始，逐渐壮大最小生成树。依次找到距离最小生成树最近的非树顶点，加入到树中，直到最小生成树建立好。

邻接矩阵好操作一些，不过时间复杂度比较高 $O(N^{^{2}})$ 。这个和求单源最短路的边松弛法比较像，不过源点不是一个，生成树中所有的点都是源点。

测试程序：

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int map[100][100];
int dis[100];
int book[100];
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=99999999;
        }
    }
    for(int i=1; i<=n; i++)
    {
        if(i==1)
            dis[i]=0;
        else
            dis[i]=99999999;
    }
    for(int i=1; i<=m; i++)
    {
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        map[a][b]=c;
        map[b][a]=c;
    }
    int minn=99999999;
    int sum=0;
    int j;
    book[1]=1;
    for(int i=1; i<=n; i++)
    {
        if(map[1][i]<dis[i])
            dis[i]=map[1][i];
    }
    for(int i=1; i<=n-1; i++)
    {
        minn=99999999;
        for(int i=1; i<=n; i++)
        {
            if(dis[i]<minn&&book[i]==0)
            {
                minn=dis[i];
                j=i;
            }
        }
        book[j]=1;
        sum+=minn;
        for(int i=1; i<=n; i++)
        {
            if(book[i]==0)
            {
                if(map[j][i]<dis[i])
                    dis[i]=map[j][i];
            }
        }
    }
    cout<<sum<<endl;

}

测试结果：

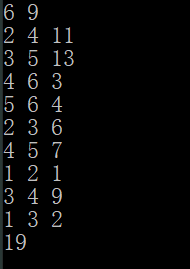
如果除去无向图的性质，将边改为有向图（即2 4 认为2->4 4->2 认为不可达），结果为：

如果双向均认为可达，结果为：

差别在于最小生成树选择可达5号端点的路径由 4-5 7 这个改为了 5-6 4 ，结果由22->19。

所以无向图求最小生成树的时候一定要记得是双向可达的。

算法之所以优秀，是因为可以优化，不优化的程序实际上没有参考的意义。

如果借助堆，每次选边时间复杂度为 $O(log_{2}M)$ ，使用邻接表来存储图的话，整个算法的时间复杂度会降低到 $O(Mlog_{2}N)_$

测试程序：

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int n,m,size;
int u[100],v[100],w[100];
int first[100],next[100];
int dis[100];
int sum;
int book[100];
int stack_num[100];
int stack_pos[100];
void sift_up(int i)
{
    if(i/2>=1)
    {
        if(dis[stack_num[i]]<dis[stack_num[i/2]])
        {
            swap(stack_num[i],stack_num[i/2]);
            swap(stack_pos[stack_num[i]],stack_pos[stack_num[i/2]]);
            i=i/2;
        }
        else
            return;
    }
}
void sift_down(int i)
{
    int t=i;
    int t1=i;   
    while(t*2<=size)
    {
        if(t*2<=size)
        {
            if(dis[stack_num[t]]>dis[stack_num[t*2]])
                t1=t*2;
        }
        if(t*2+1<=size)
        {
            if(dis[stack_num[t1]]>dis[stack_num[t*2+1]])
                t1=t*2+1;
        }
        if(t1==t)
            break;
        else
        {
            swap(stack_num[t],stack_num[t1]);
            swap(stack_pos[stack_num[t]],stack_pos[stack_num[t1]]);
            t=t1;
        }
    }
}
int pop()
{
    int i=stack_num[1];
    stack_num[1]=stack_num[size];
    size--;
    stack_pos[stack_num[1]]=1;
    sift_down(stack_pos[stack_num[1]]);
    cout<<"i="<<i<<endl;
    return i;
}
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1; i<=2*m; i++)
    {
        first[i]=-1;
        next[i]=-1;
    }

    for(int i=1; i<=m; i++)
    {
        scanf("%d %d %d",&u[i],&v[i],&w[i]);
        u[i+m]=v[i];
        v[i+m]=u[i];
        w[i+m]=w[i];
    }

    for(int i=1; i<=2*m; i++)
    {
        if(first[u[i]]==-1)
            first[u[i]]=i;
        else
        {
            next[i]=first[u[i]];
            first[u[i]]=i;
        }
    }

    for(int i=1; i<=n; i++)
        dis[i]=99999999;

    dis[1]=0;
    book[1]=1;
    int t;
    t=first[1];
    while(t!=-1)
    {
        if(book[t]==0)
        {
            dis[v[t]]=w[t];
        }
        t=next[t];
    }

    for(int i=1; i<=n; i++)
    {
        stack_num[i]=i;
        stack_pos[i]=i;
    }

    int j;
    size=n;

    for(int i=n/2; i>=1; i--)
    {
        sift_down(i);
    }
    pop();

    int count=1;
    while(count<=n-1)
    {
        int j=pop();
        book[j]=1;
        count++;
        sum+=dis[j];
        cout<<"sum="<<sum<<endl;
        int t=first[j];
        while(t!=-1)
        {
            if(book[v[t]]==0)
            {
                if(dis[v[t]]>w[t])
                {
                    dis[v[t]]=w[t];
                    sift_up(stack_pos[v[t]]);
                }
            }
            t=next[t];
        }

    }

    cout<<"sum="<<sum<<endl;


}

测试结果：

思路：

时间复杂度严格来说应该是： < $\large O(N*M*log_{2}N)$ 很显然，它适合稀疏图。 M越接近N，这个算法越不划算。

将邻接表存储边和堆排序选边结合起来的算法耗时如下：

使用邻接矩阵的程序耗时如下：

所以综上可以看出，使用邻接矩阵耗时更少一些，所以算法的优劣是看所处的环境是否有利于自己。不能简单的说这个好，那个不好。

求最小生成树的两种简单算法（生长法、近水楼台先得月法）

说在前面的话：如果所有的边权都不相等，那么求得的最小生成树是唯一的。

猜你喜欢