Make Your Own Neural Network
构建你自己的神经网络
作者:lz0499
声明:
1)Make Your Own Neural Network翻译自Tariq Rashid编写的神经网络入门书籍。作者的目的是尽可能的少用术语和高深的数学知识,以图文并茂的方式讲解神经网络是如何工作的。任何拥有高中数学水平的人就能够理解神经网络的工作方式。强烈推荐初学者以这本书作为神经网络入门书籍。
2)本文仅供学术交流,非商用。翻译的初衷是一边翻译一边加深对神经网络的理解。
3)由于刚刚接触神经网络这方面的知识,翻译过程中难免有些错误。若发现错误,还请各位前辈指正。谢谢!
4)由于工作原因,我将有选择的按照原文的章节不定期的进行翻译更新。
5)此属于第一版本,若有错误,还需继续修正与增删。
目录:
第一部分:神经网络是如何工作的
实际上是如何更新权重(一)
至此,我们通过反向传输法把误差传回至各层神经网络。为什么需要这么做呢?因为我们想利用误差来指导如何修改神经网络各层的权重值以使输出结果接近训练值。这也是我们开头第一小节构建线性分类器的基本思想。
但是,神经网络中的节点并不像线性分类器这么简单。这些节点把前一神经网络层的输入信号做加权和,然周再应用于sigmoid激活函数,输出最终的结果。因此,我们该如何更新神经网络中的权重呢?我们难道不能使用线性代数的方法直接计算出需要更新的权重值?
实际上,我们确实不能通过线性代数的方法直接计算出需要更新的权重值。因为用线性代数的方法计算权重值太复杂了,需要涉及到太多权重的组合,太多函数的函数的函数组合。想想一下,之前我们构建的每层三个节点共三层网络的简单神经网络,我们如何修改输入层的节点与隐藏层节点之间的权重,以使得神经网络输出层的结果增加了,比如说增加0.5?即便是我们够幸运,使得输出层的第一个节点增加了0.5,但是当我们需要需该另外一个输出节点的结果时,可能会影响到第一个输出节点的,又会把第一个输出节点的值更改为其他非0.5的数值。这么做将无法得到正确的结果。
如果你想象不到有多么复杂,那么可以观察如下式子。下式表示的是每层三个节点共三层的神经网络层输出结果,其结果是输入信号和神经网络层之间权重的一个函数。输入层的第i个输入信号为xi,隐藏层第j个节点与输入层第i个节点之间的权重为wi.j。同样的,隐藏层第j个节点的输出为xj,其与输出层第k个节点之间的权重值为wj,k。求和表达式表示的是把a到b的区间之间的所有值相加求和。即我们可以得出输出层第k个节点的输出为:
嗯哼。公式够复杂的!!
我们是否能够通过权重的简单随机组合找到我们想要的值呢?嗯,这个也太随机了吧!不知道要算到什么时候才能得到我们想要的结果!!
不用随机值,那么我们是否可以通过暴力组合的方法,把权重的所有组合都遍历一边直到找到我们想要的结果呢?尽管这个暴力遍历的方法可能破解简单的英文密码,但是想象一下-1到1权重范围的每一个权重都有1000中可能,比如说0.501,-0.203,0.999等等,那么对于每层三个节点共三层的简单神经网络,每一层将有1个权重,所以每一层有18000中可能的权重组合。如果我们有一个每层500个节点的典型神经网络,那么每一层权重的组合将达到500000种,如果每一种权重组合需要一秒钟构建,那么,我们将花费16年的时间更新其中的一个训练数据的权重组合,如果需要1000个训练数据对神经网络进行训练,那么我们得到神经网络最后结果时,我们已经耗费了16000年了!!My God!
这计算时间也忒长了吧!!
从上面的推算可知,暴力法并对神经网络一点也不实用。事实上,当神经网络层不断增加时,其暴力搜索的方法更加糟糕。
直到十九世纪六七十年代,数学家才解决这个困惑世人数十年的难题。究竟是谁第一个解决这个难题,世人众说纷纭。但重要的是,这一迟来的发现导致现代神经网络能解决一些令人惊讶的任务。
那么,我们究竟该如何解决这个难题了?不管你信不信,你已经拥有了解决这个难题的工具了。我们将在后续细细道来。
用数学表达式计算神经网络的输出太复杂了。需要一个一个测试不同权重的组合直到找到最佳权重值。事实上,在训练神经网络时,训练数据有可能并不够充分;并且训练数据也可能存在一些误差;亦或是神经网络并没有足够的神经网络层和节点用于求解正确的结果。
我们是否可以使用一种计较现实的方法,虽然这种方法不能用数学公式很好的表示出来,但是通过这种方法我们能够得的一个比较好的近似的结果。这也是不错的。
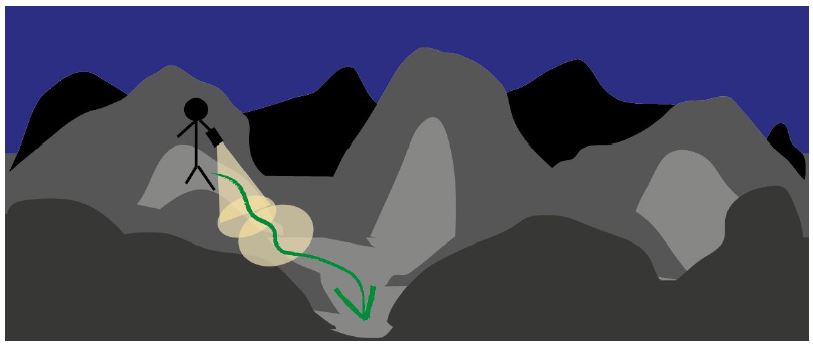
想象一块有许多山峰和山谷的非常复杂的地形,山与山之间有曲折的小路相连。此时此刻,天完全黑下来了,你基本上什么也看不清楚。你只知道你在山峰的一侧,你想要迅速走到山谷中。你甚至没有一幅该地详细的地图,有的只是一只残旧的手电筒,而且手电筒将随时没电,你必须迅速行动起来。你该怎么办呢?你可能会用你的手电筒照射离你最近的地方,看看是不是有向山下走的小路,并朝着这个方向前进一小步。用这种方法,即使你没有该地的地图也没有在该地旅游过,你也可以一步一步渐渐向山谷靠拢。
这种方法在数学上被称为梯度下降法。从上述图示中你也可以知道为什么回叫做梯度下降法。走了一小步之后,你继续查看附近区域看是否哪个方向能够更加靠近你的目的地,之后你再向这个方向靠近一步。如此反复直到你高兴的达到了你打算前往的山谷。这个梯度就涉及到地形的一个斜率,你需要前进的那个方向就是该地地形最为陡峭的方法。
现在想象一下这个复杂的地形是一个数学函数。那么,即使在我们不能够很好的理解这个复杂函数计算出最小值的时候,梯度下降法怎样才能为我们找到这个函数的最小值呢?如果一个函数太复杂,以至于我们不能用一种简单的线性代数的方法找到其最小值,我们就可以尝试使用梯度下降法找到该函数的最小值。可能使用梯度下降法找到的最终结果并不是该函数的最准确的结果,但是总比没找到结果的好。无论如何,我们可以按照最小步进调整答案,直到它基本靠近真实的最小值为止。
这么酷的梯度下降法与神经网络究竟有什么联系呢?如果梯度下降法中的复杂函数时神经网络输出的误差,那么找到函数的最小值就相当找到了神经网络中误差的最小值,也即是使得神经网络的输出值最接近甚至等于训练样本数据值。这就是我们需要做的。
让我们用梯度下降法实际计算一个超级简单函数,使我们更加直观的理解梯度下降法。
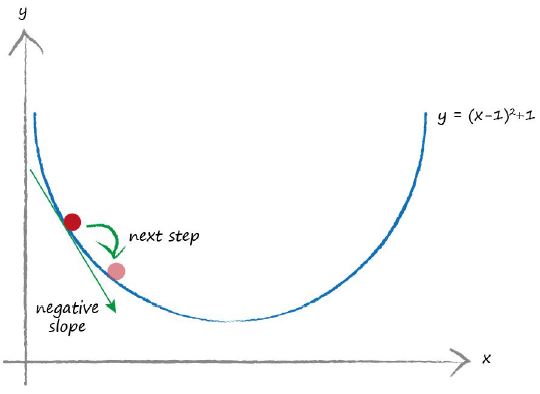
下图表示的是简单函数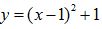
我们从任意位置开始实施梯度下降法。上图中我们从随机从一个位置开始,就像之前描述的那样,我们开始向下下山。首先我们观察我们所在位置哪个方向是向下的。上图中标记的斜率是是一个负值。我们沿着向下的方向继续前进,所以我们应该沿着x轴向右继续前进。因此,我们把x增加一点点。我们可以观察到我们向右移动了一点点,使得我们更加靠近真实的最小值。
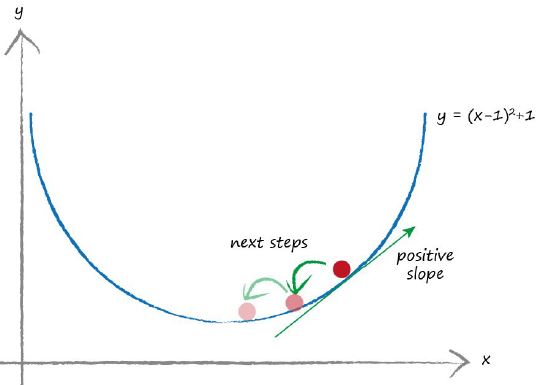
让我们假设从另外一个位置开始。如下图所示。
这次斜率为正值,所以我们向左开始移动。即减小变量x一点点。我们可以再一次看到我们向着实际的最小值靠近了。我们可以继续这种步骤,直到我们计算出来的值与实际的最小值在可容忍的误差范围内。
必要的一步是修正移动的步进,避免超过最小值而总是在最小值周围震荡。我们可以想象我们与实际的最小值只相差0.5米,但是我们最小步长是2米。如果我们继续沿着原来的方向修改位置,那么我们将超过最小值的位置。如果在靠近最小值位置的时候缓慢的修改x的位置,即使用最小梯度法计算出的步长,那么我们能够合理的靠近最小值位置。这是基于越靠近最小值斜率越小的假设。这种假设对大多数平滑的连续函数而言还不错。
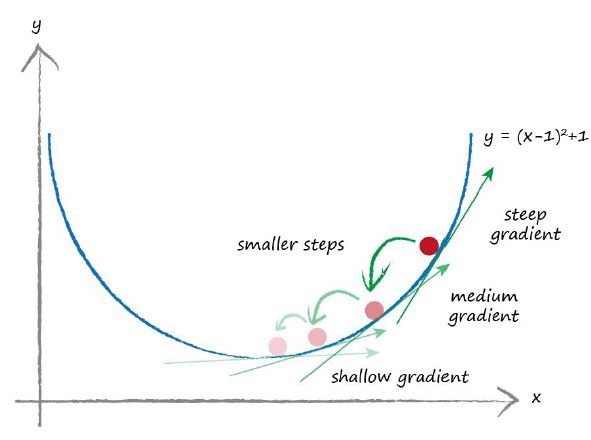
下图表示的是当函数的梯度越来越小时,我们也更加平缓的靠近最小值位置。
顺便说下,不知道你们观察到没有,我们是按照梯度反方向修改x的位置。正的梯度我们减小x,负的梯度我们增加x.就像图中标注的那样,但是我们比较容易忘记这么修改,再次提醒大家一下。
当我们使用梯度下降法求解最小值的时候,我们并没有用代数的方法真正求得最小值,因为我们假设函数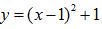
当一个函数拥有非常多的参数时,梯度下降法将大显身手。假设y不仅仅取决于x,它还取决于a,b,c,d,e和f。想象这么一种函数,比如说神经网络中的误差函数,误差函数的最后结果取决于神经网络层中非常多的权重参数(一般来说都有100个左右)。
我们可以观察如下一个三维地理空间,想知道梯度下降法是否会带领我们到达最低的一个山谷中。实际上,梯度下降法有时候会卡在一个错误的山谷中,这个山谷可能并不是最低的山谷。对于非常复杂的函数而言,会有很多局部最小值,也就是对于上面三维地图中的非最低山谷,那么,如何才能避免落入到非最低山谷中呢?
为了避免落入到错误的山谷中或者说函数最小值,我们从山顶的不同位置开始训练我们的神经网络,以保证我们不会总是落入到错误的山谷中。不同起始点意味着使用不同的初始化参数,对于神经网络来说,就是使用不同的初始权重值。
下面三个图表示的是沿着梯度下降法中的方向调整位置,其中中间那个落入了错误的山谷位置。