题目描述
现有一块大奶酪,它的高度为 hh,它的长度和宽度我们可以认为是无限大的,奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系,在坐标系中,奶酪的下表面为 z = 0,奶酪的上表面为 z = h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在不破坏奶酪的情况下,能否利用已有的空洞跑 到奶酪的上表面去?
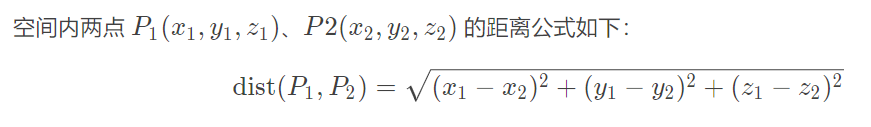
输入格式

输出格式

输入样例
3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4
输出样例
Yes
No
Yes
说明/提示

数据规模

AC代码
#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1005;
ll n,h,r;
struct xy{
ll x,y,z;
}a[maxn];
inline bool cmp(const xy &z1,const xy &z2){
return z1.z < z2.z;
}
inline bool isOk(const xy &z1,const xy &z2){
if(sqrt((z1.x-z2.x)*(z1.x-z2.x)+(z1.y-z2.y)*(z1.y-z2.y)+(z1.z-z2.z)*(z1.z-z2.z)) <= 2*r){
return true;
}
return false;
}
bool isAlright = false;
void solve(xy x,ll s,ll g){
if(g + r >= h){
isAlright = true;
}
for(ll i=s;i<=n;i++){
if(a[i].z - x.z > 2*r || isAlright) break;
else{
if(isOk(x,a[i])){
solve(a[i],i+1,a[i].z);
}
}
}
}
int main()
{
int T;
cin>>T;
while(T --){
isAlright = false;
cin>>n>>h>>r;
for(ll i=1;i<=n;i++){
cin>>a[i].x>>a[i].y>>a[i].z;
}
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++){
if(a[i].z - r <= 0 && !isAlright){
solve(a[i],i+1,a[i].z);
}
}
if(!isAlright){
cout<<"No";
}
else{
cout<<"Yes";
}
cout<<endl;
}
return 0;
}
送大家两组测试数据
6
2 1000 250
0 0 250
0 0 751
2 1000 400
400 750 5
840 716 718
3 2000 600
328 1454 1005
114 736 1503
860 131 556
4 5000 1000
1249 4828 4646
4638 2770 880
289 267 2924
142 2875 3957
5 1060 300
634 586 1008
756 332 385
570 40 776
428 176 380
695 1028 36
6 8765 4321
2468 2920 3602
613 6875 33
1935 230 809
4916 7853 4995
5960 1560 2989
1758 4793 6410
No
No
No
No
No
Yes
5
1 100 60
70 27 88
1 100 75
80 39 34
1 100 50
605 563 50
1 200 160
120 176 40
1 200 10
50 47 84
No
Yes
Yes
Yes
No
解释
①本题用并查集,广搜和深搜都能解,本人在这里用的是深搜。
②看懂题是很关键的,题目明确说了Jerry从(0,0,0)开始走,意味着如果没有球域可以包括(0,0,0)这个点,那Jerry是走不动的,直接输出No即可。
③深搜:
bool isAlright = false;
void solve(xy x,ll s,ll g){
if(g + r >= h){
isAlright = true;
}
for(ll i=s;i<=n;i++){
if(a[i].z - x.z > 2*r || isAlright) break;
else{
if(isOk(x,a[i])){
solve(a[i],i+1,a[i].z);
}
}
}
}
说实话,这个深搜的思路毫无特色,不难想,本人使用一个变量s替代了vis布尔数组,省略了判断这个点是否来过的步骤,因为输入之后我们已经按照球域的高度对球心进行了排序,故每到一个球心,在存储球心坐标的数组中,下一个球心坐标的z值(高度)一定比当前球心高(或相等,倘若深搜一条路无法到达终点,可以从同高度的另一条路另辟蹊径)。
④剪枝: 剪枝当属本题的一大特色了,代码中两次用到剪枝,否则后面的测试点统统都会TLE。
第一次用到剪枝,进入solve函数之前:
for(int i=1;i<=n;i++){
if(a[i].z - r <= 0 && !isAlright){
//这一步用到了剪枝
solve(a[i],i+1,a[i].z);
}
}
这一步:if(a[i].z - r <= 0 && !isAlright),即如果这个球心所在的球域不包括原点,则跳过,如果已经找到一条出路,则结束判断。
第二次用到剪枝,solve函数中:
for(ll i=s;i<=n;i++){
if(a[i].z - x.z > 2*r || isAlright) break;//这一步用到了剪枝
else{
if(isOk(x,a[i])){
solve(a[i],i+1,a[i].z);
}
}
}
即:if(a[i].z - x.z > 2*r || isAlright) break;如果当前所在球心不能到达下一个球域,结束循环,或如果已经找到出路,结束循环。
⑤AC。