嘿大家,我又回来了,今天我们来介绍一下并查集,它是一种很高效的算法,值得学习
现在,我们先看看一道题,简单思考一下。
引入
如题,现在有一个并查集,你需要完成合并和查询操作。
输入输出格式
输入格式:
第一行包含两个整数N、M,表示共有N个元素和M个操作。
接下来M行,每行包含三个整数Zi、Xi、Yi
当Zi=1时,将Xi与Yi所在的集合合并
当Zi=2时,输出Xi与Yi是否在同一集合内,是的话输出Y;否则话输出N
输出格式:
如上,对于每一个Zi=2的操作,都有一行输出,每行包含一个大写字母,为Y或者N
输入输出样例
输入样例#1:
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
输出样例#1:
N
Y
N
Y
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据,N<=10,M<=20;
对于70%的数据,N<=100,M<=1000;
对于100%的数据,N<=10000,M<=200000。
一、思考
看完题目,你可能一头雾水,也可能灵光乍现,我们就先来了解一下什么是并查集:
并查集被很多OIer认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:
合并(Union):把两个不相交的集合合并为一个集合。
查询(Find):查询两个元素是否在同一个集合中。
是的,我们可以把并查集理解成是一种集合数据库,里面记录了集合之间的关系。这样说未免让人摸不着头,我们就先来引入一个实际问题
现在有5个人,名叫1,2,3,4,5,他们有各自的老大(老大可以是自己),现在规定,1,2,3共用一个老大,4,5共用一个老大(或者说是共用一个组),我们可以如何表示呢?
是的,我们当然可以把1,2,3存入一个数组叫a,把4,5存入一个数组叫b,但这样未免慢了些,有什么快捷的方法吗?有的,并查集
我们先设置一个数组名叫p,如果要实现用一条数组存储这样的关系,我们可以规定1,2,3的老大是1,4和5的老大是4,那么如果将p的下标定义为人员,内部存的数据定为它的老大,是不是就可以得到这个关系了呢?没错,得到的p就是[1,1,1,4,4](下标从1到5)。
我们执行查询的时候,比如说我要知道3的老大是谁,我只需要调用p[3],里面存的就是集合头子。
好的,现在我们已经介绍了查询了,如何合并呢?聪明的你一定想到了,如果我要合并上述第一个和第二个集合,我只需要把第二个集合的内容都改成第一个的头子即可。
二、具体实现
这里find()函数我们要单独拎出来讲讲:
int f[10005];
int find(int k){
return f[k]==k?k:f[k] = find(f[k]);
}
我们注意到find是这样运作的:
1.如果找到的f数组内容就是本身查询的k值(自己就是自己的头子,相当于上述例子p[1]=1),则直接返回k值
2.如果不是,就要去更深层挖掘,也就是我们写的递归程序,令f[k] = find(f[k]),一方面在寻找k的总头子(头子也可能有头子),一方面也直接把找到的值赋给了f[k],我们管这叫路径压缩
(路径压缩优化后,并查集的时间复杂度已经比较低了,绝大多数不相交集合的合并查询问题都能够解决)
代码如下(示例):
#include<bits/stdc++.h>
using namespace std;
int f[10005];
int find(int k){
if(f[k]==k)return k;
else return f[k] = find(f[k]);
}
int main(){
int n,m;
cin >> n >> m;
for(int i=1;i<=n;i++)f[i] = i;
int type,a,b;
while(m--)
{
scanf("%d%d%d",&type,&a,&b);
if(type==1){
f[find(b)] = find(a);
}else
{
if(find(b)==find(a))
cout << "Y" << endl;
else
cout << "N" << endl;
}
}
return 0;
}
三、拓展题
ZCMU-1435
盟国
Time Limit: 3 Sec Memory Limit: 128 MB
Submit: 592 Solved: 143
世界上存在着N个国家,简单起见,编号从0~N-1,假如a国和b国是盟国,b国和c国是盟国,那么a国和c国也是盟国。另外每个国家都有权宣布退盟(注意,退盟后还可以再结盟)。
定义下面两个操作:
“M X Y” :X国和Y国结盟 (如果X与Z结盟,Y与Z结盟,那么X与Y也自动结盟).
“S X” :X国宣布退盟 (如果X与Z结盟,Y与Z结盟,Z退盟,那么X与Y还是联盟).
Input
多组case。
每组case输入一个N和M (1 ≤ N ≤ 100000 , 1 ≤ M ≤ 1000000),N是国家数,M是操作数。
接下来输入M行操作
当N=0,M=0时,结束输入
Output
对每组case输出最终有多少个联盟(如果一个国家不与任何国家联盟,它也算一个独立的联盟),格式见样例。
Sample Input
5 6
M 0 1
M 1 2
M 1 3
S 1
M 1 2
S 3
3 1
M 1 2
0 0
Sample Output
Case #1: 3
Case #2: 2
拓展题AC代码
在这里我就先上代码了,有能力的同学可以先看,看不懂的话下面我会解释
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6+5;
int f[maxn],ff[maxn],vis[10000];
int find(int k){
if(f[k]==k)return k;
else return f[k] = find(f[k]);
}
int main(){
int m,n,ca = 1;
while(~scanf("%d%d",&n,&m))
{
int pos = n;
if(m==0&&n==0)break;
for(int i=0;i<maxn;i++)f[i] = ff[i] = i;
while(m--){
char str[2];
int a,b;
scanf("%s %d",str,&a);
if(str[0]=='M'){
scanf("%d",&b);
int fa = find(ff[a]);
int fb = find(ff[b]);
if(fa!=fb)f[fa] = fb;
}else if(str[0]=='S')
{
ff[a] = pos;
f[pos] = pos;
pos++;
}
}
set<int>s;
for(int i=0;i<n;i++)
s.insert(find(ff[i]));
printf("Case #%d: %d\n",ca++,s.size());
}
return 0;
}
思路讲解
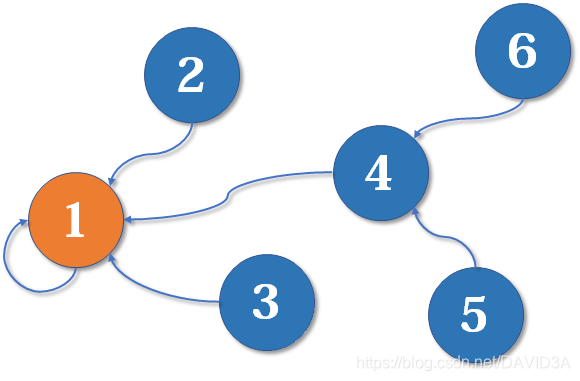
我们可以看到,现在这是一个关于数集合的树,可以得到一个关系,2,3,4的老大是1,5和6的老大是4,如果我们现在要实现删除的操作,我们该怎么做呢?
删除操作比合并操作稍微复杂一点。
首先,我们已经用f数组保存了原来结点间的关系(2,3,4的老大是1,5和6的老大是4),现在我们想要让4从这个关系图中剔除,我们就需要新建一个数组ff[],里面存储的就是最新的关系
也就是说,删除操作要这样执行
ff[a] = pos;
f[pos] = pos;
pos++;
//pos就是从n开始增大,因为题目数据范围是0 to n-1
我们首先让ff内的a指向pos,(pos已经在原有数据范围之外了),我们可以理解为a这个数据被流放了,同时在f数组执行f[pos] = pos,使得让pos的老大就是本身,这样在find运行时可以作为一个独立的个体
我们用一个形象的比喻:
澳大利亚是英国殖民时期的罪犯流放地,但刚开始并没有罪犯对吧。现在,英国本来有6个小混混,他们之间的关系如上图,现在4号小混混(小头子)放下了杀人罪,被法律规定要流放到澳大利亚,成为那里第一个犯人,于是,执行官(也就是ff数组把ff[4]=7标记了)把4送到了7这个地方流放了,也就是新开辟的澳大利亚区域,但是,尽管4号小头子被流放了,它两个手下5和6的总头子仍然是1,为了以后警察能通过f数组仍然找到最大的头子1,f数组原来数据范围内的数据是不会有变化的,只是会添加一条 f[pos] = pos,意味着如果澳大利亚警察找4的头子,那还是会找到4本身的。
接下来讲讲稍微简单的合并操作
int fa = find(ff[a]);
int fb = find(ff[b]);
if(fa!=fb)f[fa] = fb;
我们可以注意到,fa是在ff数组(最新的犯罪记录,用了上面的例子了)里用find函数查找a的头子(注意:find函数用的还是f数组,原因上面已经讲过了),fb同理,如果头子相同,那么不必执行操作,如果不同,就要在f数组里面记录a的头子就是b的头子(其实反过来也是对的)
总结
今天介绍了了并查集的简单入门,查询,合并和删改,并做到了一些应用,后面那个例子讲的可能不是非常恰当,但希望能帮助你理解。
如有出错,希望在评论区告知,希望能给你们派上用场。