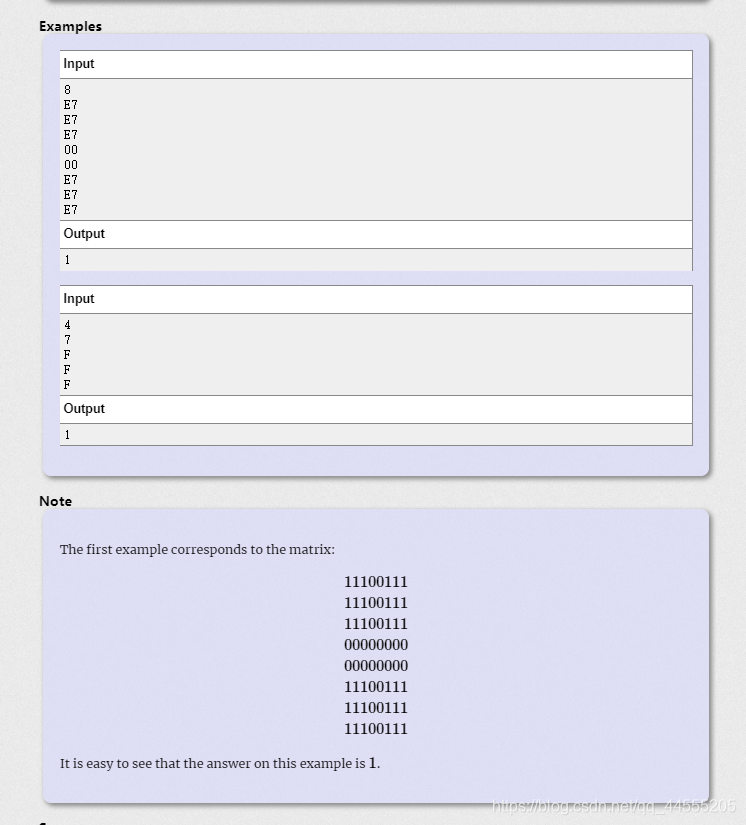
题意：给你二维A矩阵，在满足条件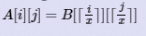
的情况下问x的最大值；
千万注意B这个二维矩阵是压缩过后的矩阵，为什么这样说：
比如:
88的矩阵，那么当x=2的时候就有：
1.当B[1][1]时，i=12,j=1*2所以i取值有1,2,j取值有1,2所以:
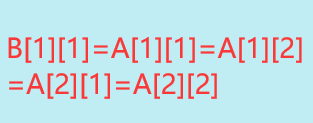
2.当B[1][2]时候i的取值范围为1,2,j的取值范围为3,4所以：
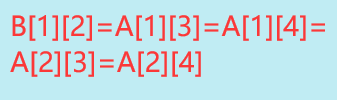
可以发现一个B[][]元素对应一个A中的小矩阵；又因为B中只有0,1这两个值，那么意思就是一个B中元素对应的A中的小矩阵内部的值要么全为0，要么全为1，所以这个问题就可以转化为用前缀和然后分块枚举即可；
时间复杂度为o(n^2);
AC代码：
#include<bits/stdc++.h>
using namespace std;
int n;
string s;
int sum[5205][5205];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>s;
for(int j=0;j<s.length();j++){
if(s[j]<='9'&&s[j]>='0'){
int t=s[j]-'0';
for(int k=j*4+1,y=3;y>=0;k++,y--){
//位移来判断是否为1 这里是顺着来的 就是注意下标
if((t>>y)&1)sum[i][k]=1;
else sum[i][k]=0;
}
}else if(s[j]<='F'&&s[j]>='A'){
int t=s[j]-'A'+10;
for(int k=j*4+1,y=3;y>=0;k++,y--){
if((t>>y)&1)sum[i][k]=1;
else sum[i][k]=0;
}
}
}
}
for(int i=1;i<=n;i++){
//二维前缀和
for(int j=1;j<=n;j++){
sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}
}
int ans=0;
for(int i=n;i>=1;i--){
if(n%i==0){
//整除的原因是由于B[i/x][j/x]，分段的结果 比如：x==2时，那么i就只能取值1,2，j只能取值1,2；如果x==3，那么i取值1,2,3,j取值为1,2,3
int num1=0;
int num2=0;
for(int j=i;j<=n;j+=i){
//遍历每一块的前缀和
for(int k=i;k<=n;k+=i){
if(sum[j][k]-sum[j-i][k]-sum[j][k-i]+sum[j-i][k-i]==0)num1++;
else if(sum[j][k]-sum[j-i][k]-sum[j][k-i]+sum[j-i][k-i]==i*i)num2++;
}
}
int tt=n/i;//一个分为了 这么多块
if(num1+num2==tt*tt){
ans=i;break;
}
}
}
printf("%d\n",ans);
return 0;
}