一文学会解决动态规划问题

动态规划是一种用来解决一类最优化问题的算法思想。简单来说，动态规划将一个复杂的问题分解成若干个子问题，通过综合子问题的最优解来得到原问题的最优解。需要注意的是，动态规划会将每个求解过的子问题的解记录下来，这样当下一次碰到同样的子问题时，就可以直接使用之前记录的结果，而不是重复计算。

一般来说，使用递归或者递推的写法来实现动态规划。其中，递归在此处又称之为记忆化搜索。

1. 动态规划的递归写法

理解动态规划是如何记录子问题的解，来避免下次遇到相同的子问题时的重复计算的

我们以斐波那契数列为例子

斐波那契数列的定义为F(0) = 1，F(1) = 1, F(n) = F(n-1) + F(n-2)(n>=2)

int F(int n){
    if(n == 0 || n == 1) return 1;
    return F(n-1)+F(n-2)
}

在上面这个递归代码中就会涉及很多重复的计算。由于每次都必须从n计算到1，在这个过程中实际的复杂度高达O(2^n)，这个复杂度是非常可怕的

为了避免以上情况，我们可以开一个一维dp数组来记录每次计算的值，如下：

int F(int n){
    if(n == 0 || n == 1) return 1;
    if(dp[n] != -1) return dp[n];
    else{
        dp[n] = F(n-1) + F(n-2);
        return  dp[n];
    }
}

这样就能把计算过的内容记录下来，当下次遇到计算相同的内容时，就可以直接使用了。这个过程就叫记忆化搜索。通过这个过程将复杂度从O(2^n)降到了O(n)

如果一个问题可以被分解为若干个子问题，且这些子问题会重复出现，那么就称这个问题拥有重叠子问题。

2. 动态规划的递推写法

怎么说，总结就是借助一个状态转移方程来实现。我们通过理解一个实例去引出概念：

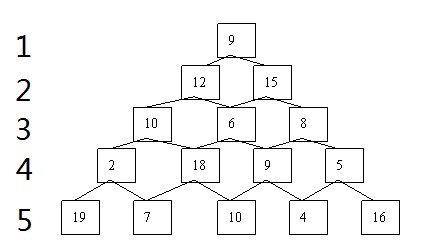
如下图是一个数塔，从顶部出发在每一个节点可以选择向左或者向右走，一直走到底层，要求找出一条路径，使得路径上的数字之和最大.

思路分析：
这道题目如果使用贪婪算法不能保证找到真正的最大和。
在用动态规划考虑数塔问题时可以自顶向下的分析，自底向上的计算。
从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，只要左右两道路径上的最大值求出来了才能作出决策。同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。这样一层一层推下去，直到倒数第二层时就非常明了。
所以第一步对第五层的8个数据，做如下四次决策：
如果经过第四层2，则在第五层的19和7中肯定是19；
如果经过第四层18，则在第五层的7和10中肯定是10；
如果经过第四层9，则在第五层的10和4中肯定是10；
如果经过第四层5，则在第五层的4和16中肯定是16；
经过一次决策，问题降了一阶。5层数塔问题转换成4层数塔问题，如此循环决策…… 最后得到1阶的数塔问题。

算法实现：首先利用一个二维数组data存储数塔的原始数据（其实我们只使用数组data一半的空间，一个下三角矩阵），然后利用一个中间数组dp存储每一次决策过程中的结果（也是一个下三角矩阵）。
初始化dp，将data的最后一层拷贝到dp中。dp[n][j] = data[n][j] (j = 1, 2, …, n) 其中，n为数塔的层数。

dp[1][1] = max(dp[2][1], dp[2][2]) + f[1][1]

在动态规划过程汇总，我们有dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + data[i][j]，最后的结果保存在dp[0][0]中。

#include <bits/stdc++.h>
using namespace std;
int main(){
	int n;
	cin>>n;
	int data[n][n], dp[n][n];
	for(int i = 0; i < n; i++){
		for(int j = 0; j <= i; j++){
			cin>>data[i][j];
		}
	} 
	//1. 初始化边界
	for(int i = 0; i < n; i++){
		dp[n-1][i] = data[n-1][i];
	} 
	//2. 从n-1层开始往上计算dp
	for(int i = n-2; i >= 0; i--){
		for(int j = 0; j <= i; j++){
			//3. 状态转移方程 
			dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + data[i][j];
		}
	} 
	for(int i = 0; i < n; i++){
		for(int j = 0; j <= i; j++){
			cout<<dp[i][j]<<' ';
		}
		cout<<endl;
	}
	return 0;
}

/*
输入：
5
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16

打出dp数组：
59
50 49
38 34 29
21 28 19 21
19 7 10 4 16
*/

如果一个问题的最优解可以由其子问题的最优解有效的构造出来，那么称这个问题拥有最优子结构

总结

一个问题必须拥有重叠子问题和最优子结构，才能使用动态规划解决问题。

以上即是学习动态规划的一点小总结，后续文章会发布很多典型动态规划习题用来巩固这些知识点

01. 最大连续子序列和
02. 最长公共不下降子序列(LIS)
03. 最长公共子序列
04. 最长回文子串
05. 01 背包问题