[SDOI2008]仪仗队
题意:设左下方是坐标 ( 0 , 0 ) (0,0) (0,0),求( 0 , 0 ) 0,0) 0,0)处能够看到的人数。
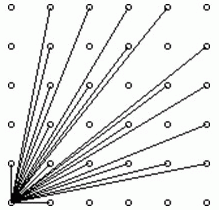
每个人对应一个坐标 ( x , y ) (x,y) (x,y),只要 g c d ( x , y ) = 1 gcd(x, y)=1 gcd(x,y)=1就能被 ( 0 , 0 ) (0,0) (0,0)看到(令 g c d ( 0 , 1 ) = 1 gcd(0,1)=1 gcd(0,1)=1,和 ϕ ( 1 ) = 1 对 应 \phi(1)=1对应 ϕ(1)=1对应)。
欧拉函数
思路:我们只看其中的一半x,另一半和它对称,然后就得到式子 x = ∑ x = 1 n ∑ y = 1 x [ g c d ( x , y ) = 1 ] x=\sum_{x=1}^n\sum_{y=1}^x[gcd(x,y)=1] x=∑x=1n∑y=1x[gcd(x,y)=1]
推式子:
∑ x = 1 n ∑ y = 1 i [ g c d ( x , y ) = 1 ] ∑ x = 1 n ϕ ( x ) \sum_{x=1}^n\sum_{y=1}^i[gcd(x,y)=1]\\ \sum_{x=1}^n\phi(x)\\ x=1∑ny=1∑i[gcd(x,y)=1]x=1∑nϕ(x)
ϕ ( x ) \phi(x) ϕ(x)可以提前用线性筛筛出来,然后再求 ϕ ( x ) \phi(x) ϕ(x)的前n项和x,答案就是2*x+1了(这里的1是 g c d ( 1 , 1 ) = 1 gcd(1,1)=1 gcd(1,1)=1)。
我们是从 x = 1 , y = 1 x=1,y=1 x=1,y=1开始枚举,但看起来 g c d ( 0 , 1 ) 和 g c d ( 1 , 0 ) gcd(0,1)和gcd(1,0) gcd(0,1)和gcd(1,0)并没有算进去,其实x的计算中 ϕ ( 1 ) 其 实 已 经 把 这 些 算 进 去 了 \phi(1)其实已经把这些算进去了 ϕ(1)其实已经把这些算进去了
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e6;
bool st[N];
ll p[N], ou[N], tot;
//欧拉函数的线性筛
void init() {
for(int i=2; i<N; i++) {
if(!st[i]) {
p[tot++] = i;
ou[i] = i-1;
}
for(int j=0; j<tot&&i*p[j]<N; j++) {
st[i*p[j]] = 1;
if(i % p[j] == 0) {
ou[i*p[j]] = ou[i]*p[j];
break;
}
ou[i*p[j]] = ou[i]*(p[j]-1);
}
}
}
int main() {
ou[1] = 1;
init();
ll n, ans = 0;
cin >> n;
//求欧拉函数前n-1项的和
//为啥是n-1,因为是从坐标(0,0)开始计算的。
for(int i=1; i<n; i++) {
ans += ou[i];
}
cout << ans*2+1;
return 0;
}
莫比乌斯反演
推式子:
∑ i = 1 n ∑ j = 1 n [ g c d ( i , j ) = 1 ] ∑ i = 1 n ∑ j = 1 n ∑ d ∣ g c d ( i , j ) μ ( d ) ∑ d = 1 n ∑ i = 1 n ∑ j = 1 n ∑ d ∣ g c d ( i , j ) μ ( d ) ∑ d = 1 n μ ( d ) ∑ i = 1 n d ∑ j = 1 n d 1 ∑ d = 1 n μ ( d ) ⌊ n d ⌋ ⌊ n d ⌋ \sum_{i=1}^{n}\sum_{j=1}^n[gcd(i,j)=1]\\ \sum_{i=1}^n\sum_{j=1}^n\sum_{d|gcd(i,j)}\mu(d)\\ \sum_{d=1}^n\sum_{i=1}^n\sum_{j=1}^n\sum_{d|gcd(i,j)}\mu(d)\\ \sum_{d=1}^n\mu(d)\sum_{i=1}^{\frac nd}\sum_{j=1}^{\frac nd}1\\ \sum_{d=1}^n\mu(d)\lfloor\frac nd\rfloor\lfloor\frac nd\rfloor i=1∑nj=1∑n[gcd(i,j)=1]i=1∑nj=1∑nd∣gcd(i,j)∑μ(d)d=1∑ni=1∑nj=1∑nd∣gcd(i,j)∑μ(d)d=1∑nμ(d)i=1∑dnj=1∑dn1d=1∑nμ(d)⌊dn⌋⌊dn⌋
从上往下解释一下:
第一个式子是总的答案;
第二个式子是莫比乌斯函数的一个性质;
第三个式子加了一个枚举d的操作,这样的话就可以转换成第四个式子;
第四个式子(比较重要)d是i,j的因子所以可以写成 ∑ d ∣ i , d ∣ j \sum_{d|i,d|j} ∑d∣i,d∣j说明d是i,j的因子,同样也说明i,j是d的因子,在区间 [ 1 , n ] [1,n] [1,n]中是d的倍数的有 n d \frac nd dn个。同样也是第五个式子。
然后看到 n d \frac nd dn就可以想到整除分块了。
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e6+10;
ll p[N], sum[N], phi[N], tot, mu[N];
bool st[N];
//线性筛筛出莫比乌斯函数
void init() {
phi[1] = 1, mu[1] = 1;
for(int i=2; i<N; i++) {
if(!st[i]) p[tot++] = i, phi[i] = i-1, mu[i] = -1;
for(int j=0; j<tot&&i*p[j]<N; j++) {
st[i*p[j]] = 1;
if(i % p[j] == 0) {
phi[i*p[j]] = phi[i]*p[j];
mu[i*p[j]] = 0;
break;
}
phi[i*p[j]] = phi[i]*(p[j]-1);
mu[i*p[j]] = -mu[i];
}
}
//对莫比乌斯函数求前缀和
for(int i=1; i<N; i++) {
sum[i] = sum[i-1] + mu[i];
}
}
ll solve(ll n, ll m) {
//整除分块(模板)
ll ans = 0;
if(n > m) swap(n, m);
for(ll i=1, last; i<=n; i=last+1) {
last = min(n/(n/i), m/(m/i));
ans += 1ll*(n/i)*(m/i)*(sum[last]-sum[i-1]);
}
return ans;
}
int main() {
init();
ll n, m;
cin >> n;
cout << solve(n-1, n-1)+2;
return 0;
}