Goffi and GCD
题意:
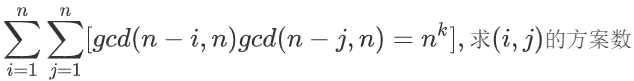
因为 g c d ( n − i , n ) , g c d ( n − j , n ) gcd(n-i,n),gcd(n-j,n) gcd(n−i,n),gcd(n−j,n)都是n的因子(且不为n)所以乘起来不会超过 n 2 n^2 n2所以等价于求
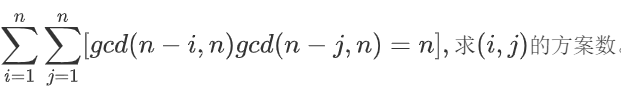
推式子
∑ i = 1 n ∑ j = 1 n [ g c d ( n − i , n ) g c d ( n − j , n ) = n ] ∑ i = 1 n ∑ j = 1 n ∑ x ∣ n ∑ y ∣ n [ x y = n ] [ g c d ( n − i , n ) = x ] [ g c d ( n − j , n ) = y ] ∑ x ∣ n ∑ y ∣ n [ x y = n ] ∑ i = 1 n [ g c d ( i , n ) = x ] ∑ j = 1 n [ g c d ( j , n ) = x ] ∑ x ∣ n ∑ y ∣ n [ x y = n ] ϕ ( n x ) ϕ ( n y ) ∑ x ∣ n ϕ ( n x ) ϕ ( x ) \sum_{i=1}^n\sum_{j=1}^{n}[gcd(n-i,n)gcd(n-j,n)=n]\\ \sum_{i=1}^n\sum_{j=1}^n\sum_{x|n}\sum_{y|n}[xy=n][gcd(n-i,n)=x][gcd(n-j,n)=y]\\ \sum_{x|n}\sum_{y|n}[xy=n]\sum_{i=1}^n[gcd(i,n)=x]\sum_{j=1}^n[gcd(j,n)=x]\\ \sum_{x|n}\sum_{y|n}[xy=n]\phi(\frac nx)\phi(\frac ny)\\ \sum_{x|n}\phi(\frac nx)\phi(x)\\ i=1∑nj=1∑n[gcd(n−i,n)gcd(n−j,n)=n]i=1∑nj=1∑nx∣n∑y∣n∑[xy=n][gcd(n−i,n)=x][gcd(n−j,n)=y]x∣n∑y∣n∑[xy=n]i=1∑n[gcd(i,n)=x]j=1∑n[gcd(j,n)=x]x∣n∑y∣n∑[xy=n]ϕ(xn)ϕ(yn)x∣n∑ϕ(xn)ϕ(x)
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
ll eular(ll x) {
//利用欧拉函数的性质求phi(x)
ll ans = x;
for(ll i=2; i*i<=x; i++) {
if(x % i == 0) {
ans = ans/i*(i-1);
while(x % i == 0) x /= i;
}
}
if(x > 1) ans = ans/x*(x-1);
return ans;
}
int main() {
ll n, m;
while(scanf("%lld %lld", &n, &m) != EOF) {
ll ans = 0;
if(m == 2 || n == 1) ans = 1;
else if(m == 1){
for(ll i=1; i*i<=n; i++) {
if(n % i == 0) {
if(n/i != i) ans = (ans+eular(i)*eular(n/i)*2%mod)%mod;
else ans = (ans+eular(i)*eular(i)%mod)%mod;
}
}
}
printf("%lld\n", ans);
}
return 0;
}