Codeforces Round #641 (Div. 2)ABCD题解

其他 2021-01-24 22:09:50 阅读次数: 0

A题：Orac and Factors 链接传送门
水题 分类讨论a是奇数/偶数 操作就行了 奇数的话对a求因子 算贡献 代码如下

ll a[manx];

 
 
int main()
{
    
    
 
    ll t=read();
    while(t--)
    {
    
    
        ll a,b;
        a=read();
        b=read();
 
        if(a&1)
        {
    
    
            for(int i=2; i<=a; i++)
                if(a%i==0)
                {
    
    
                    a+=i;
                    b--;
                    break;
                }
        }
        a+=b*2;
        cout<<a<<endl;
    }
    return 0;
}

B题 Orac and Models
题意：给你n个数 分别是s[i] 要你选一些出来 满足下标递增 而且对应的值是成倍数变化的 在这里插入图片描述
样例1 3 6 --》2的贡献
~~ 2 1 2 4 / 1 3 9 -->3的贡献 dp一下就OK了

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
inline ll read()
{
    
    
    char c=getchar();
    ll f=1,x=0;
    while(c<'0'||c>'9')
    {
    
    
        if(c=='-')
            f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
    
    
        x=(x<<1)+(x<<3)+(c^'0');
        c=getchar();
    }
    return x*f;
}
ll gcd(ll a,ll b)
{
    
    
    return b==0?a:gcd(b,a%b);   //最大公因数
}
ll lcm(ll a,ll b)
{
    
    
    return a/__gcd(a,b)*b;
}
ll qp(ll a,ll b, ll p)
{
    
    
    ll ans = 1;    //逆元   (分子*qp(分母,mod-2,mod))%mod;
    a%=p;
    while(b)
    {
    
    
        if(b&1)
        {
    
    
            ans = (ans*a)%p;
            --b;
        }
        a =(a*a)%p;
        b >>= 1;
    }
    return ans%p;
}
long long mode(long long a,long long b,long long mod)
{
    
    
    long long ans=1;
    if(b==0)
    {
    
    
        return ans%mod;
    }
    while(b)
    {
    
    
        if(b%2==1)
        {
    
    
            b--;
            ans=ans*a%mod;
        }
        a=a*a%mod;
        b=b/2;
    }
    return ans;
}//快速幂%
/*最小公倍数lcm(a,b)=a*b/gcd(a,b);
gcd(ka,kb)=k*gcd(a,b);
gcd(s/a,s/b)=s/gcd(a,b);
gcd(x^a-1,x^b-1)=x^gcd(a,b)-1;
gcd(f[a],f[b])=f[gcd(a,b)];
lcm(ka,kb)=k*lcm(a,b);
lcm(f[a],f[b])=f[lcm(a.b)];*/
/*
void prime(ll n){
vector<ll>v;//用的时候记得拿出去
ll tmp = n;
if(n % 2 == 0) {
v.push_back(2);
while (n % 2 == 0) {
n /= 2;
}}for(ll i = 3; i * i <= tmp; i += 2){
if(n % i == 0) {
v.push_back(i);
}
while(n % i == 0){
n /= i;
}}if(n > 2)
v.push_back(n);
}*/

const int manx=1e6+5;
ll a[manx];
ll dp[manx];
vector<ll>v[manx];
void op(){
    
    


for(int i=1;i<=100000;i++){
    
    
        for(int j=i*2;j<=100000;j+=i)
            v[j].pb(i);
    }
}
int main(){
    
    
       op();
    ll t=read();
    while(t--){
    
    
        ll n=read(),ans=1;
    for(int i=1;i<=n;i++) {
    
    a[i]=read();
    dp[i]=1;}
        for(int i=1;i<=n;i++){
    
    
            for(auto j: v[i]) if(a[j]<a[i]) dp[i]=max(dp[i],dp[j]+1);
            ans=max(ans,dp[i]);
        }
     printf("%lld\n",ans);
    }
    return 0;
}

（这个题莫名其妙WA1了，交了接近20分钟才发现）QAQ

C题 数论 Orac and LCM
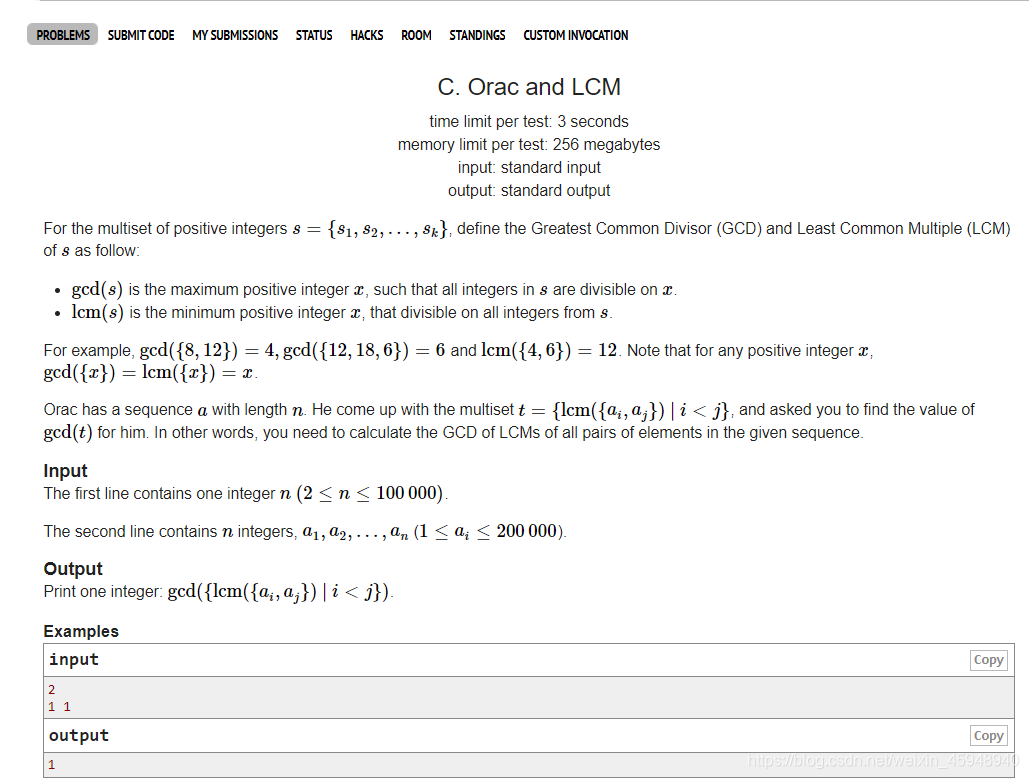
在这里插入图片描述
我个人而言，用的方法是先预处理一个素数表prime 然后对对每个a[i]质因子分解 并且存入vector中 即对应质因子 prime[i] ->幂次
然后计算ans时判断每个质因子的容器大小是否大于等于 n - 1如果是则说明数组中少于两个数没有这个质因子，则答案必定要乘上这个质因子然后我们对容器sort一下 如果容器的大小等于 n 则取第二个元素即次小幂次，如果等于 n- 1则取第一个元素即最小幂次，以此来计算该因子的贡献 （不开ll见祖宗）
GCD LCM按幂次 的食用方法链接

    • 队友反应我写的题解看不懂 。
      -先看看上面的链接吧
      两两lcm 取的是质因子幂次最大 那么假设该因子 n个数都有 那么一定存在一组 即最小幂次和次小幂次的组合取max 所以 次小幂次被保留了
      进入gcd 环节 同理 一定有一组是 与之前的次小幂次组合的 取min那么保留的就是次小幂次
#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
inline ll read()
{
    
    
    char c=getchar();
    ll f=1,x=0;
    while(c<'0'||c>'9')
    {
    
    
        if(c=='-')
            f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
    
    
        x=(x<<1)+(x<<3)+(c^'0');
        c=getchar();
    }
    return x*f;
}
ll gcd(ll a,ll b)
{
    
    
    return b==0?a:gcd(b,a%b);   //最大公因数
}
ll lcm(ll a,ll b)
{
    
    
    return a/__gcd(a,b)*b;
}
ll qp(ll a,ll b, ll p)
{
    
    
    ll ans = 1;    //逆元   (分子*qp(分母,mod-2,mod))%mod;
    a%=p;
    while(b)
    {
    
    
        if(b&1)
        {
    
    
            ans = (ans*a)%p;
            --b;
        }
        a =(a*a)%p;
        b >>= 1;
    }
    return ans%p;
}
long long mode(long long a,long long b,long long mod)
{
    
    
    long long ans=1;
    if(b==0)
    {
    
    
        return ans%mod;
    }
    while(b)
    {
    
    
        if(b%2==1)
        {
    
    
            b--;
            ans=ans*a%mod;
        }
        a=a*a%mod;
        b=b/2;
    }
    return ans;
}//快速幂%
/*最小公倍数lcm(a,b)=a*b/gcd(a,b);
gcd(ka,kb)=k*gcd(a,b);
gcd(s/a,s/b)=s/gcd(a,b);
gcd(x^a-1,x^b-1)=x^gcd(a,b)-1;
gcd(f[a],f[b])=f[gcd(a,b)];
lcm(ka,kb)=k*lcm(a,b);
lcm(f[a],f[b])=f[lcm(a.b)];*/
const int manx=1e6+7;
ll vis[manx],prime[manx];
vector<ll>v[manx];
ll cnt=0,ans=1;
void init(){
    
    
  for(int i=2;i<=200005;i++){
    
    
        if(!vis[i]) prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<=200005;j++){
    
    
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}
void check(ll x){
    
    
  for(int j=1;j<=cnt;j++){
    
    
            if(prime[j]*prime[j]>x) break;
            ll xx=0;
            if(x%prime[j]==0){
    
    
                while(x%prime[j]==0) x/=prime[j],xx++;
                v[prime[j]].pb(xx);
            }
        }
        if(x>1) v[x].pb(1);
}
int main(){
    
    
    init();
    ll n;
    cin>>n;
    vis[1]=1;
    for(int i=1;i<=n;i++){
    
    
        ll x;
        cin>>x;
        check(x);
    }
    for(int i=1;i<=cnt;i++){
    
    
        int x=prime[i];
        sort(v[x].begin(),v[x].end());
        ll m=v[x].size();
        ll ma=0;
        if(m==n) ma=v[x][1];
        else if(m+1==n) ma=v[x][0];
        for(int j=1;j<=ma;j++) ans*=x;
    }
    cout<<ans;
    return 0;
}

有个大佬（唐少爷）教了我另一种写法 巨短 也巨强

对于a1 ,产生的Icm为lcm(a1 , a2), lcm(a1 , a3) … lcm(a1 , an)
产生的gcd_ 1为gcd ( lcm(a1 , a2), lcm(a1 , a3) … lcm(a1 , an) )
因为参与gcd. 1的每-项都是a1的倍数
所以gcd( lcm(a1 , a2) , lcm(a1 , a3) … lcm(a1 , an) )可以化为lcm(a1 , gcd (a2, a3,… an) )
那么最后答案就为ans = gcd(gcd 1 , gcd_ 2…gcd_ n)，我们维护-一个后缀

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 3e5 + 10;
int gcd(int a , int b)
{
    
    
    return b ? gcd(b , a % b) : a;
}
int lcm(int a , int b)
{
    
    
    return a * b / gcd(a , b);
}
int a[N] , suf[N];
signed main()
{
    
    
    ios::sync_with_stdio(false); 
    int n , ans = 0;
    cin >> n; 
    for(int i = 1 ; i <= n ; i ++) cin >> a[i];
    for(int i = n ; i >= 1 ; i --) suf[i] = gcd(suf[i + 1] , a[i]);
    for(int i = 1 ; i <= n ; i ++) ans = gcd(ans , lcm(a[i] , suf[i + 1]));
    cout << ans << '\n' ; 
    return 0;
}

D题大水题 我个人认为跟AB一个档次 ，运气好D只是个思维题。
Orac and Medians 传送门
题意就是给你n个数 然后对于任意[l,r]区间 长度为s 则可以把这个区间全部的数变成 (s+1)/2小的数 问你能不能把整个区间变成k 那么我们有一种策略 如下我就直接放图了 跟队友讲了遍
在这里插入图片描述
假设一个区间有除了k以外的数 那么如果存在 a[i]>=k而且a[i+1]>=k||a[i+2]>=k 我们一定能yes 为什么呢 ？ 首先 保证区间中有k这个数 否则一定no 然后我们看策略 如果a[i] a[i+1]满足条件 那么一定可以使得他左边或者右边一直扩展为>=k的数 直到扩展到值为k的数时 此时与k相邻的数是>=k的 那么根据题意 (2+1)/2 不论如何都是把这个区间同化为了k
以此类推 逐步同化 a[i] a[i+2]也是同理 他一定可以使得[i,i+2] 变为>=k的数 因为 (3+1)/2=2 就算a[i+1]是这区间最小的 也不会由他变

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
inline ll read()
{
    
    
    char c=getchar();
    ll f=1,x=0;
    while(c<'0'||c>'9')
    {
    
    
        if(c=='-')
            f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
    
    
        x=(x<<1)+(x<<3)+(c^'0');
        c=getchar();
    }
    return x*f;
}
ll gcd(ll a,ll b)
{
    
    
    return b==0?a:gcd(b,a%b);   //最大公因数
}
ll lcm(ll a,ll b)
{
    
    
    return a/__gcd(a,b)*b;
}
ll qp(ll a,ll b, ll p)
{
    
    
    ll ans = 1;    //逆元   (分子*qp(分母,mod-2,mod))%mod;
    a%=p;
    while(b)
    {
    
    
        if(b&1)
        {
    
    
            ans = (ans*a)%p;
            --b;
        }
        a =(a*a)%p;
        b >>= 1;
    }
    return ans%p;
}
long long mode(long long a,long long b,long long mod)
{
    
    
    long long ans=1;
    if(b==0)
    {
    
    
        return ans%mod;
    }
    while(b)
    {
    
    
        if(b%2==1)
        {
    
    
            b--;
            ans=ans*a%mod;
        }
        a=a*a%mod;
        b=b/2;
    }
    return ans;
}//快速幂%
/*最小公倍数lcm(a,b)=a*b/gcd(a,b);
gcd(ka,kb)=k*gcd(a,b);
gcd(s/a,s/b)=s/gcd(a,b);
gcd(x^a-1,x^b-1)=x^gcd(a,b)-1;
gcd(f[a],f[b])=f[gcd(a,b)];
lcm(ka,kb)=k*lcm(a,b);
lcm(f[a],f[b])=f[lcm(a.b)];*/
 
const int maxn=1e6+7;
ll a[maxn];
int main()
{
    
    
 
	ll t=read();
 
	while(t --)
	{
    
    
		ll n=read();
		ll k=read();
		ll flag = 1,cnt = 0;
 
		    for(int i=1;i<=n;i++){
    
    
		   a[i]=read();
			if(a[i]!=k) flag = 0;
			else{
    
     
			cnt ++;
			}
		}
		if(!cnt)
		{
    
    
			printf("no\n");
			continue;
		}
		   for(int i=1;i<=n-1;i++){
    
    
			if(a[i] >= k)
			{
    
    
				if(a[i + 1] >= k ||( a[i + 2] >= k&& i <= n - 2))
				{
    
    
					flag = 1;
					break;
				}
			}
 
	}
	if(flag) {
    
    printf("yes\n");}
		else {
    
    printf("no\n");}
	}
	return 0;
}

在这里插入图片描述
推荐一个朋友捣鼓出来的字符串题 传送门
n个字符串选3个问能不能组成目标串 目标串 字符串 长度<50 n 1e5
// —— // 我个人在想如果3扩展为k 长度扩大 这又该怎么写

猜你喜欢

转载自blog.csdn.net/weixin_45948940/article/details/106092269
今日推荐
国产云输入法——仅华为无云端数据上传安全问题
开源日报 | 工业开源项目OGG 1.0；姐姐，你要和我一起配置火狐吗；苹果AI遥遥落后？Fedora 40
开放签电子签章：停止新增，优化体验，前进更进（五一假期前工作）
开源日报 | 中学生开源前端动画引擎；全球首个Llama3 8B中文版开源模型；联想电脑恐出局；Linus讽刺AI炒作
“百模大战”必有一战 | 2024中国“百模大战”竞争格局分析
最强开源大模型 Llama 3 上架 Gitee AI
周排行
自媒体文章如何提高原创度以及如何检测原创度
开启qq邮箱的smtp服务
Qt程序单次启动（QSingleApplication类）
国外的外包网站
更新IDEA主题——放飞代码风格
cocos2dx 实现搓牌效果（翻牌效果），包括铺平动画
dict和json之间的互相转换
angular的一些思考
. Fibonacci数列是这样定义的： F[0] = 0 F[1] = 1 for each i ≥ 2: F[i] = F[i-1] + F[i-2] 因此，Fibonacci数列就形如：0, 1
洛谷P1064 金明的预算方案
每日归档
更多
2024-04-25(22)
2024-04-24(36)
2024-04-23(26)
2024-04-22(39)
2024-04-21(0)
2024-04-20(6)
2024-04-19(5)
2024-04-18(0)
2024-04-17(5)
2024-04-16(70)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022