HMM原理2：decoding问题解法（维特比算法，近似算法）

1. 维特比算法

1.1 前提概要

我们知道HMM需要解决三个问题，其中的decoding问题需要用维特比算法，那么什么是维特比呢？维特比算法是一种动态规划算法，在学xgboost的时候我们使用了一个技巧，t+1时刻的预测值为t时刻的预测值加上t+1时刻的预测值。维特比有点相似。

先来回顾下，维特比解决的什么问题，已知观测序列和参数，求隐藏序列。注意重点是求隐藏序列，所以问题的本质是找到隐藏序列。
举个例子：盒子和球模型（来自小蓝书），已知如下：

我们知道观测序列为{红，白}，求的是隐藏序列（来自哪个盒子），可能的结果为{1,1}、{1,2}、{1,3}、{2,1}、{2,2}、{2,3}、{3,1}、{3,2}、{3,3}，问题的本质是求这9种可能哪个概率最大，概率最大的那个就是我们的答案。将所有可能的结果呈现在二维图中：

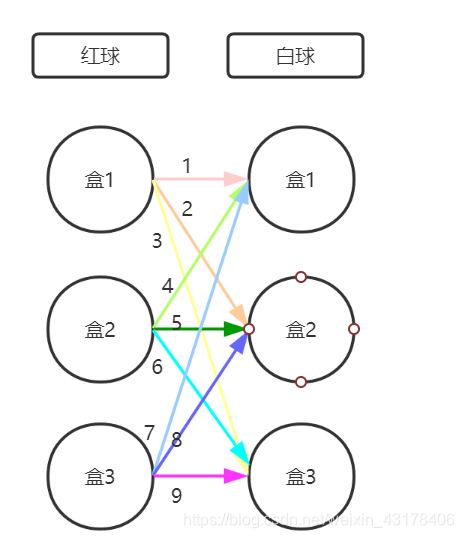
对上图进行阐释：在已知第一次为红色时，可以选择第1、第2、第3个盒子；第二次为白色亦同。由此从第一次红色到第二次白色就有9条路径可以选择。
假如第一次和第二次结果对应的盒子分别是盒子1和盒子2，也就是说选择了路径2。那么我们如果确保图中的路径2概率最大呢？
从第二次结果考虑，只要从开始到第一次结果选择的路径正确，且从第一次结果到第二次结果的转移正确（即第二次正确选择了盒子2），就能保证我们整个路径正确。
广泛地讲：只要从开始到第t次结果选择的路径是正确的，且第t+1时刻正确选择（t时刻到t+1时刻转移正确）就能保证直到t+1时刻我们的选择都是对的，得到的答案就是最优答案。此外t时刻的结果又和t-1时刻的正确路径有关，因此可以一直向前推，就是维特比算法的思想。
还是以上图中的小蓝书为例。直接通过例子感受维特比算法的过程。

1.2 实例计算1

我们从最终的t=2时刻开始看

• t=2时刻的概率记做${\delta }_2$依赖于三部分:
  • 一：t=1时刻的概率${\delta }_1$
  • 二：t=1时刻从状态j转移到状态i的概率，即转移矩阵中的$a_{ji}$
  • 三：t=2时刻状态为i（盒子为i），观测$o_2$为白的概率，其实就是B中的$b_i(k=o_2)$，即发射矩阵中的$b_i(o_2)$
• t=1时刻的概率记做${\delta }_1$依赖于三部分:
  • 一：t=0时刻的概率${\delta }_0=1$
  • 二：t=0时刻从状态j（对于t=0时刻，只有状态0）转移到状态i的概率，即π中的${\pi }_i$
  • 三：t=1时刻状态为i（盒子为i），观测$o_1$为红的概率，其实就是B中的$b_i(k=o_1)$，即发射矩阵中的$b_i(o_2)$

上述介绍了计算的组成部分，或者说大致思想，但是具体怎么算呢，下面将会仔细讲解。

• t=2时：
  • 一：${\delta }_1$，该值是什么，我们先放下，继续看第二、第三部分
  • 二：t=1时刻从隐藏状态j转移到隐藏状态i的概率，我们知道t=1时刻的隐藏状态j有三种（j为盒子1，盒子2，盒子3），同时t=2时的隐藏状态i（i为盒子1，盒子2，盒子3）有三种情况，也就是说第二部分可以计算出九个取值
  • 三：t=2时刻状态为i（盒子为i），观测$o_2$为白的概率，其实就是B中的$b_i(k=o_2)$，即发射矩阵中的$b_i(o_2)$，i有三种情况，故有三个取值
  • 二有9种取值，三有三种取值，因此我们可以根据三中的i将二也分成三大类（每个大类包含三个小类）
  • 综上，我们可以得到${\delta }_2(i)={\delta }_1(j)a_{j1}{b}_1(o_2),i=1,2,3;j=1,2,3$。具体来讲，得到的三个取值为$${\delta }_2(1)={\delta }_1(j)a_{j1}{b}_1(o_2),j=1,2,3$$$${\delta }_2(2)={\delta }_1(j)a_{j2}{b}_1(o_2),j=1,2,3$$$${\delta }_2(3)={\delta }_1(j)a_{j3}{b}_1(o_2),j=1,2,3$$
  • 对于t=2时刻，隐藏状态就是${\delta }_2(1),{\delta }_2(2),{\delta }_2(3)$三个数中最大那个数对应的隐藏状态，记做$i_2^{\ast }$（最终的隐藏序列$I^{\ast }=(i_1^{\ast },i_2^{\ast })$），（ps：对于t=2时刻，选择哪个隐藏状态呢，那就分别计算三种隐藏状态的概率吧，选择概率最大的那个）假如\delta_2(3)最大，那么第二步的隐藏状态就是3，然而还有一个问题，因为j有三种取值，故\delta_2(3)也有三种取值，那么\delta_2(3)到底是什么呢？其实也是这三种结果中的最大的那个。
  • 综上所述，可以得到两个结论，$$i_2^{\ast }=arg\underset{1\le i\le 3}{\max }({\delta }_2(i))公式1$$$${\delta }_2(i)=\underset{1\le j\le 3}{\max }{\delta }_1(j)a_{ji}{b}_i(o_2)公式2$$对于其他时刻，公式2依旧成立，公式1只有在最后一个时刻才用得到。不过也看到一个事实，t=2时刻的结果不能立马算出来，因为他还取决于t=1时刻，因此，计算时，我们要先从t=1时刻开始算。下面就讲如何计算

1.3 实例计算2

上文中小蓝书A，B，π不变，但是观测序列变为{红，白，红}，计算过程如下：

1.4 公式总结

第2章和第3章我们使用了实例讲解维特比算法的求解过程，现在将上述过程总结为公式。

• 输入：模型$\lambda =(A,B,\pi )$和观测$O=(o_1,o_2,...,o_T)$
• 输出：最优路径$I^{\ast }=(i_1^{\ast },i_2^{\ast },...i_T^{\ast })$

1. 初始化：$$\delta (i)={\pi }_i{b}_i(o_i)$$$$\psi (i)=0$$
2. 递推，对于t=2,3，…T$${\delta }_t(i)=\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}]b_i(o_t)，其中N指隐藏状态的个数$$$${\psi }_t(i)=arg\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}]$$
3. 终止$$P^{\ast }=\underset{1\le i\le N}{\max }{\delta }_T(i)$$$$i_T^{\ast }=arg\underset{1\le i\le N}{\max }{\delta }_T(i)$$
4. 最终路径回溯对于t=T-1，T-2,…1$$i_t^{\ast }={\psi }_{t+1}(i_{t+1}^{\ast })$$求得最优路径$I^{\ast }=(i_1^{\ast },i_2^{\ast },...i_T^{\ast })$

ps：由于例子中没有提到$\psi (i)$,先说明一下：${\psi }_t(i)=arg\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}]$其实就是t时刻，隐态为i时，t-1时刻选择的隐藏状态，很有可能就是最终的$i_{t-1}^{\ast }$，为什么是很有可能，因为t时刻，隐态为i时，${\delta }_t(i)$不一定是最大的。

1.5 ps

ps：上述文字部分在表述上可能有所问题，但是是为了理解，其中图片的计算部分，以及第4章公式总结部分是正确的

2. 近似算法

理解了维特比算法，再来看近似算法的公式，可能就比较容易理解了，再此不再展开来讲，附上小蓝书关于近似算法的描述：

其中$\alpha 和\beta$是前后向算法中引入的变量，具体可见HMM原理3：前后向算法