Hash表
哈希表 :
- 存储结构
- 开放寻址法
- 拉链法
- 字符串哈希方式
作用 : 把一个比较庞大的空间/值域 或者 一个比较的复杂的数据结构 映射到 一个比较小的空间 0 ~ N ( 10^5 – 10^6 )
ex : 0 ~ 10^9 -> 0 ~ 10^5
离散化 : 一种特殊的哈希方式 需要数列保序才能进行操作
例题 :
// 模拟散列表 :
// 维护一个集合 , 支持如下操作 :
// 1. I x 插入一个数 x
// 2. Q x 询问 x 是否在集合中出现过
// 操作个数 10^5 每个数的范围 -1e9 ~ 1e9
// 做法 : 通过一个哈希函数 将输入的 x 映射到 一个较小的值域范围
// h ( x ) -> 0 ~ 10^5 h( x ) 被称为哈希函数
hash函数的做法 :
- x mod 10^5 -> 0 ~ 10^5 [^一般来说 , mod的这个数要取质数 , 而且这个质数要离2的整次幂尽可能的远]
- 冲突 – 可能会把若干不同的数映射到同一个数 ex : h( 10 ) = 2 , h( 5 ) = 2 ;
除留余数法用的较多
H(key)=key MOD p (p<=m m为表长)
很明显,如何选取p是个关键问题。使用举例
比如我们存储3 6 9,那么p就不能取3
因为 3 MOD 3 == 6 MOD 3 == 9 MOD 3
p应为不大于m的质数或是不含20以下的质因子的合数,这样可以减少地址的重复(冲突)比如key = 7,39,18,24,33,21时取表长m为9 p为7 那么存储如下
取质数的技巧: 取题目所给最大范围的第一个质数
#include <iostream>
using namespace std;
const int N = 100010 ;
int main()
{
for(int i = 100000; ; i ++ )
{
bool flag = true ;
for(int j = 2 ; j * j <= i; j ++ )
{
cout << "j = " << j << endl ;
if(i % j == 0)
{
flag = false ; break ;
}
}
if(flag)
{
cout << i << endl ;
break ;
}
}
return 0 ;
}
处理冲突的方式 :
拉链法 :
开一个一维数组来存储所有的哈希值 哈希算法是一种期望算法 , 平均情况下 , 每条链的长度可以看作是一个常数 , 在一般情况下哈希表的复杂度可以看成 O( 1 ) , 在一般情况下 , 哈希表不需要进行删除 元素的操作 , 一般只有 添加和查找 两种操作 , 添加一个数 x , 先求 h( x ) 看其对应在数组上哪个位置 , 在把其放到对应下标的链(单链表)上 , 删除操作 : 一般来说不会直接把元素从链表中删去, 而是开一个bool数组/变量 , 给要删除的元素打上标记 .
拉链法
拉链法也称开散列法(open hashing)。
拉链法是在每个存放数据的地方开一个链表,如果有多个 key 索引到同一个地方,只用把他们都放到那个位置的链表里就行了。查询的时候需要把对应位置的链表整个扫一遍,对其中的每个数据比较其 key 与查询的 key 是否一致。如果索引的范围是 1~M,哈希表的大小为 N,那么一次插入/查询需要进行期望 O(N / M) 次比较。
如下图所示 :
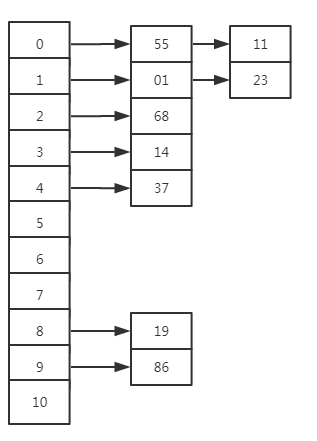
bool 函数返回的默认值是 true , bool 变量的默认值是 false
模版代码 :
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100003 ;
int h[N] , e[N] , ne[N] , idx ;
void insert(int x)
{
// 计算哈希值
int k = (x % N + N) % N ; // 这里 + N 再模 N 是防止x为负数的情况
e[idx] = x ; ne[idx] = h[k] ; h[k] = idx ++ ;
}
bool find(int x)
{
int k = (x % N + N) % N ;
for(int i = h[k] ; i != -1; i = ne[i])
{
if(e[i] == x) return true ;
}
return false ;
}
int main()
{
int n ; scanf("%d",&n) ;
memset(h,-1,sizeof h) ;
while (n -- )
{
char op[2] ; int x ; scanf("%s",op) ;
if(*op == 'I') {
scanf("%d",&x) ; insert(x) ; }
else
{
scanf("%d",&x) ;
if(find(x)) puts("Yes") ;
else puts("No") ;
}
}
return 0 ;
}
开放寻址法 :
只开了一个一维数组 , 没有开单链表 , 但这种做法开的数组一般要开到题目数据范围的 2 ~ 3 倍 , ex : 题目给定范围 是 1e5 那么数组长度要开到 2e5 ~ 3e5
又称闭散列法 :
闭散列方法把所有记录直接存储在散列表中,如果发生冲突则根据某种方式继续进行探查。
比如线性探查法:如果在 d 处发生冲突,就依次检查 d + 1 , d+2 ……
删除操作 :
首先开散列法是可以直接删除元素的,但是闭散列法是不行的,拿前面的双探测再散列来说,假如我们删除了元素1,将其位置置空,那 23就永远找不到了。正确做法应该是删除之后置入一个原来不存在的数据,比如-1 . 但一般我们不会直接删除 , 而是创建bool数组,然后对要删除的元素进行标记即可.
类比上厕所
模版代码 :
// 开放寻址法
#include <iostream>
#include <cstring>
using namespace std;
// 开放寻址法中的数组 一般要开到题目所给数据范围的 2 ~ 3 倍
const int N = 200003 , null = 0x3f3f3f3f;
int h[N] ;
int find(int x)
{
int t = (x % N + N) % N ;
while (h[t] != null && h[t] != x)
{
t ++ ;
if(t == N) t = 0 ;
}
return t ;
}
int main()
{
int n ;
scanf("%d",&n) ;
memset(h,0x3f,sizeof h) ;
while(n --)
{
char op[2] ; int x ; scanf("%s%d",op,&x) ;
int k = find(x) ;
if(*op == 'I') h[k] = x ;
else
{
if(h[k] != null) puts("Yes") ;
else puts("No") ;
}
}
return 0 ;
}
memset是按字节来重置 , 每次一个字节 , 整型数据占4个字节 , 每个字节是0x3f, 一共四个字节, 就是0x3f3f3f3f 一个字节 8 位
memset 不能处理 vector
字符串哈希方式 :
字符串前缀哈希法 :
ex :
str = “ABCABCDEHELLOWORLD”
h[0] = 0
h[1] = "A"的hash值
h[2] = "AB"的hash值
h[3] = "ABC"的hash值
h[4] = "ABCA"的hash值
哈希值处理方法 :
把字符串看成是一个 p 进制的数 – 把字符串转化成数字
注意, : 字符串可能很长, 就会导致转换后的p进制的数很大 , 这样得到的数字不好存储, 在这里我们一般将其进行 取模 处理 , 即将其 % Q ( Q为一个很大的数 , 一般取2^64 )
注意:
不能映射成 0 ( 一般选择 从一 开始 , 或者直接用 ASCII 码)
原因 : 假设 将 A 映射到 0 , A的p进制数 就是 0 , “AA” 为 00 , 也等于 0 ; 这样只要是A的重复字符串转换后得到的数都相等 -> 0 ;
字符串哈希与数字哈希不一样 , 假定 rp 足够好 , 完全不考虑冲突的情况
经验值 : p = 131 或者 13331 Q取 2^64 ;
这样处理的好处 : 可以利用前缀哈希 计算出 任意一个子串的哈希值
h[L,R] = h[R] - h[L - 1] * p^(R - L + 1) ;
EX : ( “ABCD” )10(十进制) A = 1 , B = 2 , C = 3 , D = 4 ;
求BC的哈希值 , h[2,3] = h[3] - h[2 - 1]*10^(3 - 2 + 1) = 123 - 100 = 23 ;
如果不能理解公式这么来的 , 可以这么考虑 ;
因为我们在字符串哈希中把每个前缀字符串看成一个p进制数, 如果我们要求某一段子串的哈希值 , 可以通过其前缀字符串减掉其前面的字符串的方式 : 如下 :
EX : ( “ABCD” )10(十进制) A = 1 , B = 2 , C = 3 , D = 4 ; 求 "CD"的哈希值
h[4] = 1234 , h[2] = 12 ; 这时子串的哈希值就等于 其前缀字符串的哈希值减去其前面的前缀字符串的哈希值 , 就等于 1234 去掉 12 --> 34 , 但是因为这两个字符串不在同一位上 , 所以需要把 12 * 10 ^ (4 - 3 + 1) 进位 才能使得 成功去掉前面两位的数字 , 最终得到的结果即是我们要求的子串的哈希值 .
注意 : 前面我们提到 Q 需要取模一个 2^64 , 这里有个技巧 ,我们可以用 unsigned long long 来存储所有的 h , 这时不需要取模 , 因为其会溢出 , 而其溢出就相当于取模( 因为其数据范围为2^64 ) , 等价于 % 2^64 , 这样处理后求子串的哈希值的时间复杂度为 O( 1 )
预处理前缀字符串的哈希值 : h[i] = h[i - 1] * p + str[i] ;
代码如下 :
// 给定一个长度为n的字符串 , 再给定 m 个询问 , 每个询问包含四个整数
// l1 , r1, l2, r2 判断 [l1,r1] 和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同
#include <iostream>
using namespace std;
// 利用 ULL 溢出等于取模的特性 , 省去了求哈希值时的取模操作
typedef unsigned long long ULL ;
const int N = 100010 , P = 131 ;
int n , m ;
ULL h[N] , p[N] ; char str[N] ;
ULL get(int l,int r)
{
return h[r] - h[l - 1]*p[r - l + 1] ;
}
int main()
{
scanf("%d%d%s",&n,&m,str) ;
p[0] = 1 ;
// 预处理前缀字符串的哈希值 和 p数组
for(int i = 1;i <= n;i ++ )
{
p[i] = p[i-1] * P ;
h[i] = h[i - 1] * P + str[i - 1] ;
// 注意 : 因为输入字符串的时候其下标是从 0 开始的 , 所以这里赋值的时候要从 i - 1 开始 .
// 也可以通过 在输入的时候 str + 1 的方式 ,使其从下标为 1 的位置开始赋值 ,
}
// 处理询问
while (m --)
{
int l1 , r1 , l2 , r2 ;
scanf("%d%d%d%d",&l1,&r1,&l2,&r2) ;
if(get(l1,r1) == get(l2,r2)) puts("Yes") ;
else puts("No") ;
}
return 0 ;
}
STL使用技巧
vector 变长数组 , 倍增的思想
- size( ) 返回元素的个数
- empty( ) 返回是否为空
- clear( ) 清空 [^队列无清空函数]
pair<int,int> 存储一个二元组
string . 字符串 substr( ) c_str( )
queue 队列 , push( ) front( ) pop( )
priority_queue 优先队列 . push( ) top( ) pop( )
stack 栈 push( ) top( ) pop( )
deque 双端队列
set . map . multiset .multimap 基于平衡二叉树 ( 红黑树 ) , 动态维护有序序列
unordered_set , unordered_map , unordered_multiset , unordered_multimap 哈希表
bitset 压位
// 不需要记忆所有容器的操作函数
// 有些不常用的函数 直接当我们使用的时候去查找其用法即可
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>
using namespace std;
int main()
{
vector<int> a(10) ; // 定义一个长度为10的vector
vector<int> a(10,3) ; // 定义一个长度为10的vector并且将所有元素的值赋为3
a.size() ; a.empty() ; // 所有容器共有 时间复杂度为O( 1 )
a.clear() ; // 清空 队列无这个函数
a.front() , a.back() , a.push_back() , a.pop_back() ; // 取a的第一个元素
a.begin() , a.end() ; // a 的迭代器
// vector的遍历方式 :
for(int i = 0;i < 10;i ++ ) cout << a[i] << endl ;
// 注意这里的 迭代器 相当于一个指针 输出的时候需要解引用
for(vector<int>::iterator i = a.begin(); i != a.end() ;i ++ ) cout << *i << endl ;
// auto( 让系统直接推断变量的类型 ) 遍历 是 c++中一种新的遍历方法
for(auto i = a.begin(); i != a.end() ;i ++ ) cout << *i << endl ;
for(auto x : a) cout << x << endl ;
// 支持比较运算 比较规则 -- 按字典序来进行比较
vector<int> a(4,3) , b(3,4) ;
if(a < b) cout << "YES" << endl ; // 程序运行后输出YES
pair<int,int> p ; // 两个数据类型可以任意
p.first , p.second ; // 第一个元素和第二个元素
// 支持比较运算 比较的时候 , 以first为第一关键字 , second为第二关键字 也是字典序
p = make_pair(10,10) ; // 构造一个pair
p = {
10,10} ; // 也可以直接赋值 构造函数的显式转换
// pair也可以用来存储 3 种属性 -- 直接叠加 一次类推
pair<int,pair<int,int>> p ;
// string的
string S ;
S.size() , S.length() ; // 返回字符串的字符个数
S.empty() ; S.clear() ; // 判断是否为空 清空
// string类型的字符串可以直接拼接 +=
string a = "YES" ; a += "def" ; a += "c" ;
cout << a << endl ; // YESdefc
a.substr() ; //作用: 返回一个子串 第一个参数是子串的起始位置,第二个参数是子串的长度
cout << a.substr(1,2) << endl ; // ES
// 当输入的第二个参数超过我们的数组的长度或者省略第二个参数的时候 , 输出从该子串的起始位置到主串的末尾位置
cout << a.substr(1,10) << endl ; // ESdefc
cout << a.substr(1) << endl ; // ESdefc
// 当我们想通过printf输出string类型变量的时候 其实是输出其首地址 这时c_str()函数就是返回string类型变量的首地址
printf("%d",a.c_str()) ;
// queue队列的基本用法 :
queue<int> q ;
q.push() ; // 向队尾插入一个元素
q.front() ; q.back() ; // 返回q的队头 队尾元素
q.pop() ; // 弹出队头元素
q.size() ; q.empty() ;
// 注意 : queue没有clear函数
// 如果想清空 q 可进行如下操作:
q = queue<int>() ;
// priority_queue 优先队列( 堆 ) 的基本用法 :
priority_queue<int> pq ;
pq.push() ; // 向堆中插入一个元素
pq.top() ; // 返回堆顶元素
pq.pop() ; // 弹出堆顶元素
// 注意 : 优先队列也无clear函数
// 注意 : 一般定义的堆默认是大根堆
// 如果要创建一个小根堆 , 可进行如下操作 :
// 1. 在向堆中插入元素的时候 , 直接插入 -x
heap.push(-x) ;
// 2. 在定义的时候直接定义小根堆
priority_queue<int,vector<int>,greater<int>> p ; // 此时 p 为小根堆
// stack 栈
stack stk ;
stk.push() ;// 向栈顶压入一个元素
stk.top() ; // 返回栈顶的元素
st.pop() ; // 将栈顶元素弹出
// 无 clear 函数
// deque 双端队列 有clear函数
deque d ;
d.push_front() ; d.pop_front() ;
d.push_back() ; d.pop_back() ;
d.begin() ; d.end() ; // 迭代器 ;
// 缺点 : 速度慢 速度低 不常用 比一般的数组低好几倍
// set . multiset 基于平衡二叉树(红黑树) , 动态维护有序序列
// beigin() , end() ++ , -- 返回前驱和后继 前面一个数和后面一个数 logN
// set 的所有操作的时间复杂度为 logN 支持 clear
// insert() 插入一个数
// find() 查找一个数 , 如果不存在返回 end迭代器 ;
// count() 返回某一个数的个数
// erase() 输入的是一个数, 删除是这个数的所有结点 O(k + logN)
// 输入的是是一个迭代器 , 删除的是这一个迭代器
// set 最核心的操作 :
// lower_bound() / upper_bound()
// lower_bound(x) 返回大于等于 x 的最小的迭代器 如果不存在返回end
// upper_bound(x) 返回大于x的最小的迭代器 如果不存在返回end
set<int> se ;
multiset<int> mse ;
// map . multimap 存储的是一个映射
// insert() 输入的是一个pair()
// erase() 输入的参数是pair或者迭代器
// find() 和set中的find() 一样
// [] 可以像用数组一样来用map 时间复杂度是 logN
map<string,int> a ;
a["yxc"] = 1 ;
cout << a["yxc"] << endl ; // 1
// unordered_set . unorder_map . unordered_multiset . unordered_multimap
// 和上面类似 优点 : 增删改查的时间复杂度是 O(1)
// 缺点 : 不支持 lower_bound 和 upper_bound 函数 因为其是无序的
// 不支持迭代器的 ++ --
// bitset 压位
// 主要特点 : 存储 bool 类型的数组的时候 , 可以省8位空间
// count 返回有多少个 1
// noen 判断是否全为 0
// set 把所有位置置为 1
// set(k,v) 将第 k 位变成 v
// reset() // 把所有位变成 0
// flip 等价于 ~ 取反
// flip(k) 把 第 k 位取反
return 0 ;
}