2019 南昌区域赛 M. XOR Sum（拉格朗日插值（模板纠正））

---

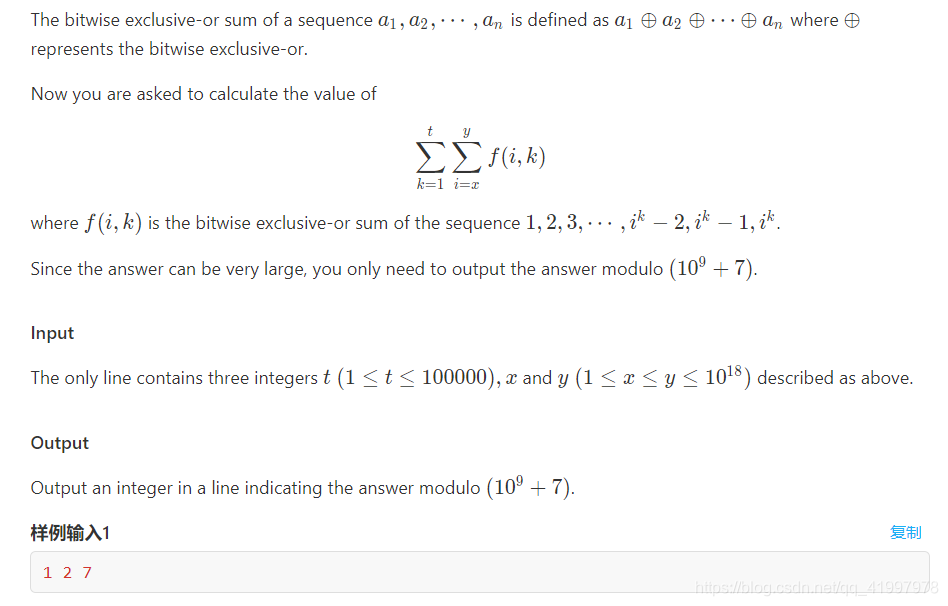
很明显 $f(i,k)$ 是有规律的，因为连续的数字异或，连续的两项异或得到一，打表可以发现：
k = 1

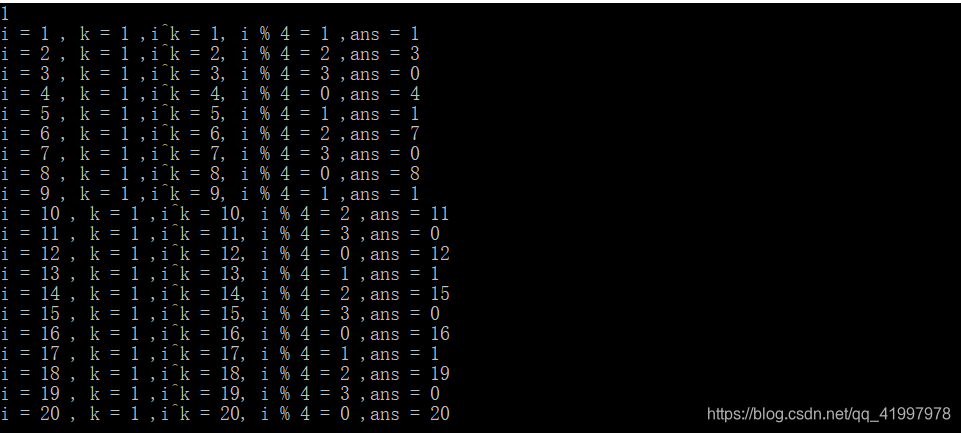
k = 2

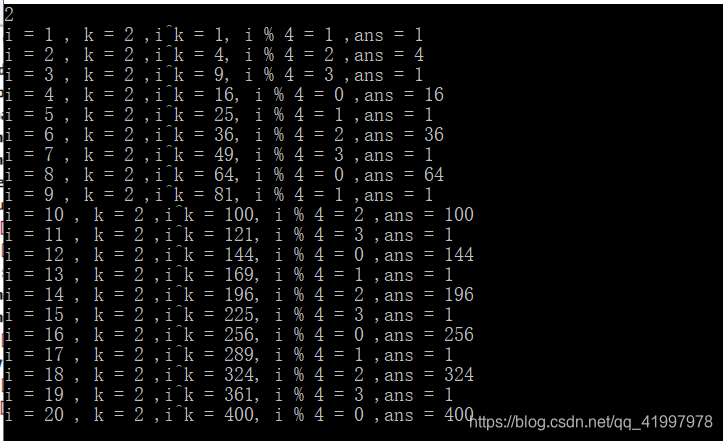
k = 3

根据 k 的奇偶以及 i % 4 的余数进行分类讨论，当 i % 4 = 2 时，贡献为：
$$f(n)=\sum _{k=1}^t{2}^k\sum _{i=1}^{\lfloor \frac{n}{2}\rfloor }{i}^k$$
右边是一个 k + 1 次多项式，可以拉个朗日插值求解，但直接做复杂度是 $t^2$

考虑更改枚举项，得到：
$$f(n)=\sum _{i=1}^{\lfloor \frac{n}{2}\rfloor }\sum _{k=1}^t{2}^k{i}^k$$
右边仍然是一个多项式，是一个以 i 为自变量的 t 次多项式，因此 $f(n)$ 是一个以 n 为自变量的 $t+1$ 次多项式，右边式子是一个等比数列的求和形式，可以在 $O(\log )$ 时间求得，$f(n)$ 的插值可以在 $O(t\log )$ 时间内求解，其它情况的贡献都可以在 O(1) 时间内求得。

注意这里插值的写法不能预处理 ${\prod }_{i=1}^n(x-x_i)$，计算时乘上 $x-x_i$ 的逆元来插值，因为 $x$ 非常大，$x-x_i$ % mod 可能为0导致计算的结果不正确。

---

代码：

#include<iostream>
using namespace std;
typedef long long ll;
#define LL long long
const int mod = 1e9 + 7;
const int maxn = 1e6 + 10;
ll t,x,y,mx;
ll g[maxn],fac[maxn],ifac[maxn];
ll pre[maxn],suf[maxn];
inline ll add(ll x, ll y) {
    
    
  	x += y;
  	if (x >= mod) {
    
    
    	x -= mod;
  	}
  	return x;
}

inline ll sub(ll x,ll y) {
    
    
  	x -= y;
  	if (x < 0) {
    
    
    	x += mod;
  	}
  	return x;
}

inline ll mul(ll x, ll y) {
    
    
  	return x * y % mod;
}
ll fpow(ll a,ll b) {
    
    
	ll r = 1;
	while (b) {
    
    
		if (b & 1) r = mul(r,a);
		a = mul(a,a);
		b >>= 1;
	}
	return r;
}
ll cal(ll g[maxn],ll x) {
    
    			//拉格朗日插值计算多项式
	if (x <= mx) return g[x];
	ll tmp = 1,inv,ans = 0; 
	suf[mx + 1] = pre[0] = 1; 
	for (int i = 1; i <= mx; i++) {
    
    
		pre[i] = mul(pre[i - 1],(x - i) % mod);
	}
	for (int i = mx; i >= 1; i--) {
    
    
		suf[i] = mul(suf[i + 1],(x - i) % mod);
	}
	for (int i = 1; i <= mx; i++) {
    
    
		ll res = 1;
		res = mul(res,g[i]);
		res = mul(res,ifac[i - 1]);
		res = mul(res,ifac[mx - i]);
		res = mul(res,pre[i - 1]);
		res = mul(res,suf[i + 1]);
		if ((mx - i) & 1) ans = sub(ans,res);
		else ans = add(ans,res);
	}
	return ans;
}
ll M(ll x,ll y) {
    
    
	if (y == 0) return x / 4;
	return (x / 4 + (x % 4 >= y)) % mod;
}
ll solve(ll x) {
    
    
	ll ans = 0;
	ans = M(x,1) * (t % mod) % mod;
	ans = (ans + M(x,3) * (t / 2 % mod) % mod) % mod;
	ans = (ans + M(x,2)) % mod;
	ans = (ans + cal(g,x / 2)); 
	return ans;
}
int main() {
    
    
	fac[0] = 1;
	for (int i = 1; i <= maxn - 10; i++)
		fac[i] = mul(fac[i - 1],i);
	ifac[maxn - 10] = fpow(fac[maxn - 10],mod - 2);
	for (int i = maxn - 10 - 1; i >= 0; i--)
		ifac[i] = mul(ifac[i + 1],i + 1);
	scanf("%lld%lld%lld",&t,&x,&y);
	mx = t + 10;
	g[0] = 0;
	for (int i = 1; i <= mx; i++) {
    
    
		ll res = (2 * i % mod - fpow(2 * i % mod,t + 1) + mod) % mod * fpow((1 - 2 * i % mod + mod) % mod,mod - 2) % mod;
		g[i] = (g[i - 1] + res) % mod;
	}
	printf("%lld\n",(solve(y) - solve(x - 1) + mod) % mod);
	return 0;
}