数论入门
- 素数
质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。 - 欧拉函数
在数论,对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目(因此φ(1)=1)。例如φ(8)=4,因为1,3,5,7均和8互质。
若n是质数p的k次幂,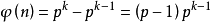
因为除了p的倍数外,其他数都跟n互质。 - 费马定理
费马小定理(Fermat’s little theorem)是数论中的一个重要定理,在1636年提出。如果p是一个质数,而整数a不是p的倍数,则有a^(p-1)≡1(mod p) - 欧拉定理
在数论中,欧拉定理,(也称费马-欧拉定理)是一个关于同余的性质。欧拉定理表明,若n,a为正整数,且n,a互质,则:
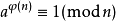
- 素性测试算法
对于一个数n,如果想要判断它是否为素数,常规的方法为试除法。即,让n依次除以2到sqrt(n)以内的整数。如果有出现除尽的情况,则为合数。
实际素性测试中,使得错误可能性小于2-80检测的次数(安全次数S) - CRT,中国剩余定理
物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?即,一个整数除以三余二,除以五余三,除以七余二,求这个整数。《孙子算经》中首次提到了同余方程组问题,以及以上具体问题的解法,因此在中文数学文献中也会将中国剩余定理称为孙子定理。
CRT说明:某一范围内的整数可以通过他的一组剩余类来重构,这组剩余类是对该整数用一组两两互素的整数取模得到 - ** 离散对数问题**
方程y=gxmod p,对给定g,x和p,可直接计算y,对多执行x次乘法,且才能在有效算法
给定y,g和p,计算x一般非常困难,即求离散对数,其难度与RSA中因子分解素数之积有相同难度数量级
已知的最快求模数为素数的离散对数的算法,难度阶为:e^((lnp) 1/3 (ln(lnp))2/3)对大素数该算法不可行。
公钥密码体制基本模型
对称密码体制的局限性
- 密钥分配问题:通信双发要进行加密通信,需要通过秘密的安全信道协商加密密钥,而这种安全信道可能很难实现
- 密钥管理问题:在有多个用户的网络中,任何两个用户之间都需要有共享的密钥,当网络中的用户n很大时,需要管理的密钥数目非常大
N个用户之间通信密钥管理问题:每个用户保存N-1个密钥,总共管理N(N-1)/2个秘钥 - 难以实现不可否认功能:当用户A收到用户B的消息时,无法向第三方证明此消息的来源确实是B,也无法防止事后B否认发送过信息
非对称密码的算法是基于数学函数的,而不是建立在字符或位方式操作上的
与对称密码加解密使用同一密钥不同,非对称密码使用两个独立的密钥,且加密密钥可公开,因此又称公钥密码体制
单向陷门函数
如果函数f(x)被称为单向陷门函数,必须满足一下三个条件:
- 给定x,计算y=f(x)是容易的
- 给定y,计算x使得y=f(x)是困难的
- 存在σ,已知σ时对给定的任何y,若相应的x存在,则计算x使得y=f(x)是容易的
公钥密码体制的性质
- 机密性:通过数据加密来保证非授权人员不能获得机密信息
- 数据完整性:通过数字签名来保证信息内容不会被篡改或替换
- 认证:通过数字签名来验证对方的真实身份
- 不可抵赖性:通过数字签名来实现,是发送者不能事后否认他发送过信息,消息的接受者可以向第三方证实发送者确实发送了消息
RSA算法即安全性分析
RSA既能用于加密,又能用于数字签名,易于理解和实现,是第一个安全、使用的公钥密码体制
RSA的基础是数论的欧拉定理,他的安全性依赖于大整数的因式分解的困难性
RSA安全-明文操纵
- 攻击者已知公钥{e,n}
- 攻击者捕获密文y
- 攻击者替换y为Sey
- 攻击者虽无法解密,但接受方得到是被操纵后的明文