2018 NOIP 提高组 复赛 day1

T1 铺设道路

题目点击→洛谷 P5019 铺设道路
题目描述
春春是一名道路工程师，负责铺设一条长度为 nn 的道路。

铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 $n$ 块首尾相连的区域，一开始，第 $i$ 块区域下陷的深度为 $d_i$

春春每天可以选择一段连续区间 $[L,R]$ ，填充这段区间中的每块区域，让其下陷深度减少 $1$。在选择区间时，需要保证，区间内的每块区域在填充前下陷深度均不为 $0$ 。

春春希望你能帮他设计一种方案，可以在最短的时间内将整段道路的下陷深度都变为 $0$ 。

输入输出格式
输入格式：
输入文件包含两行，第一行包含一个整数 $n$，表示道路的长度。 第二行包含 $n$ 个整数，相邻两数间用一个空格隔开，第 $i$ 个整数为 $d_i$

输出格式：
输出文件仅包含一个整数，即最少需要多少天才能完成任务。

输入输出样例
输入样例#1：
6
4 3 2 5 3 5
输出样例#1：
9

【样例解释】

一种可行的最佳方案是，依次选择：$[1,6]$、$[1,6]$、$[1,2]$、$[1,1]$、$[4,6]$、$[4,4]$、$[4,4]$、$[6,6]$、$[6,6]$。

【数据规模与约定】

对于 $30\%$ 的数据，$1\le n\le 10$ ；
对于 $70\%$ 的数据，$1\le n\le 1000$ ；
对于 $100\%$ 的数据，$1\le n\le 100000,0\le d_i\le 10000$

T1 分析

常规送分题。考虑第一个位置的，这个位置是 $a[0]$ ，那么这个位置必定要被填 $a[0]$ 次才能填平，然后考虑第二个位置，这个位置是 $a[1]$ ，显然如果这个位置比 $a[0]$ 小，那么在填 $a[0]$ 的时候 $a[1]$ 也可以被填平，如果这个位置比 $a[0]$ 大，那么显然 $a[1]$ 中的 $a[0]$ 部分已经可以被填掉了，那么只要多加 $a[1]-a[0]$ 次就可以填平 $a[1]$。

所以做法就出来了，从前往后填坑，保证到第 $i$ 个位置的时候，前$i-1$个都被填满了，那么显然第 $i$ 个位置中高度为$a[i-1]$的部分是不需要被填的，只需要填超出$a[i-1]$的部分就可以了。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
int main()
{
	int n;cin>>n;
	int ans = 0,now = 0;
	for (int i = 0 ; i < n ; ++i){
		int x;cin>>x;
		ans+= max(0,x - now);
		now = x;
	}
	cout<<ans<<endl;
	return 0;
} 

T2 货币系统

题目点击→洛谷 P5020 货币系统
题目描述
在网友的国度中共有 $n$ 种不同面额的货币，第 $i$ 种货币的面额为 $a[i]$，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 $n$、面额数组为 $a[1..n]$ 的货币系统记作 $(n,a)$。

在一个完善的货币系统中，每一个非负整数的金额 $x$ 都应该可以被表示出，即对每一个非负整数 $x$，都存在 $n$ 个非负整数 $t[i]$ 满足 $a[i]\times t[i]$ 的和为 $x$。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 $x$ 不能被该货币系统表示出。例如在货币系统 $n=3$, $a=[2,5,9]$ 中，金额 $1,3$ 就无法被表示出来。

两个货币系统 $(n,a)$ 和 $(m,b)$ 是等价的，当且仅当对于任意非负整数 $x$，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 $(m,b)$，满足 $(m,b)$ 与原来的货币系统 $(n,a)$ 等价，且 $m$ 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 $m$。

输入输出格式
输入格式：
输入文件的第一行包含一个整数 $T$，表示数据的组数。

接下来按照如下格式分别给出 $T$ 组数据。 每组数据的第一行包含一个正整数 $n$。接下来一行包含 $n$ 个由空格隔开的正整数 $a[i]$。

输出格式：
输出文件共有 $T$ 行，对于每组数据，输出一行一个正整数，表示所有与 $(n,a)$ 等价的货币系统 $(m,b)$ 中，最小的 $m$。

输入输出样例
输入样例#1：
2
4
3 19 10 6
5
11 29 13 19 17
输出样例#1：
2
5

T2 分析

照例的$day1$简单题，普及组第2题到第3题的难度。

稍微估计一下分数区，纯暴力dfs应该可能只有15分，加上优化之类的奇奇怪怪的操作应该能到30分~40分。

当然如果意识到一个点：货币系统B一定是货币系统A的子集，也就是所有钱币的数量都来自于A集合，那么就算dfs应该也可以到达80分。

这里有一点，其实前50分的数据范围就是在提醒你是这件事了,小数据却是非常大的$a_i$，大数据$a_i$却变小 : $a_i\le 1000$

显然n小的数据通过放大$a_i$来限制分数，因为你没有发现这道题需要你去发现的点，而发现了这个点的人一定可以通过前50分的数据，所以后50分就不再关注$a_i$，当然这就是自己想想的…不要把这个当成判断题目做法的依据，这只能作为你让自己相信你的做法没有问题的一个非常小的理由。

如果发现了上面那个点，那就比较简单了，既然B一定是A的子集，那么只要去掉A中能被其他钱币组合出的钱币就可以了，也就是简化A，比如A中存在2 3 5三种钱币，显然5可以由2 + 3组成，那就不需要5了。

所以就是个简单的完全背包，标记一下哪些钱币能出现就可以了。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;

int f[25500],a[1500];

int main()
{
	int pp;scanf("%d",&pp);
	while (pp--){
		int n;scanf("%d",&n);
		int M = 0;
		for (int i = 0 ; i < n ; ++i) scanf("%d",&a[i]),M = max(M,a[i]);
		
		memset(f,0,sizeof(int) * (M + 5));
		f[0] = 1;
		for (int i = 0 ; i < n ; ++i)
			for (int j = a[i] ; j <= M ; ++j)
				f[j] += f[j - a[i]];
		
		int ans = n;
		for (int i = 0 ; i < n ; ++i)
			if (f[a[i]] > 1) 
				--ans;
		printf("%d\n",ans);
	}
	return 0;
} 

T3 赛道修建

题目点击→洛谷 P5021 赛道修建
题目描述
C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 $m$ 条赛道。

C 城一共有 $n$ 个路口，这些路口编号为 $1,2,\dots ,n$，有 $n-1$ 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 $i$ 条道路连接的两个路口编号为 $a_i$ 和 $b_i$ ，该道路的长度为 $l_i$ 。借助这 $n-1$ 条道路，从任何一个路口出发都能到达其他所有的路口。

一条赛道是一组互不相同的道路 $e_1,e_2,\dots ,e_k$ ，满足可以从某个路口出发，依次经过 道路 $e_1,e_2,\dots ,e_k$（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。

目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的 $m$ 条赛道中长度最小的赛道长度最大（即 $m$ 条赛道中最短赛道的长度尽可能大）

输入输出格式
输入格式：
输入文件第一行包含两个由空格分隔的正整数 $n,m$ ，分别表示路口数及需要修建的 赛道数。

接下来 $n-1$ 行，第 $i$ 行包含三个正整数 $a_i,b_i,l_i$ ，表示第 $i$ 条适合于修建赛道的道路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 $n-1$ 条道路相互到达。每行中相邻两数之间均由一个空格分隔。

输出格式：
输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

输入输出样例
输入样例#1：
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7
输出样例#1：
31
输入样例#2：
9 3
1 2 6
2 3 3
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4
输出样例#2：
15

T3 分析

最后一题，需要一点思维性的东西。乍一眼一看就猜得出来肯定可以二分答案，那么问题就是check()怎么写了。

首先分析一下数据范围。

可以发现最显眼的一个条件就是 $b_i=a_i+1$

1、 $b_i=a_i+1$ 的情况（一条链）

解法：把所有边权记录下来，这种情况等价于将序列分割成 $m$ 段，使 $m$ 段区间和的最小值最大

那么二分 $m$ 段区间和的最小值，然后 $O(n)$ 贪心扫一遍，时间复杂度 $O(nlogn)$

2、$a_i=1$ 的情况
即这棵树的的深度为2，把所有边权记录下来，从大到小排序。设边权为 $w$，答案即为 $w_1+w_{2m-1},w_2+w_{2m-2},...,w_m+w_{m+1}$的最小值，时间复杂度 $O(nlogn)$

3、 $m=1$ 的情况（树的直径）
解法：取一条最长链，即为树的直径问题，记录一下最大值和次大值，每次把最大 值传到它的父亲，时间复杂度 $O(n)$

以上的情况全部考虑到的话就可以获得55分及以上了，那么这是找规律和暴力做的情况。
然后是第4种情况
4、分支不超过3 （最多是二叉树）
这种情况下对于某个长度要求 $k$ 只有两种情况，对于任意一个点$now$的两个儿子有以下情况

• $val\ge k$
• $va{l}_a+va{l}_b\ge k$

也就是说
要么 $now$ 的某个儿子节点能够形成的最长路已经满足需求长度$k$了，那么这条路就可以自成一条路，答案+1。
要么这个点的两个儿子节点能够形成的最长路都不满足需求长度$k$，但是如果把两个儿子节点的路通过节点 $now$ 连起来形成一条更长的路的长度可以满足需求，那么这也是满足情况的。（当然第二种情况其实包含了第一种情况）

从这里我们可以发现一个问题，对于分支不超过3的节点是这样的，那么如果超过3呢？
显然我们依旧可以用 $now$ 的儿子节点中任意两个点 $x,y$ 满足 $va{l}_x+va{l}_y\ge k$ 拼出满足条件的路。
那么要拼出更多的路，显然就是贪心了。
只要尽量去拼出刚好满足条件的路就可以了。也就是对于任意一条边，选择另一条长度最小，但能够和这条边拼出满足条件的路,即对于点x，选择$va{l}_x+min(va{l}_y)\ge k$
（当然对于本身儿子节点的路径已经满足要求的点不需要拼接其他的路,即$val\ge k$）

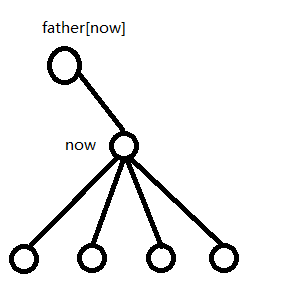
那么现在只剩下一个问题，那就是如何考虑对 $now$ 的父亲 $father[now]$ 来说 $now$ 的最长路。
这里我们可以发现，首先能够满足条件的边一定已经被选走,跟之后的操作已经无关了。
那么对于 $now$ 的儿子节点里，剩下的就只有本身最长路径不满足k，并且还不能跟其他的兄弟路径拼出满足条件的路。
可以发现这些边，虽然通过$now$并不能拼出满足条件的路，但是更往上，到他们祖先节点，就有可能满足条件了。
但是我们也可以发现，因为所有需要到达$now$连向儿子节点的路，都需要经过$edge[father[now]][now]$，但是一条边只能使用一次，所以 $now$ 连向儿子的路中，只能选择一条使用，加上$edge[father[now]][now]$从而形成对于$father[now]$ 来说 $now$ 的最长路。

那么就是代码的事情了，我们二分修建的$m$条路中最短的长度$k$,然后用上面的方法check能否生成m条或以上的路满足长度≥k。这里为了方便组合两条边，我们可以使用multiset,时间复杂度 $O(nlo{g}^{2}n)$
当然这里存在一个小问题，第8组数据，当$a_i=1$时，如果二分的边界$l,r$用极大值$l=0,r=500000000$ 的话就会超时，因为每次check的复杂度都是$n\ast logn$，而二分次数是log(500000000) 所以会超时。
如果没有注意到这一点，嫌麻烦直接写了个极大值边界，就只能95分

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <set>
#include <vector>
using namespace std;

int head[50100],to[100100],nex[100100],val[100100];
int n,waysnumber,m,edges;

multiset <int> :: iterator it;

int dfs(int now,int father,int x){
	multiset <int> son;
	for (int v = head[now]; v ; v = nex[v])
		if (to[v] != father){
			int tmpways = dfs(to[v],now,x) + val[v];
			if (tmpways >= x) ++waysnumber;
			else son.insert(tmpways);
		}	
	//对当前点now的所有子路径进行组合，用刚好能满足≥x的最小的边组合
	//并返回所有儿子中最长的无法被组合成满足条件路的点 
	int maxwaylen = 0;
	while (son.size() > 1){
		it = son.lower_bound(x - *son.begin());
		if (it == son.begin()) it++; //若最短的边≥x的时候，则用最短的两条边组合 
		if (it == son.end()){        //当前最短的边没办法找到够长的边组合出满足条件的路 
			//挑一条最长的子边返回 
			maxwaylen = max(maxwaylen,*son.begin());
			son.erase(son.begin());
		}
		else{
			//成功组合出了满足条件的边 
			++waysnumber;
			son.erase(it);
			son.erase(son.begin());
		}
	}
	if (son.size() == 1) maxwaylen = max(maxwaylen,*son.begin());
	return maxwaylen;
}
 
bool check(int x){
	waysnumber = 0;
	dfs(1,0,x);
	if (waysnumber >= m) return true;
	else return false;
}

void addedge(int u,int v,int c){
    nex[++edges] = head[u], head[u] = edges, to[edges] = v, val[edges] = c;
}

int main()
{
	edges = 0;
	scanf("%d%d",&n,&m);
	long long all = 0;
	for (int i = 1 ; i < n ; ++i){
		int a,b,c;scanf("%d%d%d",&a,&b,&c);
		addedge(a,b,c);
		addedge(b,a,c);
		all += c;
	}
	int l = 0 , r = all / m,mid,ans;   //这里存在一个坑，对于ai = 1的图，如果这里的 r 使用极大值500000000，就会超时
	while (l <= r){
		mid = (l + r) >> 1;
		if (check(mid)) ans = mid,l = mid + 1;
		else r = mid - 1;
	}
	printf("%d\n",ans);
	return 0;
}