NOIP 2017 普及组

T1 成绩

题目点击→计蒜客 [NOIP2017] 成绩

题目描述
牛牛最近学习了 C++ 入门课程，这门课程的总成绩计算方法是：

总成绩=作业成绩 $\times 20\%$ + 小测成绩 $\times 30\%+$ 期末考试成绩 $\times 50\%$

牛牛想知道，这门课程自己最终能得到多少分。

输入格式

输入只有 $1$ 行，包含三个非负整数 $A$ 、 $B$ 、$C$ ，分别表示牛牛的作业成绩、小测成绩和期末考试成绩。相邻两个数之间用一个空格隔开，三项成绩满分都是 $100$ 分。

输出格式

输出只有 $1$ 行，包含一个整数，即牛牛这门课程的总成绩，满分也是 $100$ 分。

数据范围

对于 $30\%$ 的数据，$A=B=0$。

对于另外 $30\%$ 的数据，$A=B=100$。

对于 $100\%$ 的数据， $0\le A$、$B$、$C\le 100$ 且 $A$、$B$、$C$ 都是 $10$ 的整数倍。

样例解释

样例1：

牛牛的作业成绩是 $100$ 分，小测成绩是 $100$ 分，期末考试成绩是 $80$ 分，总成绩是 $100\times 20\%+100\times 30\%+80\times 50\%=20+30+40=90$。

样例2：

牛牛的作业成绩是 $60$ 分，小测成绩是 $90$ 分，期末考试成绩是 $80$ 分，总成绩是 $60\times 20\%+90\times 30\%+80\times 50\%=12+27+40=79$。

T1分析

送分题，因为 $a,b,c$ 必然是 $10$ 的倍数，所以不存在小数的情况，直接计算即可

#include <iostream>
using namespace std;
int main(){
    int a, b, c;
    cin >> a >> b >> c;
    cout << a / 10 * 2 + b / 10 * 3 + c / 10 * 5 << endl;
	return 0;
}

T2 图书管理员

题目点击→计蒜客 [NOIP2017] 图书管理员

题目描述
图书馆中每本书都有一个图书编码，可以用于快速检索图书，这个图书编码是一个正整数。

每位借书的读者手中有一个需求码，这个需求码也是一个正整数。如果一本书的图书编码恰好以读者的需求码结尾，那么这本书就是这位读者所需要的。

小 D 刚刚当上图书馆的管理员，她知道图书馆里所有书的图书编码，她请你帮她写一个程序，对于每一位读者，求出他所需要的书中图书编码最小的那本书，如果没有他需要的书，请输出 $-1$ 。

输入格式

输入的第一行，包含两个正整数 $n$ 和 $q$ ，以一个空格分开，分别代表图书馆里书的数量和读者的数量。

接下来的 $n$ 行，每行包含一个正整数，代表图书馆里某本书的图书编码。

接下来的 $q$ 行，每行包含两个正整数，以一个空格分开，第一个正整数代表图书馆里读者的需求码的长度，第二个正整数代表读者的需求码。

输出格式

输出有 $q$ 行，每行包含一个整数，如果存在第 $i$ 个读者所需要的书，则在第 $i$ 行输出第 $i$ 个读者所需要的书中图书编码最小的那本书的图书编码，否则输出 $-1$。

数据范围

对于 $20\%$ 的数据，$1\le n\le 2$ 。 另有 $20\%$ 的数据，$q=1$。

另有 $20\%$ 的数据，所有读者的需求码的长度均为 $1$ 。

另有 $20\%$ 的数据，所有的图书编码按从小到大的顺序给出。

对于 $100\%$ 的数据，$1\le n\le 1,000$，$1\le q\le 1,000$，所有的图书编码和需求码均不超过 $10,000,000$。

样例说明

第一位读者需要的书有 $2123$ 、$1123$、$23$，其中 $23$ 是最小的图书编码。

第二位读者需要的书有 $2123$、$1123$，其中 $1123$ 是最小的图书编码。

对于第三位，第四位和第五位读者，没有书的图书编码以他们的需求码结尾，即没有他们需要的书，输出 $-1$。

T2分析

可以观察到，这道题目的 $n,q$ 都不大，甚至连数字本身也不大，完全可以用 $int$ 解决，所以直接暴力 $O(nq)$ 对每个询问都遍历一遍所有书找出最小的即可
当然这里题目要求我们找最小的那个编号，所以可以加一个小优化，那就是提前排个序，那我们从小到大遍历书，只要找到第一个满足条件的一定就是答案
当然不加也没有影响，注意判断最小即可

#include <iostream>
#include <cmath>
using namespace std;
const int N = 1e3 + 9;
int a[N];
int main(){
    int n, q;
    cin >> n >> q;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    sort(a, a + n);
    while (q--) {
        int x, y;
        cin >> x >> y;
        for (int i = 0; i < n; i++) {
            if (y == a[i] % (int)pow(10, x)) {
                cout << a[i] << endl;
                break;
            }
            if (i == n - 1) {
                cout << -1 << endl;
            }
        }
    }
	return 0;
}

T3 棋盘

题目点击→ 计蒜客 [NOIP2017] 棋盘

题目描述
有一个 $m\times m$ 的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的），你只能向上、下、左、右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 $1$ 个金币。

另外，你可以花费 $2$ 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用，而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法；只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入格式

数据的第一行包含两个正整数 $m$，$n$，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的 $n$ 行，每行三个正整数 $x$ ，$y$，$c$，分别表示坐标为（$x$，$y$）的格子有颜色 $c$。其中 $c=1$ 代表黄色，$c=0$ 代表红色。相邻两个数之间用一个空格隔开。棋盘左上角的坐标为（ $1,1$ ），右下角的坐标为（ $m,m$ ）。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是（$1,1$）一定是有颜色的。

输出格式

输出一行，一个整数，表示花费的金币的最小值，如果无法到达，输出 $-1$ 。

数据范围

对于 $30\%$ 的数据，$1\le m\le 5$， $1\le n\le 10$。

对于 $60\%$ 的数据，$1\le m\le 20$， $1\le n\le 200$。

对于 $100\%$ 的数据，$1\le m\le 100$， $1\le n\le 1,000$。

样例说明

样例1：

从（$1$，$1$）开始，走到（$1$，$2$）不花费金币从（$1$，$2$）向下走到（$2$，$2$）花费 $1$ 枚金币从（$2$，$2$）施展魔法，将（$2$，$3$）变为黄色，花费 $2$ 枚金币从（$2$，$2$）走到（$2$，$3$）不花费金币从（$2$，$3$）走到（$3$，$3$）不花费金币从（$3$，$3$）走到（$3$，$4$）花费 $1$ 枚金币从（$3$，$4$）走到（$4$，$4$）花费 $1$ 枚金币从（$4$，$4$）施展魔法，将（$4$，$5$）变为黄色，花费 $2$ 枚金币，从（$4$，$4$）走到（$4$，$5$）不花费金币从（$4$，$5$）走到（$5$，$5$）花费 $1$ 枚金币共花费 $8$ 枚金币。

样例2：

从（1，1）走到（1，2），不花费金币从（1，2）走到（2，2），花费 1金币施展魔法将（2，3）变为黄色，并从（2，2）走到（2，3）花费 2金币从（2，3）走到（3，3）不花费金币

从（3，3）只能施展魔法到达（3，2），（2，3），（3，4），（4，3）

而从以上四点均无法到达（5，5），故无法到达终点，输出－1

T3分析

这个数据范围明摆着告诉我们是搜索…

解法 I

最容易想到的就是直接暴力 $dfs$
用 $dfs(x,y,sum,flag)$ 来表示到达 $(x,y)$ 这个点花费为 $sum$ ，$flag$ 表示是否使用过魔法
那么直接进行上下左右四个方向，分情况进行搜索即可
但是这种做法显然会超时
所以我们加上最简单的空间换时间的优化——记忆化搜索
用 $f[x][y]$ 来记录曾经到达 $(x,y)$ 这个格子时的最小花费，那么如果后面搜索又到了 $(x,y)$ 但是花费已经超过了 $f[x][y]$ 就没有必要再搜索了
但是这里有个小细节需要注意，当然比赛中大部分人可能都没有细想，那就是为什么这里的数组记录状态只需要 $f[x][y]$?对于空白格来说，显然存在两种情况，到达这个点的时候我用魔法把这个位置变成了红色或者黄色
那这里不是应该用 $f[x][y][a[x][y]]$ 来标记吗？为什么可以不用记录颜色呢，不记录颜色的话不是并不能表示出一个完整的状态了吗？
这里其实是可以证明的，可能出现问题的情况就类似于下图：
中间是空白格子，到达上方和左方两个格子的最小步数都是 $3$，而此时如果我们的搜索顺序是先到了红色格，那么红色格往下移动到空白格，我们会在空白格记录下 $f[x][y]=5$，然后红色再往后移动，到达终点的花费是 $6$,而后面从左方的黄色格搜索到空白格时会发现 $sum=5>=f[x][y]$ 那么就不会继续往后搜索了，最终导致终点的答案为 $6$

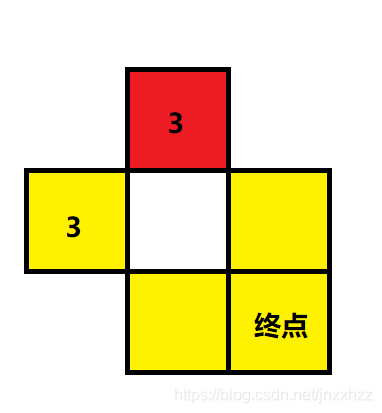
其实是不存在这种情况的，我们可以发现因为起点必然存在颜色，所以起点到任意一个格子的左方和上方的距离是一样的，在同样的距离下，起点和终点的颜色不同就意味着两条路径中变换颜色的次数不一样，而变换颜色的次数不一样则一定会导致到达左方和上方时的花费不同，所以不可能存在上图的这种情况。
从这里也可以看出，其实出题是非常严谨的，很多人可能并不会关注到起点一定有颜色这个条件，这个条件为的就是保证以上这一点！

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9;
const int inf = 0x3f3f3f3f;
int a[N][N], f[N][N];
int dx[] = {
    
    -1, 1, 0, 0};
int dy[] = {
    
    0, 0, -1, 1};
int n, m;

void dfs(int x, int y, int sum, int flag) {
    
    
	if (sum >= f[x][y]) {
    
    
		return;
	}
	f[x][y] = sum;
	if (x == m && y == m) {
    
    
		return;
	}
	for (int i = 0; i < 4; i++) {
    
    
		int tx = x + dx[i];
		int ty = y + dy[i];
		if (tx > 0 && tx <= m && ty > 0 && ty <= m) {
    
    
			if (a[tx][ty]) {
    
    
				dfs(tx, ty, sum + (a[tx][ty] != a[x][y]), 0);
			} else if (!flag) {
    
    
				a[tx][ty] = a[x][y];
				dfs(tx, ty, sum + 2, true);
				a[tx][ty] = 0;
			}
		}
	}
}

int main() {
    
    
	memset(f, inf, sizeof f);
	cin >> m >> n;
	while (n--) {
    
    
		int x, y, z;
		cin >> x >> y >> z;
		a[x][y] = z + 1;
	}
	dfs(1, 1, 0, 0);
	cout << (f[m][m] == inf ? -1 : f[m][m]) << endl;
	return 0;
}

解法 II

用 $priorit{y}_{q}ueue$ 记录到每个点用的最少花费，空白点只可能是通过使用魔法到达的，但是它后面的点必须有颜色，因为是优先队列，所以每个点进入队列一次就可以，后面来的肯定是花费更多了。
这种做法其实就类似于 $dijkstra$ 最短路,所以对于这道题我们也可以直接建边进行最短路搜索

#include <iostream>
#include <cstring>
#include <queue>
 
using namespace std ;
 
const int N = 110 ;
int n , map[N][N] ;
 
struct node {
	int x , y , s , now ; //如果当前格子有颜色，那么now=-1，否则now==改成的颜色  ， 坐标（x,y) 费用s 
	inline bool operator < ( const node &k ) const {
		return  k.s < s  ;
	}
} ;
priority_queue < node > q ;
int dis[N][N] ; //dis记录最小花费 
 
const int dx[4] = { 0 , 0 , 1 , -1 } ;
const int dy[4] = { 1 , -1 , 0 , 0 } ;
 
int main() {
	int t , x , y , c , s , now ; cin >> n >> t ;
	memset ( map , -1 , sizeof(map) ) ;
	while ( t-- ) {
		cin >> x >> y >> c ;
		map[x][y] = c ;
	}
	memset ( dis , 63 , sizeof(dis) ) ; dis[1][1] = 0 ;
	q.push( (node){ 1 , 1 , 0 , -1 } ) ;
	while ( !q.empty() ) {
		x = q.top().x , y = q.top().y , 
		s = q.top().s , now = q.top().now ; //先把这四个记录下来 
		q.pop() ; if ( x == n && y == n ) { cout << s << endl ; return 0 ; } //到终点就直接输出 
		if ( s > dis[x][y] ) continue ; //剪枝 
		for ( int i = 0 ; i < 4 ; i ++ ) {
			int xx = x + dx[i] ; //新的坐标 
			int yy = y + dy[i] ;
			if ( !( 1<=xx && xx<=n && 1<=yy && yy<=n ) ) continue ; //如果超出边界 
			if ( map[xx][yy] == -1 ) { //如果这个点是空格 
				if( now != -1 ) continue ; //如果我是从空格来的，那么就不能到这个格子 
				for ( int j = 0 ; j <= 1 ; j ++ ) { //是把这个格子变成1好还是0好 
					int ss = s + 2 ; //花费+2 
					ss += ( j == map[x][y] ? 0 : 1 ) ; //判断是否要花费1 
					if ( dis[xx][yy] > ss ) { //如果这个是更优解，就往下搜 
						dis[xx][yy] = ss ;
						q.push( (node){ xx , yy , ss , j } ) ;
					}
				}
			}
			else {
				int ss ; //如果不是空格 
				if ( now == -1 ) ss = s + ( map[xx][yy] == map[x][y] ? 0 : 1 ) ; //我从非空格的格子来 
				else ss = s + ( map[xx][yy] == now ? 0 : 1 ) ; //我从空格的格子来 
				if ( dis[xx][yy] > ss ) { //更新 
					dis[xx][yy] = ss ;
					q.push( (node){ xx , yy , ss , -1 } ) ;
				}
			}
		}
	}
	cout << "-1" << endl ; //输出 
	return 0 ;
}

T4 跳房子

点击查看→ 计蒜客 [NOIP2017] 跳房子

题目描述
跳房子，也叫跳飞机，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一。跳房子的游戏规则如下：

在地面上确定一个起点，然后在起点右侧画 $n$ 个格子，这些格子都在同一条直线上。每个格子内有一个数字（整数），表示到达这个格子能得到的分数。玩家第一次从起点开始向右跳，跳到起点右侧的一个格子内。第二次再从当前位置继续向右跳，依此类推。规则规定：玩家每次都必须跳到当前位置右侧的一个格子内。玩家可以在任意时刻结束游戏，获得的分数为曾经到达过的格子中的数字之和。

现在小 R 研发了一款弹跳机器人来参加这个游戏。但是这个机器人有一个非常严重的缺陷，它每次向右弹跳的距离只能为固定的 $d$。小 R 希望改进他的机器人，如果他花 $g$ 个金币改进他的机器人，那么他的机器人灵活性就能增加 $g$，但是需要注意的是，每次弹跳的距离至少为 $1$ 。具体而言，当 $g<d$ 时，他的机器人每次可以选择向右弹跳的距离为 $d-g,d-g+1,d-g+2,\dots ,d+g-2,d+g-1,d+g$；否则（当 $g\ge d$ 时），他的机器人每次可以选择向右弹跳的距离为 $1,2,3,\dots ,d+g-2,d+g-1,d+g$。

现在小 $R$ 希望获得至少 $k$ 分，请问他至少要花多少金币来改造他的机器人。

输入格式

第一行三个正整数 $n$，$d$，$k$，分别表示格子的数目，改进前机器人弹跳的固定距离，以及希望至少获得的分数。相邻两个数之间用一个空格隔开。

接下来 $n$ 行，每行两个正整数 $x_i$ , $s_i$ ，分别表示起点到第 $i$ 个格子的距离以及第 $i$ 个格子的分数。两个数之间用一个空格隔开。保证 $x_i$ 按递增顺序输入。

输出格式

共一行，一个整数，表示至少要花多少金币来改造他的机器人。若无论如何他都无法获得至少 $k$ 分，输出 $-1$。

数据范围

本题共 $10$ 组测试数据,每组数据 $10$ 分。

对于全部的数据满足 $1\le n\le 500000$, $1\le d\le 2000$ , $1\le x_i$, $k\le 10^9$, $|s_i|<10^5$ 。

对于第 $1,2$ 组测试数据, $n\le 10$；

对于第 $3,4,5$ 组测试数据, $n\le 500$

对于第 $6,7,8$ 组测试数据, $d=1$

样例说明

样例1：

花费 $2$ 个金币改进后，小 R 的机器人依次选择的向右弹跳的距离分别为 $2$，$3$，$5$，$3$，$4$， $3$，先后到达的位置分别为 $2$，$5$，$10$，$13$，$17$，$20$，对应 $1$, $2$, $3$, $5$, $6$, $7$ 这 $6$ 个格子。这些格子中的数字之和 $15$ 即为小 $R$ 获得的分数。

样例2：

由于样例中 $7$ 个格子组合的最大可能数字之和只有 $18$ ，无论如何都无法获得 $20$ 分。

T4分析

前 $20\%$ 的分数不用多说了，这个瞎做做甚至 $dfs$ 暴力都能获得

观察数据范围，可以发现能通过的算法大概是 $O(nlogn)$ 左右复杂度的代码
那么我们做题目没有必要一开始就想到怎么做正解，我们慢慢来思考
首先最简单的，这道题我们可以用一个三重循环暴力去做
从小到大枚举花费的金币 $g$，对于每次 $g$ 我们可以求得机器人能移动的区间 $[max(1,d-g),d+g]$
那么很容易发现这不就是一个直观的动态规划吗？
每个格子可以由前面某一段区间内跳过来，问能否存在方案使得得分 $\ge k$
那么我们可以设 $dp[i]$ 跳到第 $i$ 个格子时的最大得分
那么很容易找到状态转移方程 $dp[i]=max(dp[i-j])+s[i](max(1,d-g)\le j\le d+g)$
那么我们接下来对于一个确定的 $g$ 用双重循环直接暴力去做这个 $dp$，判断中途是否有方案的得分 $\ge k$，只要存在这种方案，当前的 $g$ 就是答案，这是 $O(n^3)$ 的暴力，能做到第四题的同学应该不难想到这个做法，这个做法可以获得 $50\%$ 的分数甚至更多

那么有了基础的做法，我们就要思考如果加快我们的算法了，这份代码主要优化就是这三个循环 $n$
我们一个一个来考虑，首先我们很容易发现 $g$ 越大，越容易找到答案，而这一定是个递增的序列，所以这个 $g$ 必然是可以用 二分答案 来做的，显然这个枚举 $g$ 的循环被优化成了 $O(logn）$的复杂度，那么现在的复杂度就变成了 $O(n^{2}logn)$

看一下我们预估的算法复杂度可以发现，我们需要再优化掉一个 $n$，那优化的地方就不用说了，肯定是优化这个二维的 $dp$

那么方向找到了，优化的地方就容易看出来了，首先枚举 $1\sim n$ 这是必然的，因为我们必须一个点一个点走，那么能优化的地方就是这个寻找前面这段区间的最优解了,对于 $dp[i]$，我们需要找到的就是前面 $[max(1,d-g),d+g]$ 这段区间中最大的 $dp$，那么如何来维护这段信息呢？

单调队列，我们可以发现，当 $i$ 向后移动的同时，这个区间其实也在同时向后移动，那我们需要的一直都是这段区间中的最大值，所以我们维护一个单调队列就可以解决这个问题！

那么现在我们可以用 $O(n)$ 的复杂度完成 $dp$,总体复杂度就是 $O(nlogn)$，跟预想的一样！

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 9;
const ll inf = 1e18;
deque<ll> dq;
ll n, d, k;
ll pos[N], w[N], f[N];

void ins(ll x) {
	while (!dq.empty() && f[dq.back()] <= f[x]) {
		dq.pop_back();
	}
	dq.push_back(x);
}

void era(ll x, ll ma) {
	while (!dq.empty() && pos[x] - pos[dq.front()] > ma) {
		dq.pop_front();
	}
}

ll maxdq() {
	return dq.empty() ? -inf : f[dq.front()];
}

bool check(ll g) {
	while(!dq.empty()) {
		dq.pop_front();
	}
    ll mi = max(d - g, 1LL);
    ll ma = d + g;
	ll cnt = 0;
    f[0] = 0;
    for (int i = 1; i <= n; i++) {
		while (pos[i] - pos[cnt] >= mi) {
			ins(cnt++);
		}
		era(i, ma);
		f[i] = maxdq() + w[i];
		if (f[i] >= k) {
			return true;
		}
    }
	return false;
}

int main(){
    cin >> n >> d >> k;
    for (int i = 1; i <= n; i++) {
		cin >> pos[i] >> w[i];
    }
    ll l = 0, r = inf;
    while (l < r) {
        ll m = l + r >> 1;
        if (!check(m)) {
            l = m + 1;
        } else {
            r = m;
        }
    }
    cout << (l == inf ? -1 : l) << endl;
	return 0;
}