快速入门之——乘法逆元求组合数

逆元+快速幂+阶乘求组合数（快速入门）

前言：

大家基本上应该都知道用杨辉三角法求组合数C(n,m)（n为下标）
也就是直接暴力打表求法O(n*m)：

for(int i=0;i<=n;i++){
	c[i][0]=c[i][i]=1;
	for(int j=1;j<i;j++)
		c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}

但是很明显不好，然后就想到了这个公式：

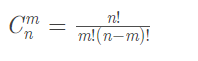
内心独白：对啊，直接用这个公式不就完事了吗，但是要知道，除法是不能求余的，而一般情况下，我们都需要进行求余操作，即：
(a÷b)%c=(a%c÷b%c)%c
上面这种运算是错误的！

这就出现了今天的老大哥：逆元+快速幂+阶乘求组合数

何为逆元？

逆元就是通常所说的：倒数（这就秒懂了吧）

怎么求逆元？

这里得提到费马小定理：

也就是说：a的逆元为a^(p-2)

对于这种幂的运算，就得用到快速幂了
（关于快速幂这里不介绍）

回到主题：

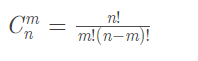
这个公式目前我们就可以转换为：
C(n,m)=n!*inv[m!]*inv[(n-m)!]
（其中：inv表示逆元）

最后发现，阶乘逆元不知道怎么算？

怎么求阶乘逆元？

所以就有：
inv[(n-1)!]=inv[n] * n

直接利用递推即可。

最后关于C(n,m)的求法就大功告成了
C(n,m)=n!*inv[m!]*inv[(n-m)!]

相关代码实现：

#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=1e5+5;
const ll mod=998244353;
ll inv[maxn], fac[maxn];  //分别表示逆元和阶乘
//快速幂
ll quickPow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1)
            ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans;
}

void init(){
    //求阶乘
    fac[0]=1;
    for(int i=1;i<maxn;i++){
        fac[i]=fac[i-1]*i%mod;
    }
    //求逆元
    inv[maxn-1]=quickPow(fac[maxn-1],mod-2);
    for(int i=maxn-2;i>=0;i--){
        inv[i]=inv[i+1]*(i+1)%mod;
    }
}
ll C(int n,int m){
    if(m>n){
        return 0;
    }
    if(m==0)
        return 1;
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main(){
    init();
    int n,m;
    scanf("%d%d",&n,&m);
    printf("%lld\n",C(n,m));
}

参考文章：
https://www.cnblogs.com/kongbursi-2292702937/p/10582258.html
https://blog.csdn.net/qq_40861916/article/details/82928080