牛客多校第9场E Groundhog Chasing Death

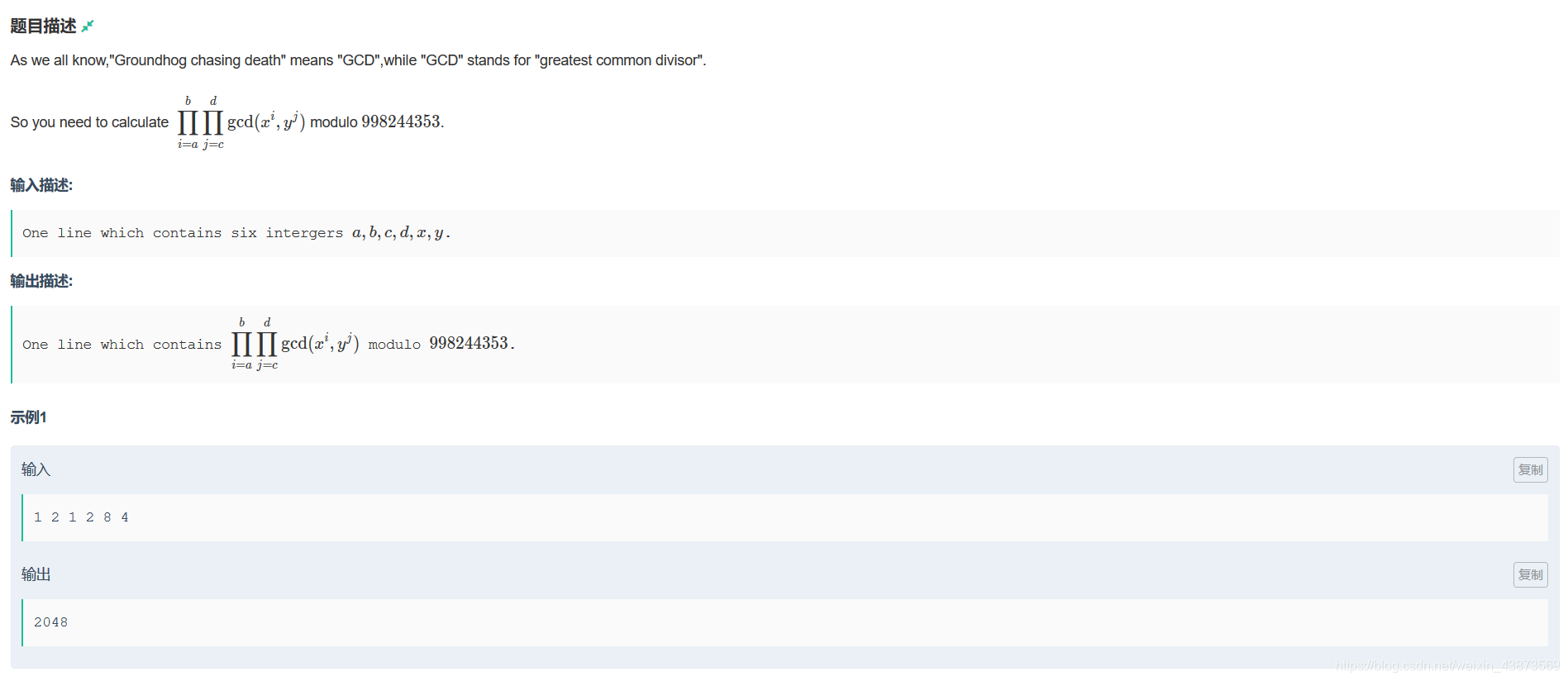
开始以为是什么高深的数论题，后来 重新 推了一下，得到了个这么个式子。
$\prod_{i=a}^b\prod_{j=c}^d (p_1^{min(a_1[1]i,a_2[1]j)}p_2^{min(a_1[2]i,a_2[2]j)}...p_m^{min(a_1[m]i,a_2[m]j)}),$其中 $a_1,a_2$是 $x,y$公共质因数 $p_i$的指数。
那么我们就可以先求 $x,y$的gcd，然后再求得 $a_1,a_2$,进而枚举gcd的质因子和i，复杂度 $O(nlog(n))$。
至于 $min(a_1[k]i,a_2[k]j),k\subseteq[1,m]$，我们需要分类讨论一下， $mid=\frac{a_1[k]i}{a_2[k]}$
1. $mid\subseteq[c,d]，val=(d - mid) * i * a_1+\frac{(mid + c) * (mid - c + 1)} {2}*a_2$
2. $mid>d,val=\frac{(d + c) * (d - c + 1)} {2}*a_2$
3. $mid<c,val=(d - c + 1) * i * a_1$
这里要注意一下，就是要先枚举质因子，再枚举i，避免过多使用快速幂而导致TLE。因为 $p^ap^b=p^{a+b}$,所以我们可以在枚举i的时候，先将指数累加，枚举完i之后，再用一次快速幂，这样复杂度几乎是 $O(n)$的。

#include<bits/stdc++.h>
#define db double
#define ll long long
#define inf 0x3f3f3f3f
#define ms(x,a) memset(x,a,sizeof(x))
#define debug cout<<"***"<<endl
using namespace std;
const int maxn = 3e6 + 10;
const int maxm = 1e5 + 10;
const ll mod = 998244353;
const ll mod1 = 998244352;
int n,m;

ll qpow(ll x,ll n) {
	ll res = 1;
	while(n) {
		if(n & 1)res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}

bool v[maxn];
int cnt;
ll p[maxn];

void init() {
	ms(p,0);
	ms(v,0);
	cnt = 0;
	v[1] = 1;
	for(int i = 2; i < maxn; i++) {
		if(!v[i]) {
			p[++cnt] = i;
		}
		for(int j = 1; j <= cnt && i * p[j] <= maxn; j++) {
			v[i * p[j]] = 1;
			if(i % p[j] == 0) {
				break;
			}
		}
	}
}

ll gcd(ll a,ll b) {
	return b == 0 ? a : gcd(b,a % b);
}

ll pri[maxn],a1[maxn],a2[maxn];

ll calc(ll i,ll a1,ll a2,ll c,ll mid,ll d) {
	ll tmp1 = (d - mid) * i * a1;
	ll tmp2 = ((mid + c) * (mid - c + 1) / 2 ) * a2 ;
	if(mid >= c && mid <= d) {
		return (tmp1 + tmp2) ;
	} else if(mid > d) {
		return ((d + c) * (d - c + 1) / 2 )  * a2 ;
	} else if(mid < c) {
		return ( d - c + 1 ) * i * a1;
	}
}

void solve() {
	init();
	ll a,b,c,d,x,y;
	scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&x,&y);
	ll gkd = gcd(x,y);
	int tot = 0;
	for(int i = 1; p[i] <= gkd; i++) {
		while(gkd % p[i] == 0) {
			pri[++tot] = p[i];
			while(gkd % p[i] == 0) {
				gkd /= p[i];
			}
		}
	}
	if(gkd > 1) {
		pri[++tot] = gkd;
	}
	int cnt1 = 0,cnt2 = 0;
	for(int i = 1; i <= tot; i++) {
		while(x % pri[i] == 0) {
			a1[i]++;
			x /= pri[i];
		}
		while(y % pri[i] == 0) {
			a2[i]++;
			y /= pri[i];
		}
	}
	ll ans = 1;
	for(int j = 1; j <= tot; j++) {
		ll sm = 0; 
		for(ll i = a; i <= b; i++) {
			ll mid = a1[j] * i / a2[j];
			sm = (sm + calc(i,a1[j],a2[j],c,mid,d)) % mod1;
		}
		ans = ans * qpow(pri[j],sm) % mod;
	}
	printf("%lld\n",ans);
}

int main() {
//    ios::sync_with_stdio(false);
//    cin.tie(0);
	solve();
	return 0;
}

//Dawn_Exile