(
h
i
d
d
e
n
/
l
a
t
e
n
t
v
a
r
i
a
b
l
e
)
(hidden/latent \ variable)
( h i d d e n / l a t e n t v a r i a b l e )
E
M
\qquad EM
E M 隐变量
(
h
i
d
d
e
n
v
a
r
i
a
b
l
e
)
(hidden \ variable)
( h i d d e n v a r i a b l e )
[
[
[ 潜在变量
(
l
a
t
e
n
t
v
a
r
i
a
b
l
e
)
(latent \ variable)
( l a t e n t v a r i a b l e )
]
]
] 最大似然估计法
E
M
EM
E M
An elegant and powerful method for finding maximum likelihood solutions with latent variables expectation-maximization algorithm. —— From 《Pattern Recognition and Machine Learning》 § 9.2.2
三硬币问题
A
、
B
、
C
A、B、C
A 、 B 、 C
π
、
p
、
q
\pi、p、q
π 、 p 、 q
A
A
A 硬币
B
B
B
A
A
A 或 硬币
C
C
C
A
A
A ;然后投掷选出的硬币,掷硬币的结果,出现正面记为
1
1
1
0
0
0
N
N
N
N
N
N
(
N
=
10
)
(N=10)
( N = 1 0 )
1
,
1
,
0
,
1
,
0
,
0
,
1
,
0
,
1
,
1
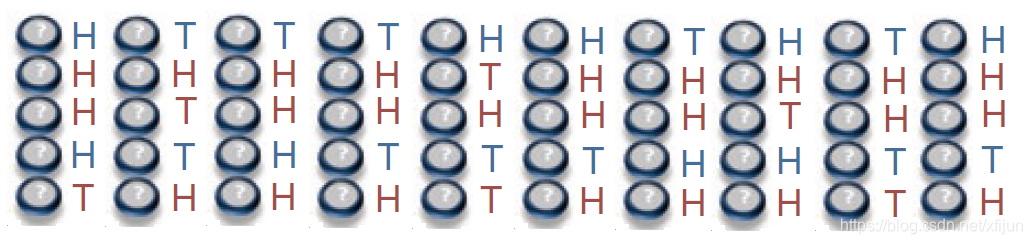
1,1,0,1,0,0,1,0,1,1
1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 只能观测到 掷硬币的结果 无法观测到掷硬币的过程
李航. 《统计学习方法》第9章
\qquad
硬币正面(反面)出现的概率
P
(
y
∣
θ
)
P(y|\theta)
P ( y ∣ θ )
θ
=
(
π
,
p
,
q
)
\theta=(\pi,p,q)
θ = ( π , p , q )
\qquad
\qquad
y
y
y “三硬币问题”的观测变量 :
y
=
1
y=1
y = 1 正面 ;
y
=
0
y=0
y = 0 反面 。那么,
10
10
1 0
{
y
1
,
y
2
,
⋯
,
y
10
}
,
y
n
∈
{
0
,
1
}
\{ y_{1}, y_{2},\cdots,y_{10} \},\ \ y_{n}\in \{0,1\}
{ y 1 , y 2 , ⋯ , y 1 0 } , y n ∈ { 0 , 1 }
\qquad
y
=
1
y=1
y = 1 硬币出现正面 ”的结果 ,但是我们只能知道掷出了硬币的正面,并不知道到底是
硬币
B
的正面
\textbf{硬币\ B\ 的正面}
硬币 B 的正面
z
=
1
z=1
z = 1
硬币
C
的正面
\textbf{硬币\ C\ 的正面}
硬币 C 的正面
z
=
0
z=0
z = 0
\qquad
硬币B 、还是硬币C 来产生 “观测
y
y
y
z
z
z 中间过程 无法观测的
如果单独考虑 投掷硬币
B
(
z
=
1
)
B\ (z=1)
B ( z = 1 )
y
y
y 条件概率 (上图中的第2行),即:
P
(
y
∣
z
=
1
,
θ
)
=
p
y
(
1
−
p
)
(
1
−
y
)
,
y
∈
{
0
,
1
}
\qquad\qquad P(y|z=1,\theta)=p^{y}(1-p)^{(1-y)},\qquad y \in\{0,1\}
P ( y ∣ z = 1 , θ ) = p y ( 1 − p ) ( 1 − y ) , y ∈ { 0 , 1 }
如果单独考虑 投掷硬币
C
(
z
=
0
)
C\ (z=0)
C ( z = 0 )
y
y
y 条件概率 (上图中的第3行),即:
P
(
y
∣
z
=
0
,
θ
)
=
q
y
(
1
−
q
)
(
1
−
y
)
,
y
∈
{
0
,
1
}
\qquad\qquad P(y|z=0,\theta)=q^{y}(1-q)^{(1-y)},\qquad y \in\{0,1\}
P ( y ∣ z = 0 , θ ) = q y ( 1 − q ) ( 1 − y ) , y ∈ { 0 , 1 }
\qquad
\qquad
n
n
n
y
n
y_{n}
y n
如果投掷的是硬币
B
B
B
z
=
1
z=1
z = 1
y
n
y_{n}
y n 联合概率
P
(
y
n
,
z
=
1
∣
θ
)
P(y_{n},z=1|\theta)
P ( y n , z = 1 ∣ θ )
P
(
y
n
,
z
=
1
∣
θ
)
=
P
(
z
=
1
∣
θ
)
P
(
y
n
∣
z
=
1
,
θ
)
=
π
p
y
n
(
1
−
p
)
(
1
−
y
n
)
\qquad\qquad P(y_{n},z=1|\theta)=P(z=1|\theta)P(y_{n}|z=1,\theta)=\pi p^{y_{n}}(1-p)^{(1-y_{n})}
P ( y n , z = 1 ∣ θ ) = P ( z = 1 ∣ θ ) P ( y n ∣ z = 1 , θ ) = π p y n ( 1 − p ) ( 1 − y n )
如果投掷的是硬币
C
C
C
z
=
0
z=0
z = 0
y
n
y_{n}
y n 联合概率
P
(
y
n
,
z
=
0
∣
θ
)
P(y_{n},z=0|\theta)
P ( y n , z = 0 ∣ θ )
P
(
y
n
,
z
=
0
∣
θ
)
=
P
(
z
=
0
∣
θ
)
P
(
y
n
∣
z
=
0
,
θ
)
=
(
1
−
π
)
q
y
n
(
1
−
q
)
(
1
−
y
n
)
\qquad\qquad P(y_{n},z=0|\theta)=P(z=0|\theta)P(y_{n}|z=0,\theta)=(1-\pi)q^{y_{n}}(1-q)^{(1-y_{n})}
P ( y n , z = 0 ∣ θ ) = P ( z = 0 ∣ θ ) P ( y n ∣ z = 0 , θ ) = ( 1 − π ) q y n ( 1 − q ) ( 1 − y n )
\qquad
\qquad
隐藏变量
z
z
z
A
A
A (该过程无法被观测 ) :
⟶
\qquad \longrightarrow
⟶
z
=
1
z=1
z = 1
A
A
A 正面 ,选择 硬币
B
B
B
y
y
y
P
(
y
,
z
=
1
∣
θ
)
P(y,z=1|\theta)
P ( y , z = 1 ∣ θ )
⟶
\qquad \longrightarrow
⟶
z
=
0
z=0
z = 0
A
A
A 反面 ,选择 硬币
C
C
C
y
y
y
P
(
y
,
z
=
0
∣
θ
)
P(y,z=0|\theta)
P ( y , z = 0 ∣ θ )
\qquad
\qquad
隐藏变量
z
z
z
N
N
N
{
y
1
,
y
2
,
⋯
,
y
N
}
,
y
n
∈
{
0
,
1
}
\{ y_{1}, y_{2},\cdots,y_{N}\},\ \ y_{n}\in \{0,1\}
{ y 1 , y 2 , ⋯ , y N } , y n ∈ { 0 , 1 }
{
(
y
1
,
z
1
)
,
(
y
2
,
z
1
)
,
(
y
3
,
z
0
)
,
(
y
4
,
z
1
)
,
(
y
5
,
z
0
)
,
(
y
6
,
z
0
)
,
⋯
,
(
y
N
,
z
1
)
}
\{(y_{1},z_{1}), (y_{2},z_{1}), (y_{3},z_{0}),(y_{4},z_{1}),(y_{5},z_{0}),(y_{6},z_{0}),\cdots,(y_{N},z_{1}) \}
{ ( y 1 , z 1 ) , ( y 2 , z 1 ) , ( y 3 , z 0 ) , ( y 4 , z 1 ) , ( y 5 , z 0 ) , ( y 6 , z 0 ) , ⋯ , ( y N , z 1 ) } 与下文的表示方法不同
z
0
z_{0}
z 0
z
=
0
z=0
z = 0
y
n
y_{n}
y n
z
1
z_{1}
z 1
z
=
1
z=1
z = 1
y
n
y_{n}
y n
采用
1
−
o
f
−
K
1-of-K
1 − o f − K
E
M
EM
E M
\qquad
\qquad
综上所述 :每观测到一枚硬币的投掷结果(
y
=
1
y=1
y = 1
y
=
0
y=0
y = 0
y
y
y
P
(
y
∣
θ
)
P(y|\theta)
P ( y ∣ θ )
P
(
y
∣
θ
)
=
∑
z
∈
{
0
,
1
}
P
(
y
,
z
∣
θ
)
=
∑
z
∈
{
0
,
1
}
P
(
z
∣
θ
)
P
(
y
∣
z
,
θ
)
=
P
(
z
=
1
)
P
(
y
∣
z
=
1
,
θ
)
+
P
(
z
=
0
)
P
(
y
∣
z
=
0
,
θ
)
=
π
⋅
P
(
y
∣
z
=
1
,
θ
)
+
(
1
−
π
)
⋅
P
(
y
∣
z
=
0
,
θ
)
=
π
p
y
(
1
−
p
)
(
1
−
y
)
+
(
1
−
π
)
q
y
(
1
−
q
)
(
1
−
y
)
\qquad\qquad\begin{aligned} P(y|\theta) &= \displaystyle\sum_{z\in\{0,1\}}P(y,z|\theta) \\ &=\displaystyle\sum_{z\in\{0,1\}}P(z|\theta)P(y|z,\theta) \\ &= P(z=1)P(y|z=1,\theta)+P(z=0)P(y|z=0,\theta) \\ &= \pi\cdot P(y|z=1,\theta)+(1- \pi) \cdot P(y|z=0,\theta) \\ &= \pi p^{y}(1-p)^{(1-y)}+(1- \pi)q^{y}(1-q)^{(1-y)} \end{aligned}
P ( y ∣ θ ) = z ∈ { 0 , 1 } ∑ P ( y , z ∣ θ ) = z ∈ { 0 , 1 } ∑ P ( z ∣ θ ) P ( y ∣ z , θ ) = P ( z = 1 ) P ( y ∣ z = 1 , θ ) + P ( z = 0 ) P ( y ∣ z = 0 , θ ) = π ⋅ P ( y ∣ z = 1 , θ ) + ( 1 − π ) ⋅ P ( y ∣ z = 0 , θ ) = π p y ( 1 − p ) ( 1 − y ) + ( 1 − π ) q y ( 1 − q ) ( 1 − y )
\qquad
\qquad
\qquad
N
N
N
(
N
=
10
)
(N=10)
( N = 1 0 )
1
,
1
,
0
,
1
,
0
,
0
,
1
,
0
,
1
,
1
1,1,0,1,0,0,1,0,1,1
1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 观测数据 可以用 随机向量
y
\boldsymbol{y}
y
y
=
{
y
1
,
y
2
,
⋯
,
y
N
}
,
y
n
∈
{
0
,
1
}
\boldsymbol{y} =\{ y_{1}, y_{2},\cdots,y_{N} \},\ \ y_{n}\in \{0,1\}
y = { y 1 , y 2 , ⋯ , y N } , y n ∈ { 0 , 1 } 未观测数据 用随机向量
z
\boldsymbol{z}
z
z
=
{
z
1
,
z
2
,
⋯
,
z
N
}
,
z
n
∈
{
0
,
1
}
\boldsymbol{z} =\{ z_{1}, z_{2},\cdots,z_{N} \},\ \ z_{n}\in \{0,1\}
z = { z 1 , z 2 , ⋯ , z N } , z n ∈ { 0 , 1 }
\qquad
y
=
{
y
1
,
y
2
,
⋯
,
y
N
}
\boldsymbol{y} = \{ y_{1}, y_{2},\cdots,y_{N} \}
y = { y 1 , y 2 , ⋯ , y N } 似然函数
(
l
i
k
e
l
i
h
o
o
d
f
u
n
c
t
i
o
n
)
(likelihood\ function)
( l i k e l i h o o d f u n c t i o n )
P
(
y
∣
θ
)
=
P
(
y
1
,
y
2
,
⋯
,
y
N
∣
θ
)
y
n
∈
{
0
,
1
}
=
∏
n
=
1
N
P
(
y
n
∣
θ
)
=
∏
n
=
1
N
{
∑
z
n
∈
{
0
,
1
}
P
(
y
n
,
z
n
∣
θ
)
}
=
∏
n
=
1
N
{
∑
z
n
∈
{
0
,
1
}
P
(
z
n
∣
θ
)
P
(
y
n
∣
z
n
,
θ
)
}
z
n
∈
{
0
,
1
}
=
∏
n
=
1
N
[
π
p
y
n
(
1
−
p
)
(
1
−
y
n
)
+
(
1
−
π
)
q
y
n
(
1
−
q
)
(
1
−
y
n
)
]
\qquad\qquad\begin{aligned} P(\boldsymbol{y}|\theta) &= P( y_{1}, y_{2},\cdots,y_{N}|\theta)\qquad\qquad\qquad\qquad\ \ \ \ y_{n}\in \{0,1\}\\ &= \prod_{n=1}^{N}P(y_{n}|\theta) \\ &= \prod_{n=1}^{N}\left\{ \displaystyle\sum_{z_{n}\in\{0,1\}}P(y_{n},z_{n}|\theta) \right\} \\ &= \prod_{n=1}^{N}\left\{ \displaystyle\sum_{z_{n}\in\{0,1\}}P(z_{n}|\theta)P( y_{n}|z_{n},\theta)\right\} \qquad\ \ \ z_{n}\in\{0,1\} \\ &= \prod_{n=1}^{N} \left [ \pi p^{y_{n}}(1-p)^{(1-y_{n})}+(1- \pi)q^{y_{n}}(1-q)^{(1-y_{n})} \right] \\ \end{aligned}
P ( y ∣ θ ) = P ( y 1 , y 2 , ⋯ , y N ∣ θ ) y n ∈ { 0 , 1 } = n = 1 ∏ N P ( y n ∣ θ ) = n = 1 ∏ N ⎩ ⎨ ⎧ z n ∈ { 0 , 1 } ∑ P ( y n , z n ∣ θ ) ⎭ ⎬ ⎫ = n = 1 ∏ N ⎩ ⎨ ⎧ z n ∈ { 0 , 1 } ∑ P ( z n ∣ θ ) P ( y n ∣ z n , θ ) ⎭ ⎬ ⎫ z n ∈ { 0 , 1 } = n = 1 ∏ N [ π p y n ( 1 − p ) ( 1 − y n ) + ( 1 − π ) q y n ( 1 − q ) ( 1 − y n ) ]
\qquad
\qquad
\qquad
P
(
y
∣
θ
)
P(\boldsymbol{y}|\theta)
P ( y ∣ θ )
θ
^
=
arg max
θ
P
(
y
∣
θ
)
\hat{\theta} =\argmax_\theta P(\boldsymbol{y}|\theta)
θ ^ = θ a r g m a x P ( y ∣ θ )
θ
^
=
arg max
θ
{
ln
P
(
y
∣
θ
)
}
\hat{\theta} =\argmax_\theta \left\{ \ \ln P(\boldsymbol{y}|\theta)\ \right\}
θ ^ = θ a r g m a x { ln P ( y ∣ θ ) }
\qquad
Revised Figure.1 From《What is the expectation maximization algorithm》H 或 T 的结果都可以明确地写成
(
y
n
,
z
n
)
(y_{n},z_{n})
( y n , z n )
{
(
y
1
=
1
,
z
1
=
1
)
,
(
y
2
=
0
,
z
2
=
0
)
,
⋯
,
(
y
10
=
1
,
z
10
=
1
)
}
\{ (y_{1}=1,z_{1}=1),(y_{2}=0,z_{2}=0),\cdots,(y_{10}=1,z_{10}=1) \}
{ ( y 1 = 1 , z 1 = 1 ) , ( y 2 = 0 , z 2 = 0 ) , ⋯ , ( y 1 0 = 1 , z 1 0 = 1 ) }
π
=
0.5
\pi=0.5
π = 0 . 5
p
=
θ
B
p=\theta_{B}
p = θ B
q
=
θ
C
q=\theta_{C}
q = θ C H表示正面 ,T表示反面 。
θ
B
\theta_{B}
θ B
p
p
p
θ
C
\theta_{C}
θ C
q
q
q
\qquad
θ
^
=
arg max
θ
{
ln
P
(
y
∣
θ
)
}
,
θ
=
(
p
,
q
)
\hat{\theta} =\argmax_\theta \left\{ \ \ln P(\boldsymbol{y}|\theta)\ \right\},\theta=(p,q)
θ ^ = θ a r g m a x { ln P ( y ∣ θ ) } , θ = ( p , q )
\qquad
π
=
1
2
\pi=\dfrac{1}{2}
π = 2 1
P
(
y
∣
θ
)
=
∏
n
=
1
N
[
π
p
y
n
(
1
−
p
)
(
1
−
y
n
)
+
(
1
−
π
)
q
y
n
(
1
−
q
)
(
1
−
y
n
)
]
=
∏
n
=
1
N
[
1
2
p
y
n
(
1
−
p
)
(
1
−
y
n
)
+
1
2
q
y
n
(
1
−
q
)
(
1
−
y
n
)
]
\qquad\qquad\begin{aligned} P(\boldsymbol{y}|\theta) &= \prod_{n=1}^{N} \left [ \pi p^{y_{n}}(1-p)^{(1-y_{n})}+(1- \pi)q^{y_{n}} (1-q)^{(1-y_{n})} \right] \\ &= \prod_{n=1}^{N} \left [ \frac{1}{2} p^{y_{n}}(1-p)^{(1-y_{n})}+\frac{1}{2}q^{y_{n}} (1-q)^{(1-y_{n})} \right]\end{aligned}
P ( y ∣ θ ) = n = 1 ∏ N [ π p y n ( 1 − p ) ( 1 − y n ) + ( 1 − π ) q y n ( 1 − q ) ( 1 − y n ) ] = n = 1 ∏ N [ 2 1 p y n ( 1 − p ) ( 1 − y n ) + 2 1 q y n ( 1 − q ) ( 1 − y n ) ]
\qquad
ln
P
(
y
∣
θ
)
=
∑
n
=
1
N
ln
[
1
2
p
y
n
(
1
−
p
)
(
1
−
y
n
)
+
1
2
q
y
n
(
1
−
q
)
(
1
−
y
n
)
]
=
∑
z
n
=
1
ln
[
1
2
p
y
n
(
1
−
p
)
(
1
−
y
n
)
]
+
∑
z
n
=
0
ln
[
1
2
q
y
n
(
1
−
q
)
(
1
−
y
n
)
]
=
∑
z
n
=
1
[
ln
1
2
+
y
n
ln
p
+
(
1
−
y
n
)
ln
(
1
−
p
)
]
+
∑
z
n
=
0
[
ln
1
2
+
y
n
ln
q
+
(
1
−
y
n
)
ln
(
1
−
q
)
]
=
∑
z
n
=
1
ln
1
2
+
ln
p
⋅
∑
z
n
=
1
y
n
+
ln
(
1
−
p
)
⋅
∑
z
n
=
1
(
1
−
y
n
)
+
∑
z
n
=
0
ln
1
2
+
ln
q
⋅
∑
z
n
=
0
y
n
+
ln
(
1
−
q
)
⋅
∑
z
n
=
0
(
1
−
y
n
)
\qquad\qquad\begin{aligned}\ln P(\boldsymbol{y}|\theta)&=\displaystyle\sum_{n=1}^{N}\ln \left [ \frac{1}{2} p^{y_{n}}(1-p)^{(1-y_{n})}+\frac{1}{2}q^{y_{n}} (1-q)^{(1-y_{n})} \right] \\ &= \displaystyle\sum_{z_{n}=1}\ln\left [ \frac{1}{2} p^{y_{n}}(1-p)^{(1-y_{n})} \right]+ \displaystyle\sum_{z_{n}=0}\ln\left [ \frac{1}{2}q^{y_{n}} (1-q)^{(1-y_{n})} \right] \\ &=\displaystyle\sum_{z_{n}=1}\left [\ln \frac{1}{2} +{y_{n}}\ln p+(1-y_{n})\ln(1-p) \right] +\displaystyle\sum_{z_{n}=0}\left [\ln \frac{1}{2} +{y_{n}}\ln q+(1-y_{n})\ln(1-q) \right] \\ &=\displaystyle\sum_{z_{n}=1}\ln \frac{1}{2} +\ln p \cdot \displaystyle\sum_{z_{n}=1}{y_{n}}+\ln(1-p)\cdot \displaystyle\sum_{z_{n}=1}(1-y_{n}) \\ &\ \ \ \ \ +\displaystyle\sum_{z_{n}=0}\ln \frac{1}{2} +\ln q \cdot \displaystyle\sum_{z_{n}=0}{y_{n}}+\ln(1-q) \cdot \displaystyle\sum_{z_{n}=0}(1-y_{n}) \end{aligned}
ln P ( y ∣ θ ) = n = 1 ∑ N ln [ 2 1 p y n ( 1 − p ) ( 1 − y n ) + 2 1 q y n ( 1 − q ) ( 1 − y n ) ] = z n = 1 ∑ ln [ 2 1 p y n ( 1 − p ) ( 1 − y n ) ] + z n = 0 ∑ ln [ 2 1 q y n ( 1 − q ) ( 1 − y n ) ] = z n = 1 ∑ [ ln 2 1 + y n ln p + ( 1 − y n ) ln ( 1 − p ) ] + z n = 0 ∑ [ ln 2 1 + y n ln q + ( 1 − y n ) ln ( 1 − q ) ] = z n = 1 ∑ ln 2 1 + ln p ⋅ z n = 1 ∑ y n + ln ( 1 − p ) ⋅ z n = 1 ∑ ( 1 − y n ) + z n = 0 ∑ ln 2 1 + ln q ⋅ z n = 0 ∑ y n + ln ( 1 − q ) ⋅ z n = 0 ∑ ( 1 − y n )
\qquad
ln
P
(
y
∣
θ
)
\ln P(\boldsymbol{y}|\theta)
ln P ( y ∣ θ )
p
p
p
q
q
q
∂
ln
P
(
y
∣
θ
)
∂
p
=
∂
{
∑
z
n
=
1
ln
1
2
+
ln
p
⋅
∑
z
n
=
1
y
n
+
ln
(
1
−
p
)
⋅
∑
z
n
=
1
(
1
−
y
n
)
}
∂
p
=
∑
z
n
=
1
y
n
p
−
∑
z
n
=
1
(
1
−
y
n
)
1
−
p
=
0
\qquad\qquad\begin{aligned}\frac{\partial\ln P(\boldsymbol{y}|\theta)}{\partial p}&= \frac{\partial \left\{\sum\limits_{z_{n}=1}\ln \frac{1}{2} +\ln p \cdot \sum\limits_{z_{n}=1}y_{n}+\ln(1-p) \cdot\sum\limits_{z_{n}=1}(1-y_{n})\right\}}{\partial p} \\ &=\frac{\sum\limits_{z_{n}=1}y_{n}}{p}-\frac{\sum\limits_{z_{n}=1}(1-y_{n})}{1-p}=0 \end{aligned}
∂ p ∂ ln P ( y ∣ θ ) = ∂ p ∂ { z n = 1 ∑ ln 2 1 + ln p ⋅ z n = 1 ∑ y n + ln ( 1 − p ) ⋅ z n = 1 ∑ ( 1 − y n ) } = p z n = 1 ∑ y n − 1 − p z n = 1 ∑ ( 1 − y n ) = 0
\qquad\qquad
∂
ln
P
(
y
∣
θ
)
∂
q
=
∂
{
∑
z
n
=
0
ln
1
2
+
ln
q
⋅
∑
z
n
=
0
y
n
+
ln
(
1
−
q
)
⋅
∑
z
n
=
0
(
1
−
y
n
)
}
∂
q
=
∑
z
n
=
0
y
n
q
−
∑
z
n
=
0
(
1
−
y
n
)
1
−
q
=
0
\qquad\qquad\begin{aligned}\frac{\partial\ln P(\boldsymbol{y}|\theta)}{\partial q}&= \frac{\partial \left\{ \sum\limits_{z_{n}=0}\ln \frac{1}{2} +\ln q \cdot \sum\limits_{z_{n}=0}y_{n}+\ln(1-q)\cdot \sum\limits_{z_{n}=0}(1-y_{n})\right\}}{\partial q} \\ &=\frac{\sum\limits_{z_{n}=0}y_{n}}{q}-\frac{\sum\limits_{z_{n}=0}(1-y_{n})}{1-q}=0 \end{aligned}
∂ q ∂ ln P ( y ∣ θ ) = ∂ q ∂ { z n = 0 ∑ ln 2 1 + ln q ⋅ z n = 0 ∑ y n + ln ( 1 − q ) ⋅ z n = 0 ∑ ( 1 − y n ) } = q z n = 0 ∑ y n − 1 − q z n = 0 ∑ ( 1 − y n ) = 0
\qquad
\qquad
p
=
∑
z
n
=
1
y
n
∑
z
n
=
1
y
n
+
∑
z
n
=
1
(
1
−
y
n
)
q
=
∑
z
n
=
0
y
n
∑
z
n
=
0
y
n
+
∑
z
n
=
0
(
1
−
y
n
)
\qquad\qquad\begin{aligned}p&= \frac{\sum\limits_{z_{n}=1}y_{n}}{\sum\limits_{z_{n}=1}y_{n}+\sum\limits_{z_{n}=1}(1-y_{n})} \\ q&= \frac{\sum\limits_{z_{n}=0}y_{n}}{\sum\limits_{z_{n}=0}y_{n}+\sum\limits_{z_{n}=0}(1-y_{n})} \end{aligned}
p q = z n = 1 ∑ y n + z n = 1 ∑ ( 1 − y n ) z n = 1 ∑ y n = z n = 0 ∑ y n + z n = 0 ∑ ( 1 − y n ) z n = 0 ∑ y n
\qquad
\qquad
∑
z
n
=
1
y
n
\sum\limits_{z_{n}=1}{y_{n}}
z n = 1 ∑ y n
(
z
n
=
1
)
(z_{n}=1)
( z n = 1 )
(
y
n
=
1
)
(y_{n}=1)
( y n = 1 )
∑
z
n
=
1
(
1
−
y
n
)
\sum\limits_{z_{n}=1}(1-y_{n})
z n = 1 ∑ ( 1 − y n )
(
y
n
=
0
)
(y_{n}=0)
( y n = 0 )
θ
^
B
=
p
^
=
9
9
+
11
=
0.45
\hat \theta_{B}=\hat p=\frac{9}{9+11}=0.45
θ ^ B = p ^ = 9 + 1 1 9 = 0 . 4 5
∑
z
n
=
0
y
n
\sum\limits_{z_{n}=0}{y_{n}}
z n = 0 ∑ y n
(
z
n
=
0
)
(z_{n}=0)
( z n = 0 )
(
y
n
=
1
)
(y_{n}=1)
( y n = 1 )
∑
z
n
=
0
(
1
−
y
n
)
\sum\limits_{z_{n}=0}(1-y_{n})
z n = 0 ∑ ( 1 − y n )
(
y
n
=
0
)
(y_{n}=0)
( y n = 0 )
θ
^
C
=
q
^
=
24
24
+
6
=
0.80
\hat \theta_{C}=\hat q=\frac{24}{24+6}=0.80
θ ^ C = q ^ = 2 4 + 6 2 4 = 0 . 8 0
\qquad
如果硬币A的投掷过程无法观测 ,即
z
z
z
E
M
EM
E M 迭代的方式 来求取最大似然解。
\qquad
Revised Figure.1 From《What is the expectation maximization algorithm》
\qquad
\qquad
z
z
z 问号表明,我们不知道观测结果到底是用 硬币B 还是 硬币C 投掷出来的),只能观测到 “硬币B 或 硬币C ” 的投掷结果为正面 或反面 。
\qquad
EM 算法的基本思路:
既然有关
Z
=
{
z
1
,
⋯
,
z
N
}
,
z
n
∈
{
0
,
1
}
\bold Z=\{ z_{1},\cdots,z_{N}\},z_{n} \in \{0,1\}
Z = { z 1 , ⋯ , z N } , z n ∈ { 0 , 1 }
Z
\bold Z
Z
(
Y
,
Z
)
(\bold Y, \bold Z)
( Y , Z ) 1.3节那样去进行最大似然估计。
然而,怎么样的猜测 (图中的问号哪些为B、哪些为C,即
Z
\bold Z
Z
(
Y
,
Z
)
(\bold Y, \bold Z)
( Y , Z )
θ
(
i
)
=
(
π
(
i
)
,
p
(
i
)
,
q
(
i
)
)
\theta^{(i)}=(\pi^{(i)},p^{(i)},q^{(i)})
θ ( i ) = ( π ( i ) , p ( i ) , q ( i ) )
E
M
EM
E M
Z
\bold Z
Z
E
P
(
Z
∣
Y
,
θ
)
[
ln
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
E_{P(\bold Z|\bold Y,\theta)}[\ln P(\bold Y, \bold Z|\theta)\ |\ \bold Y,\theta^{(i)}]
E P ( Z ∣ Y , θ ) [ ln P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ]
Z
\bold Z
Z
计算
Q
(
θ
,
θ
(
i
)
)
=
E
P
(
Z
∣
Y
,
θ
)
[
ln
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
Q(\theta,\theta^{(i)})=E_{P(\bold Z|\bold Y,\theta)}[\ln P(\bold Y, \bold Z|\theta)\ |\ \bold Y,\theta^{(i)}]
Q ( θ , θ ( i ) ) = E P ( Z ∣ Y , θ ) [ ln P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] E步。
求使
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q ( θ , θ ( i ) )
θ
\theta
θ
θ
(
i
+
1
)
=
arg max
θ
Q
(
θ
,
θ
(
i
)
)
\theta^{(i+1)}=\argmax_{\theta}\ Q(\theta,\theta^{(i)})
θ ( i + 1 ) = θ a r g m a x Q ( θ , θ ( i ) ) M步。
\qquad
(
1
)
E
\qquad (1)\ E
( 1 ) E
θ
(
i
)
=
(
π
(
i
)
,
p
(
i
)
,
q
(
i
)
)
\theta^{(i)}=(\pi^{(i)},p^{(i)},q^{(i)})
θ ( i ) = ( π ( i ) , p ( i ) , q ( i ) )
\qquad\qquad
y
n
y_{n}
y n
B
B
B
\qquad\qquad\qquad
μ
n
(
i
+
1
)
=
π
(
i
)
(
p
(
i
)
)
y
n
(
1
−
p
(
i
)
)
(
1
−
y
n
)
π
(
i
)
(
p
(
i
)
)
y
n
(
1
−
p
(
i
)
)
(
1
−
y
n
)
+
(
1
−
π
(
i
)
)
(
q
(
i
)
)
y
n
(
1
−
q
(
i
)
)
(
1
−
y
n
)
\mu_{n}^{(i+1)}= \dfrac{\pi^{(i)}(p^{(i)})^{y_{n}}(1-p^{(i)})^{(1-y_{n})}} {\pi^{(i)}(p^{(i)})^{y_{n}}(1-p^{(i)})^{(1-y_{n})}+(1-\pi^{(i)})(q^{(i)})^{y_{n}}(1-q^{(i)})^{(1-y_{n})}}
μ n ( i + 1 ) = π ( i ) ( p ( i ) ) y n ( 1 − p ( i ) ) ( 1 − y n ) + ( 1 − π ( i ) ) ( q ( i ) ) y n ( 1 − q ( i ) ) ( 1 − y n ) π ( i ) ( p ( i ) ) y n ( 1 − p ( i ) ) ( 1 − y n )
\qquad\qquad
y
n
y_{n}
y n
C
C
C
\qquad\qquad\qquad
1
−
μ
n
(
i
+
1
)
=
(
1
−
π
(
i
)
)
(
q
(
i
)
)
y
n
(
1
−
q
(
i
)
)
(
1
−
y
n
)
π
(
i
)
(
p
(
i
)
)
y
n
(
1
−
p
(
i
)
)
(
1
−
y
n
)
+
(
1
−
π
(
i
)
)
(
q
(
i
)
)
y
n
(
1
−
q
(
i
)
)
(
1
−
y
n
)
1-\mu_{n}^{(i+1)}= \dfrac{(1-\pi^{(i)})(q^{(i)})^{y_{n}}(1-q^{(i)})^{(1-y_{n})}} {\pi^{(i)}(p^{(i)})^{y_{n}}(1-p^{(i)})^{(1-y_{n})}+(1-\pi^{(i)})(q^{(i)})^{y_{n}}(1-q^{(i)})^{(1-y_{n})}}
1 − μ n ( i + 1 ) = π ( i ) ( p ( i ) ) y n ( 1 − p ( i ) ) ( 1 − y n ) + ( 1 − π ( i ) ) ( q ( i ) ) y n ( 1 − q ( i ) ) ( 1 − y n ) ( 1 − π ( i ) ) ( q ( i ) ) y n ( 1 − q ( i ) ) ( 1 − y n )
\qquad
(
2
)
M
\qquad (2)\ M
( 2 ) M
θ
(
i
+
1
)
=
(
π
(
i
+
1
)
,
p
(
i
+
1
)
,
q
(
i
+
1
)
)
\theta^{(i+1)}=(\pi^{(i+1)},p^{(i+1)},q^{(i+1)})
θ ( i + 1 ) = ( π ( i + 1 ) , p ( i + 1 ) , q ( i + 1 ) )
π
(
i
+
1
)
=
1
N
∑
n
=
1
N
μ
n
(
i
+
1
)
,
p
(
i
+
1
)
=
∑
n
=
1
N
μ
n
(
i
+
1
)
y
n
∑
n
=
1
N
μ
n
(
i
+
1
)
,
q
(
i
+
1
)
=
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
y
n
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
\qquad\qquad\qquad \pi^{(i+1)} =\frac{1}{N} \displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)}\ ,\ p^{(i+1)} =\frac{\sum\limits_{n=1}^{N} \mu_{n}^{(i+1)}y_{n}}{\sum\limits_{n=1}^{N} \mu_{n}^{(i+1)}} \ , \ q^{(i+1)} =\frac{\sum\limits_{n=1}^{N} (1-\mu_{n}^{(i+1)})y_{n}}{\sum\limits_{n=1}^{N} (1-\mu_{n}^{(i+1)})}
π ( i + 1 ) = N 1 n = 1 ∑ N μ n ( i + 1 ) , p ( i + 1 ) = n = 1 ∑ N μ n ( i + 1 ) n = 1 ∑ N μ n ( i + 1 ) y n , q ( i + 1 ) = n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) y n
\qquad
\qquad
θ
=
(
π
,
p
,
q
)
\theta=(\pi,p,q)
θ = ( π , p , q )
1
)
\qquad1)
1 )
z
1
=
1
z_{1}=1
z 1 = 1 隐藏向量
z
=
[
1
,
0
]
T
\bold z=[1,0]^{T}
z = [ 1 , 0 ] T 事件 “硬币 A 正面 ”
\qquad
P
(
z
1
=
1
∣
θ
)
=
π
P(z_{1}=1|\theta)=\pi
P ( z 1 = 1 ∣ θ ) = π
2
)
\qquad2)
2 )
z
2
=
1
z_{2}=1
z 2 = 1 隐藏向量
z
=
[
0
,
1
]
T
\bold z=[0,1]^{T}
z = [ 0 , 1 ] T 事件 “硬币 A 反面 ”
\qquad
P
(
z
2
=
1
∣
θ
)
=
1
−
π
P(z_{2}=1|\theta)=1-\pi
P ( z 2 = 1 ∣ θ ) = 1 − π
3
)
\qquad3)
3 )
P
(
z
1
=
1
∣
θ
)
=
π
1
=
π
\ P(z_{1}=1|\theta)=\pi_{1}=\pi
P ( z 1 = 1 ∣ θ ) = π 1 = π
\qquad
P
(
z
2
=
1
∣
θ
)
=
π
2
=
1
−
π
\ P(z_{2}=1|\theta)=\pi_{2}=1-\pi
P ( z 2 = 1 ∣ θ ) = π 2 = 1 − π
\qquad
P
(
z
k
=
1
∣
θ
)
=
π
k
,
k
∈
{
1
,
2
}
P(z_{k}=1|\theta)=\pi_{k}\ ,\ \ \ k\in\{1,2\}
P ( z k = 1 ∣ θ ) = π k , k ∈ { 1 , 2 }
\qquad
4
)
\qquad4)
4 )
z
\mathbf z
z
\qquad\qquad
P
(
z
∣
θ
)
=
∏
k
=
1
2
π
k
z
k
=
π
1
z
1
⋅
π
2
z
2
,
z
=
[
z
1
z
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\begin{aligned} P(\mathbf z|\theta) &= \prod_{k=1}^{2} \pi_{k}^{z_{k}} =\pi_{1}^{z_{1}}\cdot\pi_{2}^{z_{2}}\ \ ,\qquad \mathbf z= \left[ \begin{matrix} z_{1}\\z_{2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\} \end{aligned}
P ( z ∣ θ ) = k = 1 ∏ 2 π k z k = π 1 z 1 ⋅ π 2 z 2 , z = [ z 1 z 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
z
\mathbf z
z
y
y
y
1
)
\qquad1)
1 )
y
∈
{
0
,
1
}
y \in \{0,1\}
y ∈ { 0 , 1 }
\qquad
P
(
y
∣
z
1
=
1
,
θ
)
=
p
y
(
1
−
p
)
(
1
−
y
)
P(y|z_{1}=1,\theta)=p^{y}(1-p)^{(1-y)}
P ( y ∣ z 1 = 1 , θ ) = p y ( 1 − p ) ( 1 − y )
\qquad
P
(
y
∣
z
2
=
1
,
θ
)
=
q
y
(
1
−
q
)
(
1
−
y
)
P(y|z_{2}=1,\theta)=q^{y}(1-q)^{(1-y)}
P ( y ∣ z 2 = 1 , θ ) = q y ( 1 − q ) ( 1 − y )
2
)
\qquad2)
2 )
α
1
=
p
\alpha_{1}=p
α 1 = p
α
2
=
q
\alpha_{2}=q
α 2 = q
\qquad
P
(
y
∣
z
1
=
1
,
θ
)
=
p
y
(
1
−
p
)
(
1
−
y
)
=
α
1
y
(
1
−
α
1
)
(
1
−
y
)
P(y|z_{1}=1,\theta)=p^{y}(1-p)^{(1-y)}=\alpha_{1}^{y}(1-\alpha_{1})^{(1-y)}
P ( y ∣ z 1 = 1 , θ ) = p y ( 1 − p ) ( 1 − y ) = α 1 y ( 1 − α 1 ) ( 1 − y )
\qquad
P
(
y
∣
z
2
=
1
,
θ
)
=
q
y
(
1
−
q
)
(
1
−
y
)
=
α
2
y
(
1
−
α
2
)
(
1
−
y
)
P(y|z_{2}=1,\theta)=q^{y}(1-q)^{(1-y)}=\alpha_{2}^{y}(1-\alpha_{2})^{(1-y)}
P ( y ∣ z 2 = 1 , θ ) = q y ( 1 − q ) ( 1 − y ) = α 2 y ( 1 − α 2 ) ( 1 − y )
\qquad
\qquad
\qquad\qquad
P
(
y
∣
z
k
=
1
,
θ
)
=
α
k
y
(
1
−
α
k
)
(
1
−
y
)
,
k
∈
{
1
,
2
}
,
y
∈
{
0
,
1
}
P(y|z_{k}=1,\theta)=\alpha_{k}^{y}(1-\alpha_{k})^{(1-y)},\ \ k \in \{1,2\},\ y \in \{0,1\}
P ( y ∣ z k = 1 , θ ) = α k y ( 1 − α k ) ( 1 − y ) , k ∈ { 1 , 2 } , y ∈ { 0 , 1 }
\qquad
3
)
\qquad3)
3 )
z
\mathbf z
z
\qquad
\qquad\qquad
P
(
y
∣
z
,
θ
)
=
∏
k
=
1
2
[
P
(
y
∣
z
k
=
1
,
θ
)
]
z
k
=
[
P
(
y
∣
z
1
=
1
,
θ
)
]
z
1
⋅
[
P
(
y
∣
z
2
=
1
,
θ
)
]
z
2
=
[
α
1
y
(
1
−
α
1
)
(
1
−
y
)
]
z
1
⋅
[
α
2
y
(
1
−
α
2
)
(
1
−
y
)
]
z
2
=
∏
k
=
1
2
[
α
k
y
(
1
−
α
k
)
(
1
−
y
)
]
z
k
,
z
=
[
z
1
z
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\begin{aligned} P(y|\mathbf z,\theta) &= \prod_{k=1}^{2} \left[\ P(y|z_{k}=1,\theta)\ \right]^{z_{k}} \\ &=\left[P(y|z_{1}=1,\theta)\right]^{z_{1}}\cdot\left[P(y|z_{2}=1,\theta)\right]^{z_{2}} \\ &=\left[\ \alpha_{1}^{y}(1-\alpha_{1})^{(1-y)}\ \right]^{z_{1}}\cdot\left[\ \alpha_{2}^{y}(1-\alpha_{2})^{(1-y)}\ \right]^{z_{2}} \\ &= \prod_{k=1}^{2} \left[\ \alpha_{k}^{y}(1-\alpha_{k})^{(1-y)}\ \right]^{z_{k}},\ \ \ \mathbf z= \left[ \begin{matrix} z_{1}\\z_{2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\} \end{aligned}
P ( y ∣ z , θ ) = k = 1 ∏ 2 [ P ( y ∣ z k = 1 , θ ) ] z k = [ P ( y ∣ z 1 = 1 , θ ) ] z 1 ⋅ [ P ( y ∣ z 2 = 1 , θ ) ] z 2 = [ α 1 y ( 1 − α 1 ) ( 1 − y ) ] z 1 ⋅ [ α 2 y ( 1 − α 2 ) ( 1 − y ) ] z 2 = k = 1 ∏ 2 [ α k y ( 1 − α k ) ( 1 − y ) ] z k , z = [ z 1 z 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
\qquad
\qquad
样本集
Y
=
{
y
1
,
⋯
,
y
N
}
\mathbf Y=\{y_{1},\cdots,y_{N}\}
Y = { y 1 , ⋯ , y N } 隐藏向量集 为
Z
=
{
z
1
,
⋯
,
z
N
}
,
z
n
=
[
z
n
1
z
n
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\mathbf Z=\{ \mathbf z_{1},\cdots,\mathbf z_{N}\},\ \mathbf z_{n}= \left[ \begin{matrix} z_{n1}\\z_{n2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\}
Z = { z 1 , ⋯ , z N } , z n = [ z n 1 z n 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
\qquad\qquad
P
(
Y
∣
Z
,
θ
)
=
P
(
y
1
,
⋯
,
y
N
∣
z
1
,
⋯
,
z
N
,
θ
)
=
∏
n
=
1
N
P
(
y
n
∣
z
n
,
θ
)
由
P
(
y
∣
z
,
θ
)
=
∏
k
=
1
2
[
P
(
y
∣
z
k
=
1
,
θ
)
]
z
k
=
∏
n
=
1
N
∏
k
=
1
2
{
P
(
y
n
∣
z
n
k
=
1
,
θ
)
}
z
n
k
=
∏
n
=
1
N
∏
k
=
1
2
{
α
k
y
n
(
1
−
α
k
)
1
−
y
n
}
z
n
k
\begin{aligned} P(\mathbf Y|\mathbf Z,\theta) &= P(y_{1},\cdots,y_{N}|\mathbf z_{1},\cdots,\mathbf z_{N},\theta) \\ &= \prod_{n=1}^{N} P(y_{n}|\mathbf z_{n},\theta)\qquad\qquad\qquad\ 由 P(y|\mathbf z,\theta) = \prod_{k=1}^{2} \left[\ P(y|z_{k}=1,\theta)\ \right]^{z_{k}} \\ &= \prod_{n=1}^{N}\prod_{k=1}^{2} \left\{\ P(y_{n}|z_{nk}=1,\theta)\ \right\}^{z_{nk}} \\ &= \prod_{n=1}^{N}\prod_{k=1}^{2} \{\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \}^{z_{nk}} \\ \end{aligned}
P ( Y ∣ Z , θ ) = P ( y 1 , ⋯ , y N ∣ z 1 , ⋯ , z N , θ ) = n = 1 ∏ N P ( y n ∣ z n , θ ) 由 P ( y ∣ z , θ ) = k = 1 ∏ 2 [ P ( y ∣ z k = 1 , θ ) ] z k = n = 1 ∏ N k = 1 ∏ 2 { P ( y n ∣ z n k = 1 , θ ) } z n k = n = 1 ∏ N k = 1 ∏ 2 { α k y n ( 1 − α k ) 1 − y n } z n k
\qquad
\qquad\qquad
P
(
z
n
∣
θ
)
=
∏
k
=
1
2
π
k
z
n
k
=
π
1
z
n
1
⋅
π
2
z
n
2
,
z
n
=
[
z
n
1
z
n
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\begin{aligned} P(\mathbf z_{n}|\theta) &= \prod_{k=1}^{2} \pi_{k}^{z_{nk}} =\pi_{1}^{z_{n1}}\cdot\pi_{2}^{z_{n2}}\ \ ,\ \ \ \ \ \mathbf z_{n}= \left[ \begin{matrix} z_{n1}\\z_{n2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\} \end{aligned}
P ( z n ∣ θ ) = k = 1 ∏ 2 π k z n k = π 1 z n 1 ⋅ π 2 z n 2 , z n = [ z n 1 z n 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
\qquad
\qquad\qquad
P
(
Z
∣
θ
)
=
P
(
z
1
,
⋯
,
z
N
∣
θ
)
=
∏
n
=
1
N
P
(
z
n
∣
θ
)
=
∏
n
=
1
N
∏
k
=
1
2
π
k
z
n
k
=
∏
n
=
1
N
π
1
z
n
1
⋅
π
2
z
n
2
,
z
n
=
[
z
n
1
z
n
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\begin{aligned} P(\mathbf Z|\theta) &= P(\mathbf z_{1},\cdots,\mathbf z_{N}|\theta) \\ &=\prod_{n=1}^{N}P(\mathbf z_{n}|\theta) \\ &=\prod_{n=1}^{N}\prod_{k=1}^{2} \pi_{k}^{z_{nk}} \\ &=\prod_{n=1}^{N}\pi_{1}^{z_{n1}}\cdot\pi_{2}^{z_{n2}}\ \ ,\ \ \ \ \ \mathbf z_{n}= \left[ \begin{matrix} z_{n1}\\z_{n2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\} \end{aligned}
P ( Z ∣ θ ) = P ( z 1 , ⋯ , z N ∣ θ ) = n = 1 ∏ N P ( z n ∣ θ ) = n = 1 ∏ N k = 1 ∏ 2 π k z n k = n = 1 ∏ N π 1 z n 1 ⋅ π 2 z n 2 , z n = [ z n 1 z n 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
\qquad
Z
\mathbf Z
Z
E
M
EM
E M 首先对所有的隐藏向量
Z
=
{
z
1
,
⋯
,
z
n
,
⋯
,
z
N
}
\mathbf Z=\{\mathbf z_{1},\cdots,\mathbf z_{n},\cdots,\mathbf z_{N}\}
Z = { z 1 , ⋯ , z n , ⋯ , z N } 进行猜测 ,使得观测数据从 imcomplete 形式 的
Y
\mathbf Y
Y complete 形式 的
(
Y
,
Z
)
(\mathbf Y,\mathbf Z)
( Y , Z )
\qquad
\qquad
(
Y
,
Z
)
(\mathbf Y,\mathbf Z)
( Y , Z ) 似然函数(如果
Z
\mathbf Z
Z
\qquad
\qquad\qquad
P
(
Y
,
Z
∣
θ
)
=
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
=
∏
n
=
1
N
∏
k
=
1
2
{
P
(
y
n
∣
z
n
k
=
1
,
θ
)
}
z
n
k
⋅
∏
n
=
1
N
∏
k
=
1
2
π
k
z
n
k
=
∏
n
=
1
N
∏
k
=
1
2
π
k
z
n
k
{
P
(
y
n
∣
z
n
k
=
1
)
}
z
n
k
=
∏
n
=
1
N
∏
k
=
1
2
π
k
z
n
k
{
α
k
y
n
(
1
−
α
k
)
1
−
y
n
}
z
n
k
\begin{aligned} P(\mathbf Y,\mathbf Z|\theta) &=P(\mathbf Y|\mathbf Z,\theta)P(\mathbf Z|\theta) \\ &=\prod_{n=1}^{N}\prod_{k=1}^{2} \left\{\ P(y_{n}|z_{nk}=1,\theta)\ \right\}^{z_{nk}}\cdot \prod_{n=1}^{N}\prod_{k=1}^{2} \pi_{k}^{z_{nk}} \\ &=\prod_{n=1}^{N}\prod_{k=1}^{2} \pi_{k}^{z_{nk}} \left\{\ P(y_{n}|z_{nk}=1)\ \right\}^{z_{nk}} \\ &=\prod_{n=1}^{N}\prod_{k=1}^{2} \pi_{k}^{z_{nk}} \left\{\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right\}^{z_{nk}} \end{aligned}
P ( Y , Z ∣ θ ) = P ( Y ∣ Z , θ ) P ( Z ∣ θ ) = n = 1 ∏ N k = 1 ∏ 2 { P ( y n ∣ z n k = 1 , θ ) } z n k ⋅ n = 1 ∏ N k = 1 ∏ 2 π k z n k = n = 1 ∏ N k = 1 ∏ 2 π k z n k { P ( y n ∣ z n k = 1 ) } z n k = n = 1 ∏ N k = 1 ∏ 2 π k z n k { α k y n ( 1 − α k ) 1 − y n } z n k
\qquad
对数似然函数(其值取决于
Z
\mathbf Z
Z
\qquad\qquad
ln
P
(
Y
,
Z
∣
θ
)
=
∑
n
=
1
N
∑
k
=
1
2
z
n
k
{
ln
π
k
+
ln
P
(
y
n
∣
z
n
k
=
1
)
}
=
∑
n
=
1
N
∑
k
=
1
2
z
n
k
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
\begin{aligned} \ln P(\mathbf Y,\mathbf Z|\theta) &= \displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} z_{nk} \left\{\ \ln\pi_{k}+\ln P(y_{n}|z_{nk}=1)\ \right\} \\ &= \displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} z_{nk} \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\} \\ \end{aligned}
ln P ( Y , Z ∣ θ ) = n = 1 ∑ N k = 1 ∑ 2 z n k { ln π k + ln P ( y n ∣ z n k = 1 ) } = n = 1 ∑ N k = 1 ∑ 2 z n k { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] }
假设参数
θ
=
(
π
,
α
1
,
α
2
)
\theta=(\pi,\alpha_{1},\alpha_{2})
θ = ( π , α 1 , α 2 )
ln
P
(
Y
,
Z
∣
θ
)
\ln P(\mathbf Y,\mathbf Z|\theta)
ln P ( Y , Z ∣ θ )
Z
=
{
z
1
,
⋯
,
z
n
,
⋯
,
z
N
}
\mathbf Z=\{\mathbf z_{1},\cdots,\mathbf z_{n},\cdots,\mathbf z_{N}\}
Z = { z 1 , ⋯ , z n , ⋯ , z N } 很明确地知道 每一次投掷用的是硬币B还是硬币C,也就是知道所有的
z
n
=
[
1
,
0
]
T
\mathbf z_{n}=[1,0]^{T}
z n = [ 1 , 0 ] T
z
n
=
[
0
,
1
]
T
\mathbf z_{n}=[0,1]^{T}
z n = [ 0 , 1 ] T
ln
P
(
Y
,
Z
∣
θ
)
\ln P(\mathbf Y,\mathbf Z|\theta)
ln P ( Y , Z ∣ θ ) 可以明确计算出 不清楚 每一次投掷用的是硬币B还是硬币C,也就是不知道
z
n
\mathbf z_{n}
z n
[
1
,
0
]
T
[1,0]^{T}
[ 1 , 0 ] T
[
0
,
1
]
T
[0,1]^{T}
[ 0 , 1 ] T
ln
P
(
Y
,
Z
∣
θ
)
\ln P(\mathbf Y,\mathbf Z|\theta)
ln P ( Y , Z ∣ θ ) 无法确定
ln
P
(
Y
,
Z
∣
θ
)
\ln P(\mathbf Y,\mathbf Z|\theta)
ln P ( Y , Z ∣ θ )
\qquad
Z
\mathbf Z
Z
θ
=
(
π
,
α
1
,
α
2
)
\theta=(\pi,\alpha_{1},\alpha_{2})
θ = ( π , α 1 , α 2 )
E
M
EM
E M 对所有的隐藏变量
Z
\mathbf Z
Z
E
Z
[
Z
]
E_{Z}[Z]
E Z [ Z ] :
1
)
\qquad1)
1 )
Y
\mathbf Y
Y
θ
(
i
)
=
(
π
(
i
)
,
p
(
i
)
,
q
(
i
)
)
\theta^{(i)}=(\pi^{(i)},p^{(i)},q^{(i)})
θ ( i ) = ( π ( i ) , p ( i ) , q ( i ) )
Z
\mathbf Z
Z
ln
P
(
Y
,
Z
∣
θ
)
\ln P(\mathbf Y,\mathbf Z|\theta)
ln P ( Y , Z ∣ θ )
2
)
\qquad2)
2 )
Z
\mathbf Z
Z
ln
P
(
Y
,
Z
∣
θ
)
\ln P(\mathbf Y,\mathbf Z|\theta)
ln P ( Y , Z ∣ θ )
\qquad
\qquad\qquad
Q
(
θ
,
θ
(
i
)
)
=
E
P
(
Z
∣
Y
,
θ
)
[
ln
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
=
E
P
(
Z
∣
Y
,
θ
)
{
∑
n
=
1
N
∑
k
=
1
2
z
n
k
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
}
=
∑
n
=
1
N
∑
k
=
1
2
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
\begin{aligned}Q(\theta,\theta^{(i)})&=E_{P(\bold Z|\bold Y,\theta)}[\ln P(\bold Y, \bold Z|\theta)\ |\ \bold Y,\theta^{(i)}] \\ &= E_{P(\bold Z|\bold Y,\theta)}\left\{\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} z_{nk} \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\}\right\} \\ &= \displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\} \\ \end{aligned}
Q ( θ , θ ( i ) ) = E P ( Z ∣ Y , θ ) [ ln P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = E P ( Z ∣ Y , θ ) { n = 1 ∑ N k = 1 ∑ 2 z n k { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] } } = n = 1 ∑ N k = 1 ∑ 2 E P ( Z ∣ Y , θ ) [ z n k ] { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] }
\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]
E P ( Z ∣ Y , θ ) [ z n k ]
z
n
\mathbf z_{n}
z n
\qquad
如果关于
Z
\mathbf Z
Z 已知的,也就是明确知道每一个
z
n
=
[
z
n
1
z
n
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\mathbf z_{n}= \left[ \begin{matrix} z_{n1}\\z_{n2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\}
z n = [ z n 1 z n 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
z
n
k
=
1
z_{nk}=1
z n k = 1
k
k
k 对数似然函数可以写为:
\qquad\qquad
ln
P
(
Y
,
Z
∣
θ
)
=
∑
n
=
1
N
∑
k
=
1
2
z
n
k
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
\ln P(\bold Y, \bold Z|\theta)=\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} z_{nk} \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\}
ln P ( Y , Z ∣ θ ) = n = 1 ∑ N k = 1 ∑ 2 z n k { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] }
\qquad
\qquad
Y
=
{
y
1
,
⋯
,
y
n
,
⋯
,
y
N
}
\bold Y=\{y_{1},\cdots,y_{n},\cdots,y_{N} \}
Y = { y 1 , ⋯ , y n , ⋯ , y N }
y
n
y_{n}
y n
C
1
=
{
n
∣
z
n
1
=
1
}
C_{1}=\{n\ |\ z_{n1}=1\}
C 1 = { n ∣ z n 1 = 1 }
C
2
=
{
n
∣
z
n
2
=
1
}
C_{2}=\{n\ |\ z_{n2}=1\}
C 2 = { n ∣ z n 2 = 1 }
Y
=
C
1
∪
C
2
\bold Y= C_{1} \cup C_{2}
Y = C 1 ∪ C 2
C
1
∩
C
2
=
∅
C_{1} \cap C_{2}=\varnothing
C 1 ∩ C 2 = ∅
\qquad\qquad
ln
P
(
Y
,
Z
∣
θ
)
=
∑
n
=
1
N
∑
k
=
1
2
z
n
k
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
=
∑
n
∈
C
1
z
n
1
{
ln
π
1
+
ln
[
α
1
y
n
(
1
−
α
1
)
1
−
y
n
]
}
+
∑
n
∈
C
2
z
n
2
{
ln
π
2
+
ln
[
α
2
y
n
(
1
−
α
2
)
1
−
y
n
]
}
=
∑
n
∈
C
1
{
ln
π
+
ln
[
p
y
n
(
1
−
p
)
1
−
y
n
]
}
+
∑
n
∈
C
2
{
ln
(
1
−
π
)
+
ln
[
q
y
n
(
1
−
q
)
1
−
y
n
]
}
\begin{aligned}\ln P(\bold Y, \bold Z|\theta)&=\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} z_{nk} \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\}\\ &=\displaystyle\sum_{n\in C_{1}}z_{n1} \left\{\ \ln\pi_{1}+\ln \left[\ \alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\ \right]\ \right\}\\ &\ \ \ +\displaystyle\sum_{n\in C_{2}}z_{n2} \left\{\ \ln\pi_{2}+\ln \left[\ \alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\ \right]\ \right\}\\ &=\displaystyle\sum_{n\in C_{1}} \left\{\ \ln\pi+\ln \left[\ p^{y_{n}}(1-p)^{1-y_{n}}\ \right]\ \right\}\\ &\ \ \ +\displaystyle\sum_{n\in C_{2}} \left\{\ \ln(1-\pi)+\ln \left[\ q^{y_{n}}(1-q)^{1-y_{n}}\ \right]\ \right\}\\ \end{aligned}
ln P ( Y , Z ∣ θ ) = n = 1 ∑ N k = 1 ∑ 2 z n k { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] } = n ∈ C 1 ∑ z n 1 { ln π 1 + ln [ α 1 y n ( 1 − α 1 ) 1 − y n ] } + n ∈ C 2 ∑ z n 2 { ln π 2 + ln [ α 2 y n ( 1 − α 2 ) 1 − y n ] } = n ∈ C 1 ∑ { ln π + ln [ p y n ( 1 − p ) 1 − y n ] } + n ∈ C 2 ∑ { ln ( 1 − π ) + ln [ q y n ( 1 − q ) 1 − y n ] }
\qquad
θ
^
=
(
π
,
p
,
q
)
\hat \theta=(\pi,p,q)
θ ^ = ( π , p , q )
\qquad\qquad
如果关于
Z
\mathbf Z
Z 未知的,所有隐藏变量
z
1
,
⋯
,
z
N
\mathbf z_{1},\cdots,\mathbf z_{N}
z 1 , ⋯ , z N
z
n
k
=
1
z_{nk}=1
z n k = 1
z
n
k
=
0
z_{nk}=0
z n k = 0
\qquad
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q ( θ , θ ( i ) )
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]
E P ( Z ∣ Y , θ ) [ z n k ]
P
(
z
n
∣
y
n
,
θ
(
i
)
)
P(\mathbf z_{n}|y_{n},\theta^{(i)})
P ( z n ∣ y n , θ ( i ) ) 观测数据
y
n
y_{n}
y n 初始值
θ
(
i
)
\theta^{(i)}
θ ( i )
z
n
\mathbf z_{n}
z n
P
(
z
n
1
=
1
∣
y
n
,
θ
)
P(z_{n1}=1|y_{n},\theta)
P ( z n 1 = 1 ∣ y n , θ )
P
(
z
n
2
=
1
∣
y
n
,
θ
)
P(z_{n2}=1|y_{n},\theta)
P ( z n 2 = 1 ∣ y n , θ )
\qquad\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
∑
z
n
k
∈
{
0
,
1
}
z
n
k
P
(
z
n
∣
y
n
,
θ
(
i
)
)
\begin{aligned}E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] &=\displaystyle\sum_{z_{nk}\in\{0,1\}} z_{nk} P(\mathbf z_{n}|y_{n},\theta^{(i)}) \\ \end{aligned}
E P ( Z ∣ Y , θ ) [ z n k ] = z n k ∈ { 0 , 1 } ∑ z n k P ( z n ∣ y n , θ ( i ) )
\qquad\qquad
P
(
z
n
∣
y
n
,
θ
)
=
P
(
y
n
,
z
n
∣
θ
)
P
(
y
n
∣
θ
)
=
P
(
y
n
∣
z
n
,
θ
)
P
(
z
n
∣
θ
)
∑
z
n
P
(
y
n
∣
z
n
,
θ
)
P
(
z
n
∣
θ
)
,
z
n
=
[
z
n
1
z
n
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
=
P
(
y
n
∣
z
n
k
=
1
,
θ
)
P
(
z
n
k
=
1
∣
θ
)
∑
j
=
1
2
P
(
y
n
∣
z
n
j
=
1
,
θ
)
P
(
z
n
j
=
1
∣
θ
)
=
P
(
y
n
∣
z
n
k
=
1
,
θ
)
P
(
z
n
k
=
1
∣
θ
)
P
(
y
n
∣
z
n
1
=
1
,
θ
)
P
(
z
n
1
=
1
∣
θ
)
+
P
(
y
n
∣
z
n
2
=
1
,
θ
)
P
(
z
n
2
=
1
∣
θ
)
=
P
(
y
n
∣
z
n
k
=
1
,
θ
)
P
(
z
n
k
=
1
∣
θ
)
α
1
y
n
(
1
−
α
1
)
1
−
y
n
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
π
2
,
k
∈
{
1
,
2
}
\begin{aligned}P(\mathbf z_{n}|y_{n},\theta) &=\frac{P(y_{n},\mathbf z_{n}|\theta)}{P(y_{n}|\theta)} \\ &=\frac{P(y_{n}|\mathbf z_{n},\theta)P(\mathbf z_{n}|\theta)}{\sum\limits_{\bold z_{n}}P(y_{n}|\mathbf z_{n},\theta)P(\mathbf z_{n}|\theta)}\ ,\qquad\qquad\mathbf z_{n}= \left[ \begin{matrix} z_{n1}\\z_{n2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\}\\ &=\frac{P(y_{n}|z_{nk}=1,\theta)P(z_{nk}=1|\theta)}{\sum\limits_{j=1}^{2}P(y_{n}|z_{nj}=1,\theta)P(z_{nj}=1|\theta)}\ \\ &=\frac{P(y_{n}|z_{nk}=1,\theta)P(z_{nk}=1|\theta)}{P(y_{n}|z_{n1}=1,\theta)P(z_{n1}=1|\theta)+P(y_{n}|z_{n2}=1,\theta)P(z_{n2}=1|\theta)}\ \\ &=\frac{P(y_{n}|z_{nk}=1,\theta)P(z_{nk}=1|\theta)}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}} \pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}} \pi_{2}},\qquad\qquad k\in\{1,2\} \\ \end{aligned}
P ( z n ∣ y n , θ ) = P ( y n ∣ θ ) P ( y n , z n ∣ θ ) = z n ∑ P ( y n ∣ z n , θ ) P ( z n ∣ θ ) P ( y n ∣ z n , θ ) P ( z n ∣ θ ) , z n = [ z n 1 z n 2 ] ∈ { [ 1 0 ] , [ 0 1 ] } = j = 1 ∑ 2 P ( y n ∣ z n j = 1 , θ ) P ( z n j = 1 ∣ θ ) P ( y n ∣ z n k = 1 , θ ) P ( z n k = 1 ∣ θ ) = P ( y n ∣ z n 1 = 1 , θ ) P ( z n 1 = 1 ∣ θ ) + P ( y n ∣ z n 2 = 1 , θ ) P ( z n 2 = 1 ∣ θ ) P ( y n ∣ z n k = 1 , θ ) P ( z n k = 1 ∣ θ ) = α 1 y n ( 1 − α 1 ) 1 − y n π 1 + α 2 y n ( 1 − α 2 ) 1 − y n π 2 P ( y n ∣ z n k = 1 , θ ) P ( z n k = 1 ∣ θ ) , k ∈ { 1 , 2 }
\qquad
\qquad
\qquad
z
n
=
[
z
n
1
z
n
2
]
∈
{
[
1
0
]
,
[
0
1
]
}
\mathbf z_{n}= \left[ \begin{matrix} z_{n1}\\z_{n2} \end{matrix} \right] \in \left\{ \left[ \begin{matrix} 1\\0 \end{matrix} \right],\left[ \begin{matrix} 0\\1 \end{matrix} \right]\right\}
z n = [ z n 1 z n 2 ] ∈ { [ 1 0 ] , [ 0 1 ] }
z
n
k
∈
{
0
,
1
}
z_{nk}\in\{0,1\}
z n k ∈ { 0 , 1 }
\qquad
\qquad\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
∑
z
n
k
∈
{
0
,
1
}
z
n
k
P
(
z
n
∣
y
n
,
θ
(
i
)
)
=
1
⋅
P
(
y
n
∣
z
n
k
=
1
,
θ
(
i
)
)
P
(
z
n
k
=
1
∣
θ
(
i
)
)
+
0
⋅
P
(
y
n
∣
z
n
k
=
0
,
θ
(
i
)
)
P
(
z
n
k
=
0
∣
θ
(
i
)
)
∑
j
=
1
2
P
(
y
n
∣
z
n
j
=
1
,
θ
(
i
)
)
P
(
z
n
j
=
1
∣
θ
(
i
)
)
=
P
(
y
n
∣
z
n
k
=
1
,
θ
(
i
)
)
P
(
z
n
k
=
1
∣
θ
(
i
)
)
α
1
y
n
(
1
−
α
1
)
1
−
y
n
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
π
2
=
∏
k
=
1
2
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
z
n
k
∏
k
=
1
2
π
k
z
n
k
α
1
y
n
(
1
−
α
1
)
1
−
y
n
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
π
2
\begin{aligned}E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] &=\displaystyle\sum_{z_{nk}\in\{0,1\}} z_{nk} P(\mathbf z_{n}|y_{n},\theta^{(i)})\\ &=\frac{1\cdot P(y_{n}|z_{nk}=1,\theta^{(i)})P(z_{nk}=1|\theta^{(i)})+0\cdot P(y_{n}|z_{nk}=0,\theta^{(i)})P(z_{nk}=0|\theta^{(i)})}{\sum\limits_{j=1}^{2}P(y_{n}|z_{nj}=1,\theta^{(i)})P(z_{nj}=1|\theta^{(i)})} \\ &=\frac{P(y_{n}|z_{nk}=1,\theta^{(i)})P(z_{nk}=1|\theta^{(i)})}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}} \pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}} \pi_{2}} \\ &=\frac{\prod_{k=1}^{2}\left[\alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\right]^{z_{nk}} \prod_{k=1}^{2}\pi_{k}^{z_{nk}}}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}} \pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}} \pi_{2}} \\ \end{aligned}
E P ( Z ∣ Y , θ ) [ z n k ] = z n k ∈ { 0 , 1 } ∑ z n k P ( z n ∣ y n , θ ( i ) ) = j = 1 ∑ 2 P ( y n ∣ z n j = 1 , θ ( i ) ) P ( z n j = 1 ∣ θ ( i ) ) 1 ⋅ P ( y n ∣ z n k = 1 , θ ( i ) ) P ( z n k = 1 ∣ θ ( i ) ) + 0 ⋅ P ( y n ∣ z n k = 0 , θ ( i ) ) P ( z n k = 0 ∣ θ ( i ) ) = α 1 y n ( 1 − α 1 ) 1 − y n π 1 + α 2 y n ( 1 − α 2 ) 1 − y n π 2 P ( y n ∣ z n k = 1 , θ ( i ) ) P ( z n k = 1 ∣ θ ( i ) ) = α 1 y n ( 1 − α 1 ) 1 − y n π 1 + α 2 y n ( 1 − α 2 ) 1 − y n π 2 ∏ k = 1 2 [ α k y n ( 1 − α k ) 1 − y n ] z n k ∏ k = 1 2 π k z n k
\qquad
\qquad
ln
P
(
Y
,
Z
∣
θ
)
=
∑
n
=
1
N
∑
k
=
1
2
z
n
k
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
\ln P(\bold Y, \bold Z|\theta) =\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} z_{nk} \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\}
ln P ( Y , Z ∣ θ ) = n = 1 ∑ N k = 1 ∑ 2 z n k { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] } 似然值 的时候,由于
z
n
k
z_{nk}
z n k
θ
(
i
)
\theta^{(i)}
θ ( i )
z
n
k
z_{nk}
z n k
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]
E P ( Z ∣ Y , θ ) [ z n k ]
z
n
k
z_{nk}
z n k
\qquad\qquad
Q
(
θ
,
θ
(
i
)
)
=
∑
n
=
1
N
∑
k
=
1
2
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
\begin{aligned}Q(\theta,\theta^{(i)}) &= \displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\} \\ \end{aligned}
Q ( θ , θ ( i ) ) = n = 1 ∑ N k = 1 ∑ 2 E P ( Z ∣ Y , θ ) [ z n k ] { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] }
\qquad\qquad
其中,
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
P
(
y
n
∣
z
n
k
=
1
,
θ
(
i
)
)
P
(
z
n
k
=
1
∣
θ
(
i
)
)
α
1
y
n
(
1
−
α
1
)
1
−
y
n
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
π
2
E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]=\dfrac{P(y_{n}|z_{nk}=1,\theta^{(i)})P(z_{nk}=1|\theta^{(i)})}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}} \pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}} \pi_{2}}
E P ( Z ∣ Y , θ ) [ z n k ] = α 1 y n ( 1 − α 1 ) 1 − y n π 1 + α 2 y n ( 1 − α 2 ) 1 − y n π 2 P ( y n ∣ z n k = 1 , θ ( i ) ) P ( z n k = 1 ∣ θ ( i ) )
\qquad
E
(
E
x
p
e
c
t
a
t
i
o
n
)
E\ (Expectation)
E ( E x p e c t a t i o n )
\qquad
α
1
=
p
(
i
)
,
α
2
=
q
(
i
)
,
π
1
=
π
(
i
)
,
π
2
=
1
−
π
(
i
)
\alpha_{1}=p^{(i)},\alpha_{2}=q^{(i)},\pi_{1}=\pi^{(i)},\pi_{2}=1-\pi^{(i)}
α 1 = p ( i ) , α 2 = q ( i ) , π 1 = π ( i ) , π 2 = 1 − π ( i )
E
E
E
\qquad\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
∏
k
=
1
2
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
z
n
k
∏
k
=
1
2
π
k
z
n
k
α
1
y
n
(
1
−
α
1
)
1
−
y
n
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
π
2
\begin{aligned}E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] &=\frac{\prod_{k=1}^{2}\left[\alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\right]^{z_{nk}} \prod_{k=1}^{2}\pi_{k}^{z_{nk}}}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}} \pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}} \pi_{2}} \\ \end{aligned}
E P ( Z ∣ Y , θ ) [ z n k ] = α 1 y n ( 1 − α 1 ) 1 − y n π 1 + α 2 y n ( 1 − α 2 ) 1 − y n π 2 ∏ k = 1 2 [ α k y n ( 1 − α k ) 1 − y n ] z n k ∏ k = 1 2 π k z n k
如果观测数据
y
n
y_{n}
y n
B
B
B ,即
z
n
=
[
1
,
0
]
T
\mathbf z_{n}=[1,0]^{T}
z n = [ 1 , 0 ] T
z
n
1
=
1
,
z
n
2
=
0
z_{n1}=1,z_{n2}=0
z n 1 = 1 , z n 2 = 0
\qquad\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
E
P
(
Z
∣
Y
,
θ
)
[
z
n
1
=
1
]
=
α
1
y
n
(
1
−
α
1
)
1
−
y
n
⋅
π
1
α
1
y
n
(
1
−
α
1
)
1
−
y
n
⋅
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
⋅
π
2
=
π
(
i
)
(
p
(
i
)
)
y
n
(
1
−
p
(
i
)
)
1
−
y
n
π
(
i
)
(
p
(
i
)
)
y
n
(
1
−
p
(
i
)
)
1
−
y
n
+
(
1
−
π
(
i
)
)
(
q
(
i
)
)
y
n
(
1
−
q
(
i
)
)
1
−
y
n
\begin{aligned} E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]&= E_{P(\bold Z|\bold Y,\theta)}[z_{n1}=1]\\ &=\frac{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\cdot\pi_{1}}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\cdot\pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\cdot\pi_{2}} \\ &= \frac{\pi^{(i)} (p^{(i)})^{y_{n}}(1-p^{(i)})^{1-y_{n}}}{\pi^{(i)} (p^{(i)})^{y_{n}}(1-p^{(i)})^{1-y_{n}}+(1-\pi^{(i)}) (q^{(i)})^{y_{n}}(1-q^{(i)})^{1-y_{n}}} \\ \end{aligned}
E P ( Z ∣ Y , θ ) [ z n k ] = E P ( Z ∣ Y , θ ) [ z n 1 = 1 ] = α 1 y n ( 1 − α 1 ) 1 − y n ⋅ π 1 + α 2 y n ( 1 − α 2 ) 1 − y n ⋅ π 2 α 1 y n ( 1 − α 1 ) 1 − y n ⋅ π 1 = π ( i ) ( p ( i ) ) y n ( 1 − p ( i ) ) 1 − y n + ( 1 − π ( i ) ) ( q ( i ) ) y n ( 1 − q ( i ) ) 1 − y n π ( i ) ( p ( i ) ) y n ( 1 − p ( i ) ) 1 − y n
如果观测数据
y
n
y_{n}
y n
C
C
C ,即
z
n
=
[
0
,
1
]
T
\mathbf z_{n}=[0,1]^{T}
z n = [ 0 , 1 ] T
z
n
1
=
0
,
z
n
2
=
1
z_{n1}=0,z_{n2}=1
z n 1 = 0 , z n 2 = 1
\qquad\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
E
P
(
Z
∣
Y
,
θ
)
[
z
n
2
=
1
]
=
α
2
y
n
(
1
−
α
2
)
1
−
y
n
⋅
π
2
α
1
y
n
(
1
−
α
1
)
1
−
y
n
⋅
π
1
+
α
2
y
n
(
1
−
α
2
)
1
−
y
n
⋅
π
2
=
(
1
−
π
(
i
)
)
(
q
(
i
)
)
y
n
(
1
−
q
(
i
)
)
1
−
y
n
π
(
i
)
(
p
(
i
)
)
y
n
(
1
−
p
(
i
)
)
1
−
y
n
+
(
1
−
π
(
i
)
)
(
q
(
i
)
)
y
n
(
1
−
q
(
i
)
)
1
−
y
n
\begin{aligned} E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]&= E_{P(\bold Z|\bold Y,\theta)}[z_{n2}=1]\\ &= \frac{\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\cdot\pi_{2}}{\alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\cdot\pi_{1}+\alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\cdot\pi_{2}} \\ &= \frac{(1-\pi^{(i)}) (q^{(i)})^{y_{n}}(1-q^{(i)})^{1-y_{n}}}{\pi^{(i)} (p^{(i)})^{y_{n}}(1-p^{(i)})^{1-y_{n}}+(1-\pi^{(i)}) (q^{(i)})^{y_{n}}(1-q^{(i)})^{1-y_{n}}} \\ \end{aligned}
E P ( Z ∣ Y , θ ) [ z n k ] = E P ( Z ∣ Y , θ ) [ z n 2 = 1 ] = α 1 y n ( 1 − α 1 ) 1 − y n ⋅ π 1 + α 2 y n ( 1 − α 2 ) 1 − y n ⋅ π 2 α 2 y n ( 1 − α 2 ) 1 − y n ⋅ π 2 = π ( i ) ( p ( i ) ) y n ( 1 − p ( i ) ) 1 − y n + ( 1 − π ( i ) ) ( q ( i ) ) y n ( 1 − q ( i ) ) 1 − y n ( 1 − π ( i ) ) ( q ( i ) ) y n ( 1 − q ( i ) ) 1 − y n
\qquad
\qquad
μ
n
(
i
+
1
)
=
E
P
(
Z
∣
Y
,
θ
)
[
z
n
1
=
1
]
\mu_{n}^{(i+1)}=E_{P(\bold Z|\bold Y,\theta)}[z_{n1}=1]
μ n ( i + 1 ) = E P ( Z ∣ Y , θ ) [ z n 1 = 1 ]
E
P
(
Z
∣
Y
,
θ
)
[
z
n
2
=
1
]
=
1
−
μ
n
(
i
+
1
)
E_{P(\bold Z|\bold Y,\theta)}[z_{n2}=1]=1-\mu_{n}^{(i+1)}
E P ( Z ∣ Y , θ ) [ z n 2 = 1 ] = 1 − μ n ( i + 1 )
\qquad
M
(
M
a
x
i
m
i
z
a
t
i
o
n
)
M\ (Maximization)
M ( M a x i m i z a t i o n )
1
)
\qquad1)
1 )
E
E
E
Z
\mathbf Z
Z
θ
(
i
)
\theta^{(i)}
θ ( i ) 似然值
Q
(
θ
,
θ
(
i
)
)
=
E
P
(
Z
∣
Y
,
θ
)
[
ln
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
Q(\theta,\theta^{(i)})=E_{P(\bold Z|\bold Y,\theta)}[\ln P(\bold Y, \bold Z|\theta)\ |\ \bold Y,\theta^{(i)}]
Q ( θ , θ ( i ) ) = E P ( Z ∣ Y , θ ) [ ln P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ]
2
)
\qquad2)
2 )
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]
E P ( Z ∣ Y , θ ) [ z n k ]
z
n
\mathbf z_{n}
z n 估计值,将参数
θ
\theta
θ 未知数,那么就可以对
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q ( θ , θ ( i ) ) 最大似然估计,从而得到新的参数值
θ
(
i
+
1
)
=
(
p
(
i
+
1
)
,
q
(
i
+
1
)
)
\theta^{(i+1)}=(p^{(i+1)},q^{(i+1)})
θ ( i + 1 ) = ( p ( i + 1 ) , q ( i + 1 ) )
M
M
M
\qquad
θ
(
i
+
1
)
=
arg max
θ
Q
(
θ
,
θ
(
i
)
)
\theta^{(i+1)}=\argmax_{\theta} Q(\theta,\theta^{(i)})
θ ( i + 1 ) = θ a r g m a x Q ( θ , θ ( i ) )
3
)
\qquad3)
3 ) 最大似然估计 ,对
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q ( θ , θ ( i ) )
(
α
1
,
α
2
)
(\alpha_{1},\alpha_{2})
( α 1 , α 2 )
(
p
,
q
)
(p,q)
( p , q )
\qquad\qquad
Q
(
θ
,
θ
(
i
)
)
=
∑
n
=
1
N
∑
k
=
1
2
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
=
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
1
]
{
ln
π
1
+
ln
[
α
1
y
n
(
1
−
α
1
)
1
−
y
n
]
}
+
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
2
]
{
ln
π
2
+
ln
[
α
2
y
n
(
1
−
α
2
)
1
−
y
n
]
}
=
∑
n
=
1
N
μ
n
(
i
+
1
)
{
ln
π
1
+
ln
[
α
1
y
n
(
1
−
α
1
)
1
−
y
n
]
}
+
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
{
ln
π
2
+
ln
[
α
2
y
n
(
1
−
α
2
)
1
−
y
n
]
}
\begin{aligned}Q(\theta,\theta^{(i)}) &= \displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\} \\ &=\displaystyle\sum_{n=1}^{N} E_{P(\bold Z|\bold Y,\theta)}[z_{n1}] \left\{\ \ln\pi_{1}+\ln \left[\ \alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\ \right]\ \right\} \\ &\ \ \ +\displaystyle\sum_{n=1}^{N} E_{P(\bold Z|\bold Y,\theta)}[z_{n2}] \left\{\ \ln\pi_{2}+\ln \left[\ \alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\ \right]\ \right\} \\ &=\displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)} \left\{\ \ln\pi_{1}+\ln \left[\ \alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\ \right]\ \right\} \\ &\ \ \ +\displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)}) \left\{\ \ln\pi_{2}+\ln \left[\ \alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\ \right]\ \right\} \\ \end{aligned}
Q ( θ , θ ( i ) ) = n = 1 ∑ N k = 1 ∑ 2 E P ( Z ∣ Y , θ ) [ z n k ] { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] } = n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n 1 ] { ln π 1 + ln [ α 1 y n ( 1 − α 1 ) 1 − y n ] } + n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n 2 ] { ln π 2 + ln [ α 2 y n ( 1 − α 2 ) 1 − y n ] } = n = 1 ∑ N μ n ( i + 1 ) { ln π 1 + ln [ α 1 y n ( 1 − α 1 ) 1 − y n ] } + n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) { ln π 2 + ln [ α 2 y n ( 1 − α 2 ) 1 − y n ] }
\qquad
\qquad
从这里其实可以看出
E
M
EM
E M
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q ( θ , θ ( i ) )
2
2
2 混合 ” ,而
μ
n
(
i
+
1
)
\mu_{n}^{(i+1)}
μ n ( i + 1 )
1
−
μ
n
(
i
+
1
)
1-\mu_{n}^{(i+1)}
1 − μ n ( i + 1 ) 加权系数,即
z
n
\mathbf z_{n}
z n
z
^
n
=
[
z
^
n
1
,
z
^
n
2
]
T
=
[
μ
n
(
i
+
1
)
,
1
−
μ
n
(
i
+
1
)
]
T
\hat \mathbf z_{n}=[\hat z_{n1},\hat z_{n2}]^{T}=[\mu_{n}^{(i+1)},1-\mu_{n}^{(i+1)}]^{T}
z ^ n = [ z ^ n 1 , z ^ n 2 ] T = [ μ n ( i + 1 ) , 1 − μ n ( i + 1 ) ] T
\qquad
p
=
α
1
p=\alpha_{1}
p = α 1
\qquad\qquad
∂
Q
(
θ
,
θ
(
i
)
)
∂
α
1
=
∂
{
∑
n
=
1
N
μ
n
(
i
+
1
)
ln
[
α
1
y
n
(
1
−
α
1
)
1
−
y
n
]
}
∂
α
1
=
∑
n
=
1
N
μ
n
(
i
+
1
)
∂
{
ln
[
α
1
y
n
(
1
−
α
1
)
1
−
y
n
]
}
∂
α
1
=
∑
n
=
1
N
μ
n
(
i
+
1
)
∂
[
y
n
ln
α
1
+
(
1
−
y
n
)
ln
(
1
−
α
1
)
]
∂
α
1
=
∑
n
=
1
N
μ
n
(
i
+
1
)
(
y
n
α
1
−
1
−
y
n
1
−
α
1
)
=
∑
n
=
1
N
μ
n
(
i
+
1
)
y
n
−
α
1
α
1
(
1
−
α
1
)
=
0
\begin{aligned}\frac{\partial Q(\theta,\theta^{(i)})}{\partial \alpha_{1}} &= \dfrac{\partial \left\{ \displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)} \ln \left[\ \alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\ \right] \right\}}{\partial \alpha_{1}}\\ &= \displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)}\dfrac{\partial \left\{ \ln \left[\ \alpha_{1}^{y_{n}}(1-\alpha_{1})^{1-y_{n}}\ \right] \right\}}{\partial \alpha_{1}}\\ &= \displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)}\dfrac{\partial \left[ y_{n} \ln \alpha_{1}+(1-y_{n})\ln(1-\alpha_{1})\ \right]}{\partial \alpha_{1}}\\ &= \displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)}\left(\dfrac{ y_{n}}{ \alpha_{1}}-\dfrac{1-y_{n}}{1-\alpha_{1}}\right)\\ &= \displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)}\dfrac{ y_{n}-\alpha_{1}}{ \alpha_{1}(1-\alpha_{1})}=0\\ \end{aligned}
∂ α 1 ∂ Q ( θ , θ ( i ) ) = ∂ α 1 ∂ { n = 1 ∑ N μ n ( i + 1 ) ln [ α 1 y n ( 1 − α 1 ) 1 − y n ] } = n = 1 ∑ N μ n ( i + 1 ) ∂ α 1 ∂ { ln [ α 1 y n ( 1 − α 1 ) 1 − y n ] } = n = 1 ∑ N μ n ( i + 1 ) ∂ α 1 ∂ [ y n ln α 1 + ( 1 − y n ) ln ( 1 − α 1 ) ] = n = 1 ∑ N μ n ( i + 1 ) ( α 1 y n − 1 − α 1 1 − y n ) = n = 1 ∑ N μ n ( i + 1 ) α 1 ( 1 − α 1 ) y n − α 1 = 0
\qquad\qquad
∑
n
=
1
N
μ
n
(
i
+
1
)
y
n
=
α
1
∑
n
=
1
N
μ
n
(
i
+
1
)
\displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)} y_{n} = \alpha_{1}\displaystyle\sum_{n=1}^{N}\mu_{n}^{(i+1)}
n = 1 ∑ N μ n ( i + 1 ) y n = α 1 n = 1 ∑ N μ n ( i + 1 )
\qquad\qquad
p
(
i
+
1
)
=
α
1
(
i
+
1
)
=
∑
n
=
1
N
μ
n
(
i
+
1
)
y
n
∑
n
=
1
N
μ
n
(
i
+
1
)
p^{(i+1)}=\alpha_{1}^{(i+1)} = \frac{\displaystyle\sum_{n=1}^{N} \mu_{n}^{(i+1)} y_{n}}{\displaystyle\sum_{n=1}^{N}\mu_{n}^{(i+1)}}
p ( i + 1 ) = α 1 ( i + 1 ) = n = 1 ∑ N μ n ( i + 1 ) n = 1 ∑ N μ n ( i + 1 ) y n
\qquad
\qquad
q
=
α
2
q=\alpha_{2}
q = α 2
\qquad\qquad
∂
Q
(
θ
,
θ
(
i
)
)
∂
α
2
=
∂
{
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
ln
[
α
2
y
n
(
1
−
α
2
)
1
−
y
n
]
}
∂
α
2
=
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
∂
{
ln
[
α
2
y
n
(
1
−
α
2
)
1
−
y
n
]
}
∂
α
2
=
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
∂
[
y
n
ln
α
2
+
(
1
−
y
n
)
ln
(
1
−
α
2
)
]
∂
α
2
=
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
(
y
n
α
2
−
1
−
y
n
1
−
α
2
)
=
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
y
n
−
α
2
α
2
(
1
−
α
2
)
=
0
\begin{aligned}\frac{\partial Q(\theta,\theta^{(i)})}{\partial \alpha_{2}} &= \dfrac{\partial \left\{ \displaystyle\sum_{n=1}^{N} (1-\mu_{n}^{(i+1)}) \ln \left[\ \alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\ \right] \right\}}{\partial \alpha_{2}}\\ &= \displaystyle\sum_{n=1}^{N} (1-\mu_{n}^{(i+1)})\dfrac{\partial \left\{ \ln \left[\ \alpha_{2}^{y_{n}}(1-\alpha_{2})^{1-y_{n}}\ \right] \right\}}{\partial \alpha_{2}}\\ &= \displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)})\dfrac{\partial \left[ y_{n} \ln \alpha_{2}+(1-y_{n})\ln(1-\alpha_{2})\ \right]}{\partial \alpha_{2}}\\ &= \displaystyle\sum_{n=1}^{N} (1-\mu_{n}^{(i+1)})\left(\dfrac{ y_{n}}{ \alpha_{2}}-\dfrac{1-y_{n}}{1-\alpha_{2}}\right)\\ &= \displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)})\dfrac{ y_{n}-\alpha_{2}}{ \alpha_{2}(1-\alpha_{2})}=0\\ \end{aligned}
∂ α 2 ∂ Q ( θ , θ ( i ) ) = ∂ α 2 ∂ { n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) ln [ α 2 y n ( 1 − α 2 ) 1 − y n ] } = n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) ∂ α 2 ∂ { ln [ α 2 y n ( 1 − α 2 ) 1 − y n ] } = n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) ∂ α 2 ∂ [ y n ln α 2 + ( 1 − y n ) ln ( 1 − α 2 ) ] = n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) ( α 2 y n − 1 − α 2 1 − y n ) = n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) α 2 ( 1 − α 2 ) y n − α 2 = 0
\qquad\qquad
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
y
n
=
α
2
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
\displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)})y_{n} = \alpha_{2}\displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)})
n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) y n = α 2 n = 1 ∑ N ( 1 − μ n ( i + 1 ) )
\qquad\qquad
q
(
i
+
1
)
=
α
2
(
i
+
1
)
=
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
y
n
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
q^{(i+1)}=\alpha_{2}^{(i+1)} = \frac{\displaystyle\sum_{n=1}^{N} (1-\mu_{n}^{(i+1)}) y_{n}}{\displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)})}
q ( i + 1 ) = α 2 ( i + 1 ) = n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) n = 1 ∑ N ( 1 − μ n ( i + 1 ) ) y n
\qquad
\qquad
π
1
=
π
,
π
2
=
1
−
π
\pi_{1}=\pi,\pi_{2}=1-\pi
π 1 = π , π 2 = 1 − π
Q
(
θ
,
θ
(
i
)
)
=
E
P
(
Z
∣
Y
,
θ
)
[
ln
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
Q(\theta,\theta^{(i)})=E_{P(\bold Z|\bold Y,\theta)}[\ln P(\bold Y, \bold Z|\theta)\ |\ \bold Y,\theta^{(i)}]
Q ( θ , θ ( i ) ) = E P ( Z ∣ Y , θ ) [ ln P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ]
∑
k
π
k
=
1
\sum\limits_{k}\pi_{k}=1
k ∑ π k = 1
\qquad\qquad
max
{
∑
n
=
1
N
∑
k
=
1
2
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
{
ln
π
k
+
ln
[
α
k
y
n
(
1
−
α
k
)
1
−
y
n
]
}
+
λ
(
∑
k
π
k
−
1
)
}
\max\ \left\{ \displaystyle\sum_{n=1}^{N}\displaystyle\sum_{k=1}^{2} E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] \left\{\ \ln\pi_{k}+\ln \left[\ \alpha_{k}^{y_{n}}(1-\alpha_{k})^{1-y_{n}}\ \right]\ \right\} +\lambda(\sum\limits_{k}\pi_{k}-1) \right\}
max { n = 1 ∑ N k = 1 ∑ 2 E P ( Z ∣ Y , θ ) [ z n k ] { ln π k + ln [ α k y n ( 1 − α k ) 1 − y n ] } + λ ( k ∑ π k − 1 ) }
\qquad\qquad
π
k
\pi_{k}
π k
\qquad\qquad\qquad
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
π
k
+
λ
=
0
\displaystyle\sum_{n=1}^{N}\frac{E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]}{\pi_{k}} +\lambda=0
n = 1 ∑ N π k E P ( Z ∣ Y , θ ) [ z n k ] + λ = 0
\qquad\qquad
π
k
\pi_{k}
π k
\qquad\qquad\qquad
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
+
π
k
λ
=
0
\displaystyle\sum_{n=1}^{N}E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] +\pi_{k}\lambda=0
n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n k ] + π k λ = 0
\qquad\qquad
π
k
\pi_{k}
π k
\qquad\qquad\qquad
∑
k
=
1
K
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
+
∑
k
=
1
K
π
k
λ
=
0
\displaystyle\sum_{k=1}^{K}\displaystyle\sum_{n=1}^{N}E_{P(\bold Z|\bold Y,\theta)}[z_{nk}] +\displaystyle\sum_{k=1}^{K}\pi_{k}\lambda=0
k = 1 ∑ K n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n k ] + k = 1 ∑ K π k λ = 0
\qquad\qquad
\qquad\qquad\qquad
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
P
(
y
n
∣
z
n
k
=
1
,
θ
)
P
(
z
n
k
=
1
∣
θ
)
∑
j
=
1
K
P
(
y
n
∣
z
n
j
=
1
,
θ
)
P
(
z
n
j
=
1
∣
θ
)
E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]=\dfrac{P(y_{n}|z_{nk}=1,\theta)P(z_{nk}=1|\theta)}{\sum\limits_{j=1}^{K}P(y_{n}|z_{nj}=1,\theta)P(z_{nj}=1|\theta)}
E P ( Z ∣ Y , θ ) [ z n k ] = j = 1 ∑ K P ( y n ∣ z n j = 1 , θ ) P ( z n j = 1 ∣ θ ) P ( y n ∣ z n k = 1 , θ ) P ( z n k = 1 ∣ θ )
K
=
2
K=2
K = 2
\qquad\qquad
\qquad\qquad\qquad
∑
k
=
1
K
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
k
]
=
∑
k
=
1
K
∑
n
=
1
N
P
(
y
n
∣
z
n
k
=
1
,
θ
)
P
(
z
n
k
=
1
∣
θ
)
∑
j
=
1
K
P
(
y
n
∣
z
n
j
=
1
,
θ
)
P
(
z
n
j
=
1
∣
θ
)
=
∑
n
=
1
N
∑
k
=
1
K
P
(
y
n
∣
z
n
k
=
1
,
θ
)
P
(
z
n
k
=
1
∣
θ
)
∑
j
=
1
K
P
(
y
n
∣
z
n
j
=
1
,
θ
)
P
(
z
n
j
=
1
∣
θ
)
=
N
\begin{aligned}\displaystyle\sum_{k=1}^{K}\displaystyle\sum_{n=1}^{N}E_{P(\bold Z|\bold Y,\theta)}[z_{nk}]&=\displaystyle\sum_{k=1}^{K}\displaystyle\sum_{n=1}^{N}\dfrac{P(y_{n}|z_{nk}=1,\theta)P(z_{nk}=1|\theta)}{\sum\limits_{j=1}^{K}P(y_{n}|z_{nj}=1,\theta)P(z_{nj}=1|\theta)}\\ &=\dfrac{\sum\limits_{n=1}^{N}\sum\limits_{k=1}^{K}P(y_{n}|z_{nk}=1,\theta)P(z_{nk}=1|\theta)}{\sum\limits_{j=1}^{K}P(y_{n}|z_{nj}=1,\theta)P(z_{nj}=1|\theta)} \\ &=N\\ \end{aligned}
k = 1 ∑ K n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n k ] = k = 1 ∑ K n = 1 ∑ N j = 1 ∑ K P ( y n ∣ z n j = 1 , θ ) P ( z n j = 1 ∣ θ ) P ( y n ∣ z n k = 1 , θ ) P ( z n k = 1 ∣ θ ) = j = 1 ∑ K P ( y n ∣ z n j = 1 , θ ) P ( z n j = 1 ∣ θ ) n = 1 ∑ N k = 1 ∑ K P ( y n ∣ z n k = 1 , θ ) P ( z n k = 1 ∣ θ ) = N
\qquad\qquad
λ
=
−
N
\lambda=-N
λ = − N
\qquad\qquad
π
1
=
1
N
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
1
]
=
1
N
∑
n
=
1
N
μ
n
(
i
+
1
)
\pi_{1}=\dfrac{1}{N}\displaystyle\sum_{n=1}^{N}E_{P(\bold Z|\bold Y,\theta)}[z_{n1}]=\dfrac{1}{N}\displaystyle\sum_{n=1}^{N}\mu_{n}^{(i+1)}
π 1 = N 1 n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n 1 ] = N 1 n = 1 ∑ N μ n ( i + 1 )
\qquad\qquad
π
2
=
1
N
∑
n
=
1
N
E
P
(
Z
∣
Y
,
θ
)
[
z
n
2
]
=
1
N
∑
n
=
1
N
(
1
−
μ
n
(
i
+
1
)
)
\pi_{2}=\dfrac{1}{N}\displaystyle\sum_{n=1}^{N}E_{P(\bold Z|\bold Y,\theta)}[z_{n2}]=\dfrac{1}{N}\displaystyle\sum_{n=1}^{N}(1-\mu_{n}^{(i+1)})
π 2 = N 1 n = 1 ∑ N E P ( Z ∣ Y , θ ) [ z n 2 ] = N 1 n = 1 ∑ N ( 1 − μ n ( i + 1 ) )
\qquad\qquad
π
(
i
+
1
)
=
π
1
(
i
+
1
)
=
1
N
∑
n
=
1
N
μ
n
(
i
+
1
)
\pi^{(i+1)}=\pi_{1}^{(i+1)}=\dfrac{1}{N}\displaystyle\sum_{n=1}^{N}\mu_{n}^{(i+1)}
π ( i + 1 ) = π 1 ( i + 1 ) = N 1 n = 1 ∑ N μ n ( i + 1 )
\qquad
\qquad
三硬币问题 与混合高斯模型 本质上是一样的:
混合高斯模型 是“
K
K
K
p
(
x
∣
π
,
μ
,
Σ
)
=
∑
k
=
1
K
π
k
N
(
x
∣
μ
k
,
Σ
k
)
,
∑
k
=
1
K
π
k
=
1
\qquad\qquad p(\mathbf{x}|\boldsymbol{\pi},\boldsymbol{\mu},\boldsymbol{\Sigma})=\displaystyle\sum_{k=1}^{K}\pi_{k}\mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_{k},\boldsymbol{\Sigma}_{k})\ \ ,\qquad\displaystyle\sum_{k=1}^{K}\pi_{k}=1
p ( x ∣ π , μ , Σ ) = k = 1 ∑ K π k N ( x ∣ μ k , Σ k ) , k = 1 ∑ K π k = 1 三硬币问题 实际上是“
2
2
2
P
(
y
∣
π
,
α
)
=
∑
k
=
1
2
π
k
P
(
y
∣
α
k
)
,
∑
k
=
1
2
π
k
=
1
,
P
(
y
∣
α
k
)
=
α
k
y
(
1
−
α
k
)
(
1
−
y
)
\qquad\qquad\begin{aligned} P(y|\boldsymbol{\pi},\boldsymbol{\alpha}) &= \displaystyle\sum_{k=1}^{2}\pi_{k}P(y|\alpha_{k})\ \ ,\ \displaystyle\sum_{k=1}^{2}\pi_{k}=1,\ P(y|\alpha_{k})=\alpha_{k}^{y}(1-\alpha_{k})^{(1-y)} \end{aligned}
P ( y ∣ π , α ) = k = 1 ∑ 2 π k P ( y ∣ α k ) , k = 1 ∑ 2 π k = 1 , P ( y ∣ α k ) = α k y ( 1 − α k ) ( 1 − y )
\qquad
代码:(李航《统计学习方法》9.1.1)
import numpy as np
y = np. array( [ 1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 ] )
N = len ( y)
pi_n = 0.4
p_n = 0.6
q_n = 0.7
flag = 1
iter = 0
while flag:
pi = pi_n
p = p_n
q = q_n
mu = np. zeros( N)
i = 0
for n in y:
t1 = pi* np. power( p, n) * np. power( 1 - p, 1 - n)
t2 = ( 1 - pi) * np. power( q, n) * np. power( 1 - q, 1 - n)
mu[ i] = t1/ ( t1+ t2)
i = i + 1
pi_n = np. sum ( mu) / N
p_n = np. sum ( y* mu) / np. sum ( mu)
q_n = np. sum ( y* ( 1 - mu) ) / np. sum ( 1 - mu)
print ( ( '%1.4f %5.4f %5.4f' ) % ( pi_n, p_n, q_n) )
iter = iter + 1
if iter == 2 :
flag = 0