一道数学题加强版[from CommonAnts][拉格朗日插值][高阶差分]

题目

LOJ
TiwNB
$f(k,x)=\begin{cases} 1&(x=1)\\ \sum_{i=1}^{x-1}f(k,i)+x^k&(x>1) \end{cases}$
求 $f(k,n)$
$n\le 10^{10^6}$

分析

什么神仙玩意…
首先可以推导 $f(k,x)$ 的通项公式

$f(k,x)=\sum_{i=1}^{x-1}f(k,i)+x^k$
$f(k,x-1)=\sum_{i=1}^{x-2}f(k,i)+(x-1)^k$
$f(k,x)-f(k,x-1)=x^k+f(k,x-1)-(x-1)^k$
$f(k,x)=2*f(k,x-1)+x^k-(x-1)^k$
找规律可得：
$f(k,n)=n^k+\sum_{i=0}^{n-1}2^{n-i-1}i^k=n^k+2^{n-1}\sum_{i=0}^{n-1}\frac{i^k}{2^i}$
记 $a=\frac{1}{2}$
$F_k(n)=\sum_{i=0}^{n-1}a^ii^k$
然后发现其满足 $F_k(n)=a^nG_k(n)-G_k(0),G_k(n)$ 为关于 $n$ 的 $k$ 次多项式
推导可以看 $Tiw$ 的博客
然后利用什么差分公式,将 $G_k(n)$ 全部用 $G_k(n)=aG_k(0)+b$ 的形式表示带入求解，特殊地 $G_k(0)=1G_k(0)+0$

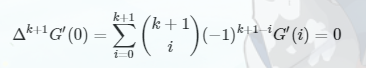
然后求解出 $G_k(n)$ 的前 $k+1$ 项进行拉格朗日插值然后算第 $n$ 项
注意有 $n$ 很大时候取模底数模 $Mod$ 指数模 $Mod-1$
TiwNB

代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<set>    
#include<map>    
#include<stack>    
#include<ctime>    
#include<cstdio>    
#include<queue>    
#include<cmath>    
#include<vector>    
#include<cstring>   
#include<climits>    
#include<iostream>   
#include<algorithm>
using namespace std;
#define LL long long
int read(){
    int f=1,x=0;char c=getchar();
    while(c<'0'||'9'<c){if(c=='-')f=-1;c=getchar();}
    while('0'<=c&&c<='9'){x=x*10+c-'0';c=getchar();}
    return f*x;
}
#define INF 0x3f3f3f3f
#define MAXN 1000005
#define inv2 500000004
#define Mod (int)(1e9+7)
inline int Mul(register LL x,int y){x*=y;return x>=Mod?x%Mod:x;}
inline int Add(int x,int y){x+=y;return x>=Mod?x-Mod:x;}
inline int Sub(int x,int y){x-=y;return x<0?x+Mod:x;}
int Pow(int x,LL y){
	int ret=1;
	while(y){
		if(y&1) ret=Mul(ret,x);
		x=Mul(x,x);
		y>>=1;
	}
	return ret;
}
int p2[MAXN+5],ip2[MAXN+5];
int fac[MAXN+5],ifac[MAXN+5],inv[MAXN+5];
int C(int n,int m){return 1ll*fac[n]*ifac[m]%Mod*ifac[n-m]%Mod;}
void Init(){
	fac[0]=1,p2[0]=ip2[0]=1;
	for(int i=1;i<=MAXN;i++)
		p2[i]=Add(p2[i-1],p2[i-1]),ip2[i]=1ll*ip2[i-1]*inv2%Mod;
	for(int i=1;i<=MAXN;i++)
		fac[i]=1ll*fac[i-1]*i%Mod; 
	ifac[MAXN]=Pow(fac[MAXN],Mod-2);
	for(int i=MAXN-1;i>=0;i--)
		ifac[i]=Mul(ifac[i+1],i+1);
	inv[1]=1;
	for(int i=2;i<=MAXN;i++)
		inv[i]=1ll*(Mod-Mod/i)*inv[Mod%i]%Mod;
	return ;
}
int n,p,k;
char str[MAXN+5];
void Read(){
	scanf("%s",str+1);
	int len=strlen(str+1);
	for(int i=1;i<=len;i++)
		n=(n*10ll+(str[i]^48))%Mod,p=(p*10ll+(str[i]^48))%(Mod-1);
	k=read();
	return ;
}
int g[MAXN+5],L[MAXN+5],R[MAXN+5];
int Lagrange(int x,int K){
	L[0]=1,R[K+1]=1;
	for(int i=1;i<=K;i++)
		L[i]=Mul(L[i-1],Sub(x,i));
	for(int i=K;i>=1;i--)
		R[i]=Mul(R[i+1],Sub(x,i));
	int ret=0;
	for(int i=1;i<=K;i++){
		int tmp=Mul(Mul(L[i-1],R[i+1]),Mul(ifac[i-1],ifac[K-i]));
		if((K-i)&1)
			ret=Sub(ret,Mul(tmp,g[i]));
		else ret=Add(ret,Mul(tmp,g[i]));
	}
	return ret;
}
int xa[MAXN+5],xb[MAXN+5];
int main(){
	Init();
	Read();
	int sf=0;
	xa[0]=1;
	for(int i=1;i<=k+1;i++){
		xa[i]=p2[i],xb[i]=Mul(sf,p2[i]);
		sf=Add(sf,Mul(ip2[i],Pow(i,k)));
	}
	int A=0,B=0;
	for(int i=0;i<=k+1;i++){
		int num=C(k+1,i);
		if((k+1-i)&1)
			A=Sub(A,Mul(num,xa[i])),B=Sub(B,Mul(num,xb[i]));
		else A=Add(A,Mul(num,xa[i])),B=Add(B,Mul(num,xb[i]));
	}
	g[0]=Mul(Pow(A,Mod-2),Mod-B);
	for(int i=1;i<=k+1;i++)
		g[i]=Add(Mul(xa[i],g[0]),xb[i]);
	int ans=Sub(Mul(Pow(inv2,p),Lagrange(n,k+1)),g[0]);
	printf("%d\n",Add(Pow(n,k),Mul(Pow(2,p-1),ans)));
	return 0;
}