判断两个数之间的素数

素数，指在大于1的自然数中，除了1和该数自身外，无法被其他自然数整除的数。大于1的自然数若不是素数，则称之为合数。
很自然通过定义我们就可以得到如何判断一个数是否是素数的算法
（python）

n=int(input())
isprime=1
for i in range(2,n):
    if n%i==0:
        isprime=0
        break
if isprime==1:
    print('Yes')
else:
    print('No')

在这里我们用1来表示素数，0表示非素数（即合数）。
（c语言）

#include <stdio.h>
int main()
{
   int n,i;
   scanf("%d",&n);
   int isprime=1;
   for (i=2;i<n;i++){
       if (n%i==0){
           isprime=1;
           break;
        }
}
   printf("%d",isprime);
   
   return 0;
}

现在我们知道了判断某一个数是否是素数的方法，那给你一串数该怎么判断呢，显然一个一个判断就行。
（python）
给定两个正整数m,n，输出区间[m,n]内的所有素数。

m,n=map(int,input().split())
isprime=1
for i in range(m,n+1):
    for j in range(2,i):
        if i%j==0:
            isprime=0
            break
    else:
        print(i) #输出所有的素数

这里使用了一个for-else语句，使代码看起来更简洁。为了遍历m和n之间的所有的数，使用了双重for循环。
（c语言）

#include <stdio.h>
int main()
{
    int M,N;
    int x;
    scanf("%d %d",&M,&N);

    for (x=M;x<N+1;x++){
        int i=2;
        int isprime=1;
        for (i=2;i<x;i++){
            if (x%i==0){ 
            isprime=0;
            break;}  //只要有比1大的因子，就一定不是素数，终止循环
        }
        if (isprime==1){
        printf("%d ",x);}
    }

    return 0;
}

现在我们已经知道如何简单的输出一定范围内的素数了，更进一步，你能不能输出前100个素数，以及第m个到第n个素数这些问题。
用python我们来做一个素数表，在这个表里的数都是素数。

n=int(input())
a=[i for i in range(2,n+1)]
b=[]
for i in range(len(a)):
    for j in range(2,a[i]):
        if a[i]%j==0 and a[i]!=2:
            break
    else:
        b.append(a[i])
print(b)

使用列表我们可以找出从1到n的素数，n取到很大时，就做出了一张很大的质数表，可以筛除那些合数。

a=[i for i in range(2,10000)]
b=[]
for i in range(len(a)):
    for j in range(2,a[i]):
        if a[i]%j==0 and a[i]!=2:
            break
    else:
        b.append(a[i])
m,n=map(int,input().split())
print(b[m-1:n])

在上面的代码里，我们先筛出了10000以内的素数，之后只需要在列表b里面找素数就可以了，如上就可以找出第m个素数到第n个素数。

显然先建一个列表这种方法很费力气，只是无聊的时候可以这样玩玩。

对于一般问题，我们已经可以成功解决了，但是有时候给我们的数据范围很大，这就要求我们得一定程度上优化算法。
（1）开平方法

如果大于1的整数a不能被所有不超过根号a的素数整除，那么a一定是素数。

n=int(input())
isprime=1
k=int(n**0.5)+1
for i in range(2,k):
    if n%i==0:
        isprime=0
        break
if isprime==1:
    print("Yes")
else:
    print('No')

不难得到原来的程序时间复杂度是 $O (n),$现在优化到了 $O(\sqrt{n})$。c语言代码类似，此处不再赘述。
（2）素数和6的关系

（大于等于5的）质数一定和6的倍数相邻，一定是6x-1或6x-1。利用这种特性。可以对整数进行筛选，只判断那些是6x-1或6x-1的整数是否为质数。

令x≥1，将大于等于5的自然数表示如下： ······6x-1，6x，6x+1，6x+2，6x+3，6x+4······（相邻6个数为一组）
在以上的数字中，6x、6x+2和6x+4是偶数，一定不是质数；6x+3可以分解为3(2x+1)，不是质数，因此质数只能是6x-1和6x+1。

由以上结论，可以得出更简洁的代码。

n=int(input())     #n是大于等于5的正整数
isprime=1
k=int(n**0.5)+1
if n%6==1 or n%6==5:
    for i in range(2,k):
        if n%i==0:
            isprime=0
            break
    if isprime==1:
        print("Yes")
else:
    print('No')

时间复杂度由 $O(\sqrt{n})$降到了原来的三分之一，因为我们只需要从三分之一的数里面来找素数，但时间复杂度只是在常数上做变化，n相当大时没有很大的贡献，类似于开平方法。

单个数的判断基本上已经定型了，但对于求1到n之间的所有素数，我们还有一些方法。
（3）埃氏筛法
已知2是素数，那么2的倍数一定是合数，3是素数，3的倍数也是合数。当知道某个数是素数之后，它的倍数就可以去掉了。这样后面要筛的数就会越来越少，比如2的倍数就可以去掉一半的数，三的倍数可以去掉1/3的数等等。

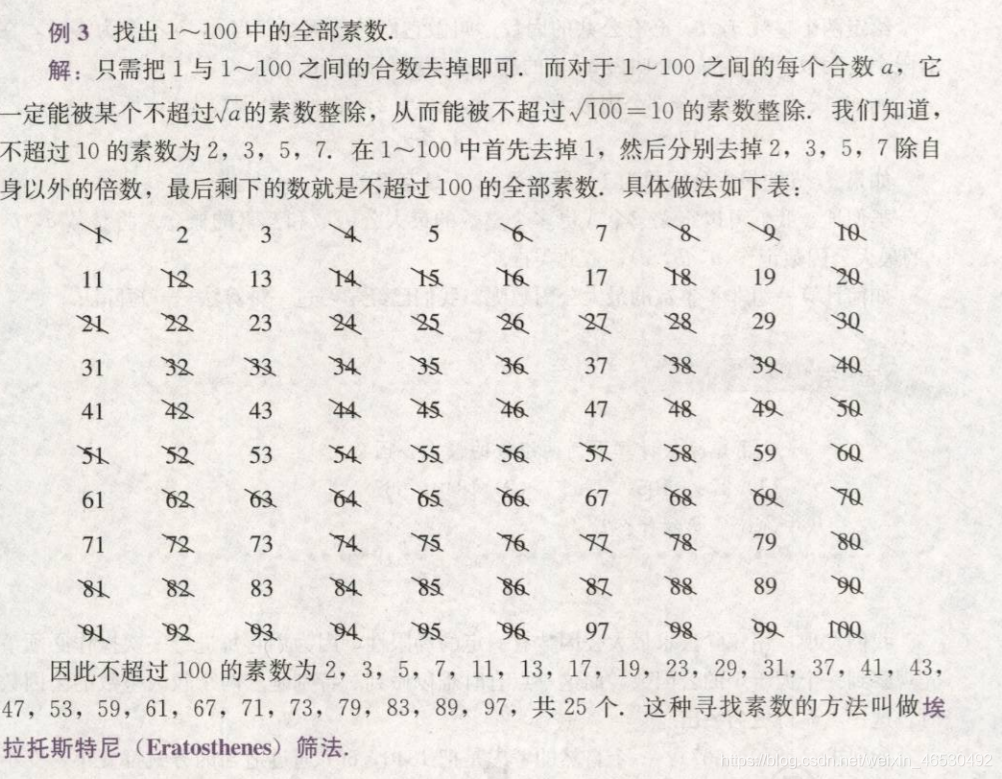
n=int(input())
v=[0 for i in range(n+1)] #初始化全为0
v[1]=1 
for i in range(2,n+1):
    if v[i]==0:        
        for j in range(2*i,n+1,i):            
            v[j]=1    #所有i的倍数标记为1
for i in range(2,n+1):
    if v[i]==0:
        print(i)

算法的时间复杂度为 $O(nlog(logn))$。
但是我们仍然可以发现，j是从2 * i开始计数的，实际上2 * i是2的倍数，在筛2的倍数的时候已经筛掉了，3 * i是3的倍数，在筛3的倍数的时候也已经筛掉了，所有小于i * i 的倍数其实都被筛掉了，因此j的起始值可以取 i * i。上述方法简称埃氏筛法。
把开平方法和上述程序结合起来的结果似乎和把2 * i改成i * i的结果等同。
（4）欧式筛法
对于一般的数据，埃氏筛法已经足够了，但是进一步优化，我们仍然能找到埃氏筛法的一些不足。
比如2已经把6筛掉了，3又筛了一次。也就是说素数的公倍数会被这些素数重复筛，这显然是不必要的。所以欧式筛法和埃氏筛法的区别就在于欧式筛法每个数只筛一次。
（5）Miller-Rabin算法和Pollard-Rho算法
除此之外，还有一些素数测试算法，在牺牲一小部分正确率来降低时间复杂度的方法，可以移步这篇文章