带你手写红黑树（上）原理篇

当你在查找红黑树的教程时，相信你早已熟悉二叉查找树。

因此，本文不再对二叉查找树的基础操作进行讲解。

本文必要的代码使用 C++ 给出。

话不多说，进入正文。

一、红黑树的规则

节点是红色或者黑色
根节点是黑色
每个叶子节点都是黑色的空节点
每个红节点的两个子节点都必须是黑色
从任意节点到其叶子节点的所有路径都包含相同数目的黑色节点

默认规则：新插入节点是红色

二、红黑树的节点定义

enum Color :bool { RED = 0, BLACK };
struct Node
{
	_Ty key;
	Node* left = nullptr;
	Node* right = nullptr;
	Node* parent = nullptr;
	Color color = RED;	// 新插入节点为红色
	Node(const _Ty& _key) :key(_key) {}
};

enum Color :bool { RED = 0, BLACK };：定义节点颜色
_Ty：键值 key 的类型
left：左节点指针
right：右节点指针
parent：父节点指针
color：节点颜色

三、什么是旋转操作

红黑树自平衡过程中需要使用两个操作：旋转、变色。

变色很容易理解，旋转是怎么回事呢？

旋转包括左旋和右旋。

讲解旋转前，给出本文绘图讲解中的一些规范：

圆形代表一个节点
梯形代表一棵子树：可空，可只有一个节点的节点，可有多于一个节点的子树

下面讲解左旋和右旋。

左旋

下图便是左旋操作，本文规定：称 X 左旋

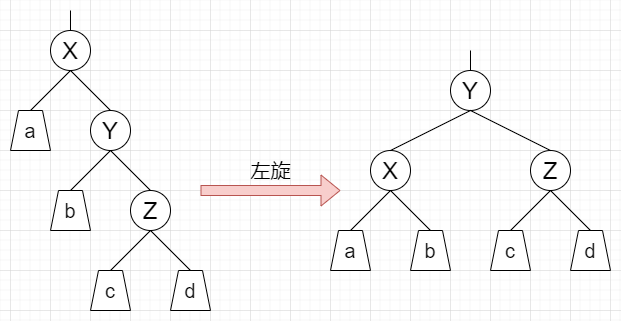
右旋

下图便是右旋操作，本文规定：称 X 右旋

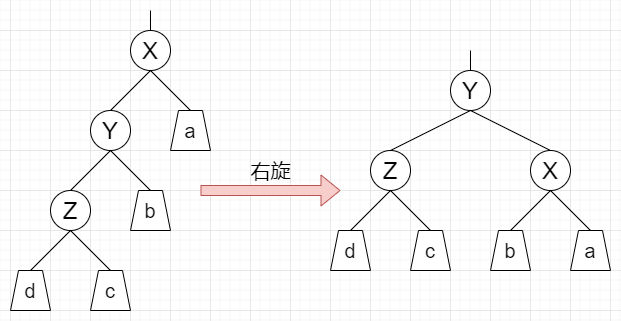
注意

写代码时注意各个节点指针指向的改变，X 父节点同样参与
另外，具体操作比较啰嗦，这里就不进行文字说明，你可以对比我的代码去体会

四、红黑树的插入操作

本文规定：插入的节点为 cur，cur 的父亲节点为 par，cur 的叔叔节点为 uncle，cur 的爷爷节点为 gpa

case 1：

树空，则插入节点将作为根节点，变色为黑色（新插入节点默认红色），结束

case 2：

par 是黑色，结束（因为这不会违背红黑树规则）

case 3：

par 是红色：违背规则 4，需要调整使得红黑树重新符合规则。

uncle 是红色：par、uncle 变黑，gpa 变红（若此时 gpa 是根节点，将 gpa 变黑即可，结束），cur 重新指向 gpa，回溯
uncle 是黑色：旋转变色，结束；经过旋转变色后，红黑树重新符合规则；旋转变色根据下列情况进行：
- par 是 gpa 左孩子
  - cur 是 par 左孩子：右旋 gpa（类似 AVL 树中的左左_右旋），交换 par 和 gpa 的颜色
  - cur 是 par 右孩子：先左旋 par，再右旋 gpa（类似 AVL 树中的左右_左右旋），交换 cur 和 gpa 的颜色
- par 是 gpa 右孩子（与上面左右对称，就不再贴图）
  - cur 是 par 左孩子：先右旋 par，再左旋 gpa（类似 AVL 树中的右左_右左旋），交换 cur 和 gpa 的颜色
  - cur 是 par 右孩子：左旋 gpa（类似 AVL 树中的右右_左旋），交换 par 和 gpa 的颜色

五、红黑树的删除操作

红黑树难，难就难在删除上，而插入操作你也看到了，其实并不难。

这里简单分析一下（也是一个小小的总结）：

插入操作：
- 插入位置固定，是插入到叶子节点处
- 除开插入为根节点的情况，其实只有两种情况，父节点为红色或黑色，而稍微复杂一点的是父节点为红色，这个时候若叔叔节点为红色，则变色回溯，反之经过旋转变色即可。
删除操作：
- 删除的节点可能是红色，可能是黑色
- 删除的节点可能有两个孩子，可能有一个孩子，还可能没有孩子
- 如此，似乎就有 2*3=6 种情况了，还需要考虑删除根节点的情况
- 仅删除的节点便有这么多可能，如果调整时每一种还对应多种情况，其复杂程度可想而知

当然，实际上没有这么多情况，也没有这么复杂，正是在红黑树五条规则的约束下，红黑树会变得简单。

提前透露一下，删除操作真正复杂的只有一种情况：删除节点是黑色且无孩子。

在进入删除操作讲解之前，先看一下在红黑树规则约束下一下隐藏的特性，正因此红黑树变得没这么难。

红黑树隐藏特性

红节点要么没有孩子，要么有两个孩子，不存在只有一个孩子的情况
黑节点只有一个孩子时，该孩子一定是红色，且该孩子无孩子

上面两点，应该不难理解，证明：

若红节点（令其为 pr）只有一个孩子：若为红，则违背规则 4；若为黑，则 pr 违背规则 5。
黑节点（令其为 pb）只有一个孩子时，若为黑，则 pb 违背规则 5。

接下来正式开始讲解红黑树删除操作。

绘图讲解中，本文规定：红节点用红色填充，黑节点用黑色填充，未知颜色不填充。

本文规定：待删除节点为 cur，cur 的父亲为 par，cur 的兄弟为 bro，bro 的左孩子为 LC，右孩子为 RC。

case 1：cur 是红色

cur 没有孩子：直接删除 cur 即可，结束（这不会违背任何规则）
cur 有两个孩子：寻找左子树最大的节点或右子树最小的节点（令其为 del），用 del 的键值取代 cur 的键值（但不取代 cur 的颜色），然后递归调用删除 del
cur 只有一个孩子：该情况不存在，见上文隐藏规则

case 2：cur 是黑色

cur 有两个孩子：同上处理，寻找左子树最大的节点或右子树最小的节点（令其为 del），用 del 的键值取代 cur 的键值（但不取代 cur 的颜色），然后递归调用删除 del
cur 只有一个孩子：由隐藏规则知道，该孩子一定是红色，则将 cur 的键值用该红孩子的键值代替（但不取代 cur 的颜色），然后直接删除 del 即可，结束
cur 没有孩子（这是最复杂的情况）
- 分析：cur 没有孩子，且 cur 是黑色，删除之后，par 在 cur 支路会少一个黑节点，所以要想办法补充这个缺失的黑节点
- 这是最后也是最复杂的情况，后面重点讲解

删除节点 cur 是黑色且无孩子

bro 是红色
- cur 是 par 的左孩子：左旋 par，交换 par 和 bro 的颜色，将 bro 重新指向 par 的右孩子，此时 par 左边任然少一个黑色节点，但是此时符合后面的情况：bro 是黑色，par 是红色，因此交给后面的情况处理
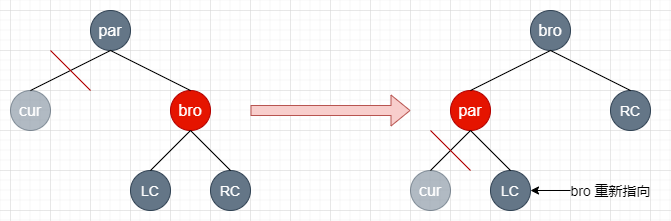
- cur 是 par 的右孩子，与上面左右对称，读者自行思考
bro 是黑色

同样看 cur 是 par 的左孩子还是右孩子，下面以 cur 是 par 左孩子为例绘图讲解，cur 是 par 右孩子与 cur 是 par 左孩子的情况左右对称，交给读者自行思考
- RC 是红色：左旋 par，交换 par 和 bro 的颜色，RC 变黑色，结束
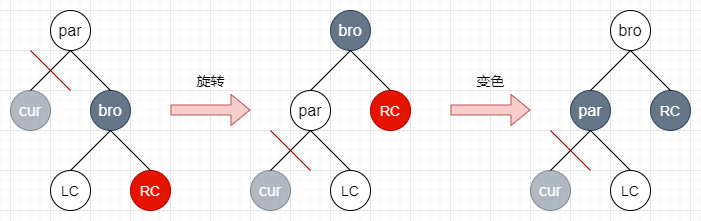
- LC 是红色：右旋 bro，左旋 par，LC 的颜色置为 par 的颜色，par 变黑色，结束
- par 是红色：交换 par 和 bro 的颜色，结束
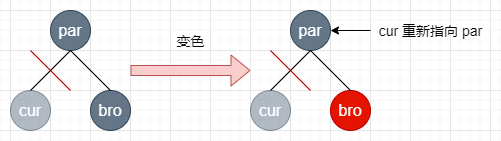
- par 是黑色，bro 是黑色（排除了上面的情况，这是最后一种情况，此时 bro 无孩子）：bro 变红，但是 par 的父亲节点在 par 支路少一个黑色节点，此时：
  - 若 par 是根节点，结束
  - 否则 cur 指向 par，回溯