高效进行模幂运算

高效进行模幂运算

一、题目描述

你的任务是计算 a^b 对 1337 取模，a 是一个正整数，b 是一个非常大的正整数且会以数组形式给出。

示例 1:

输入: a = 2, b = [3]
输出: 8

示例 2:

输入: a = 2, b = [1,0]
输出: 1024

二、分析

单就这道题可以有三个难点：

• 一是如何处理用数组表示的指数，现在 b 是一个数组，也就是说 b可以非常大，没办法直接转成整型，否则可能溢出。你怎么把这个数组作为指数，进行运算呢？
• 二是如何得到求模之后的结果？按道理，起码应该先把幂运算结果算出来，然后做 % 1337 这个运算。但问题是，指数运算你懂得，真实结果肯定会大得吓人，也就是说，算出来真实结果也没办法表示，早都溢出报错了。
• 三是如何高效进行幂运算，进行幂运算也是有算法技巧的，如果你不了解这个算法，后文会讲解。

那么对于这几个问题，我们分开思考，逐个击破。

如何处理数组指数：

• 首先明确问题：现在 b 是一个数组，不能表示成整型，而且数组的特点是随机访问，删除最后一个元素比较高效。
• 不考虑求模的要求，以 b = [1,5,6,4] 来举例，结合指数运算的法则，我们可以发现这样的一个规律：

看到这，我们的老读者肯定已经敏感地意识到了，这就是递归的标志呀！因为问题的规模缩小了：

    superPow(a, [1,5,6,4])
=>  superPow(a, [1,5,6])

那么，发现了这个规律，我们可以先简单翻译出代码框架：

// 计算 a 的 k 次方的结果
// 后文我们会手动实现
int mypow(int a, int k);

int superPow(int a, vector<int>& b) 
{
    // 递归的 base case
    if (b.empty()) 
    	return 1;
    
    // 取出最后一个数
    int last = b.back();
    b.pop_back();
    
    // 将原问题化简，缩小规模递归求解
    int part1 = mypow(a, last);
    int part2 = mypow(superPow(a, b), 10);
    
    // 合并出结果
    return part1 * part2;
}

到这里，应该都不难理解吧！我们已经解决了 b 是一个数组的问题，现在来看看如何处理 mod，避免结果太大而导致的整型溢出。

如何处理 mod 运算：

• 首先明确问题：由于计算机的编码方式，形如 (a * b) % base这样的运算，乘法的结果可能导致溢出，我们希望找到一种技巧，能够化简这种表达式，避免溢出同时得到结果。
• 比如在二分查找中，我们求中点索引时用 (l+r)/2 转化成 l+(r-l)/2，避免溢出的同时得到正确的结果。
• 那么，说一个关于模运算的技巧吧，毕竟模运算在算法中比较常见：
  (a * b) % k = (a % k)(b % k) % k

证明很简单，假设：
a = Ak +B；b = Ck + D

其中 A,B,C,D 是任意常数，那么：
ab = ACk^2 + ADk + BCk +BD

ab % k = BD % k

又因为：
a % k = B；b % k = D

所以：
(a % k)(b % k) % k = BD % k
综上，就可以得到我们化简求模的等式了。

• 换句话说，对乘法的结果求模，等价于先对每个因子都求模，然后对因子相乘的结果再求模。
• 那么扩展到这道题，求一个数的幂不就是对这个数连乘么？所以说只要简单扩展刚才的思路，即可给幂运算求模：

三、代码

int base = 1337;

// 计算 a 的 k 次方然后与 base 求模的结果
int mypow(int a, int k) 
{
    // 对因子求模
    a %= base;
    int res = 1;
    for (int _ = 0; _ < k; _++) 
    {
        // 这里有乘法，是潜在的溢出点
        res *= a;
        
        // 对乘法结果求模
        res %= base;
    }
    return res;
}

int superPow(int a, vector<int>& b) 
{
    if (b.empty()) 
    	return 1;
    
    int last = b.back();
    b.pop_back();

    int part1 = mypow(a, last);
    int part2 = mypow(superPow(a, b), 10);
    
    // 每次乘法都要求模
    return (part1 * part2) % base;
}

• 你看，先对因子 a 求模，然后每次都对乘法结果 res 求模，这样可以保证 res *= a 这句代码执行时两个因子都是小于base 的，也就一定不会造成溢出，同时结果也是正确的。
• 至此，这个问题就已经完全解决了，已经可以通过 LeetCode 的判题系统了。
  但是有的读者可能会问，这个求幂的算法就这么简单吗，直接一个 for 循环累乘就行了？复杂度会不会比较高，有没有更高效地算法呢？
• 有更高效地算法的，但是单就这道题来说，已经足够了。
• 因为你想想，调用 mypow 函数传入的 k 最多有多大？k 不过是 b 数组中的一个数，也就是在 0 到 9 之间，所以可以说这里每次调用 mypow 的时间复杂度就是 O(1)。整个算法的时间复杂度是 O(N)，N 为 b 的长度。

如何高效求幂：
快速求幂的算法不止一个，就说一个我们应该掌握的基本思路吧。利用幂运算的性质，我们可以写出这样一个递归式：

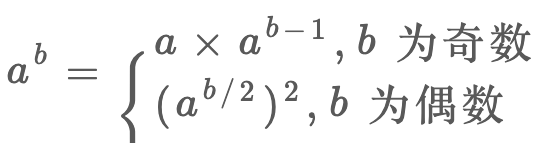
• 这个思想肯定比直接用 for 循环求幂要高效，因为有机会直接把问题规模（b 的大小）直接减小一半，该算法的复杂度肯定是 log级了。
• 那么就可以修改之前的 mypow 函数，翻译这个递归公式，再加上求模的运算：

int base = 1337;

int mypow(int a, int k) 
{
    if (k == 0) 
    	return 1;
    
    a %= base;

    if (k % 2 == 1) 
    {
        // k 是奇数
        return (a * mypow(a, k - 1)) % base;
    } 
    else 
    {
        // k 是偶数
        int sub = mypow(a, k / 2);
        return (sub * sub) % base;
    }
}