引言
这是统计学习方法的读书笔记。主要讲了提升方法,这是一种常用的机器学习方法。在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,可以提高分类的性能。
上周看了这一章,再不记录下来自己都要忘记了
首先介绍代表性的提升方法AdaBoost。
AdaBoost方法
提升方法的基本思路
提升方法基于这样一种思想:对于一个复杂任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好。
在概率近似正确学习的框架中,一个概念(一个类),如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的;如果学习的正确率只比随机猜测略好,那么就称这个概念是弱可学习的。后来证明强可学习与弱可学习是等价的。
这样一来,在机器学习中,如果已经发现了弱可学习算法,那么能否将它提升(boost)为强可学习算法。因为发现弱可学习算法要容易的多。
大多数的提升方法都是改变训练数据的概率分布(训练数据的权值分布),针对不同的训练数据分布调用弱可学习算法学习一系列弱分类器,最终将这些弱分类器组合成一个强分类器。
AdaBoost算法
假设给定一个二分类的训练数据集
T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中,每个样本点由实例与标记组成。实例
xi∈X⊆Rn,标记
yi∈Y={−1,+1}。
这里要注意的是
Y的取值不是
{1,0},而是
{−1,+1}。
AdaBoost
输入:训练数据集
T;弱可学习算法;
输出:最终分类器
G(x)
-
初始化训练数据的权值分布(初始为同样的均值)
D1=(w11,⋯,w1i,⋯,w1N),w1i=N1,i=1,2,⋯,N
-
对于
m=1,2,⋯,M(对应于
M个模型)
a. 使用具有权值分布
Dm的训练数据集学习,得到基本分类器
Gm(x):X→{−1,+1}
b.计算
Gm(x) 在训练数据集上的分类误差率
em=i=1∑NP(Gm(xi)=yi)=i=1∑NwmiI(Gm(x)=yi)(8.1)
这里的
I是指示函数,里面的条件成立返回
1,否则返回
0。
分类误差率 = 判断结果不等于真实结果的概率,考虑权重的话,也就是计算分类错误的样本权重之和。一般我希望误差率要比随机猜测要好,可以去掉比随机猜测差的模型,或进行一些处理(下面的实例可以看到是如何处理的),以保证
em≤0.5。
c. 计算
Gm(x)的系数(该模型的权重)
αm=21logem1−em(8.2)
因为我们说
em≤0.5,所以权重必然是大于等于0的。这一点很重要,我们可以通过它的函数图像来验证

并且
αm随着
em的减小而增大,所以分类误差率越小的基本分类器在最终分类器中的作用越大。
d. 更新训练数据的权值分布(增大误分类点的权重)
Dm+1=(wm+1,1,⋯,wm+1,i,⋯,wm+1,N)(8.3)
wm+1,i=Zmwmiexp(−αmyiGm(xi)),i=1,2,⋯,N(8.4)
这里
Zm是规范化因子
Zm=i=1∑Nwmiexp(−αmyiGm(xi))(8.5)
它使
Dm+1成为一个概率分布。
这段比较长,先看下这个式子
yiGm(xi),当预测正确的时候,这个式子的结果是
+1,同号相乘得正数;预测错误的时候为
−1。所当预测正确的时候,
exp(−αmyiGm(xi))的结果就是
exp(−αm);当预测错误的时候结果就是
exp(αm)。
exp(−αmyiGm(xi))={exp(−αm)exp(αm):yi=Gm(xi):yi=Gm(xi)
上面我们说过
em≤0.5,当然
em≥0的。这里作为一个概率不能为负的。

而
ex的图像是这样的:

当分类正确时
exp(−αm)<1,根据
wm+1,i=Zmwmiexp(−αmyiGm(xi)),也就是分类正确的样本权值会比之前的要小,反之,分类错误的样本权值要比之前要大。
那这里除以一个
Zm是干嘛的呢?看这个
Zm的式子,其实就是所有样本权值之和,让
wmiexp(−αmyiGm(xi))除以
Zm就可以让
i=1∑Nwm+1,i=1
使得
Dm+1成为一个概率分布。
- 在构建好
M个基本分类器模型后,最终构建基本分类器的线性组合
f(x)=m=1∑MαmGm(x)(8.6)
得到最终分类器
G(x)=sign(f(x))=sign(m=1∑MαmGm(x))(8.7)
其中
sign是符号函数。
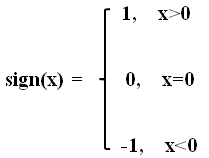
每个分类器误差率越小,权重越大。
如果上面的公式没看懂的话没关系,我们来看一个例子。
AdaBoost的例子(代码实现)
给定如表8.1所示训练数据,假设弱分类器由
x<v或
x>v产生,其阈值
v使该分类器在训练数据集上分类误差率最低。用AdaBoost算法学习一个强分类器。

这里根据书上的过程自己算一遍也很简单,不过要注意的是,当误差率大于
0.5时,这里直接取反即可。比如在
x<v的情况下,就是把
x<v 改成
x>v。
这里把整个过程用代码实现了一遍
import numpy as np
import math
import collections
Classifier = collections.namedtuple('Classifier', ['alpha', 'split', 'sign'])
class AdaBoost:
def __init__(self, M):
self.M = M
self.f = []
def Gm(self, split, sign=1):
r = self.x.copy()
r[r < split] = 1 * sign
r[r > split] = -1 * sign
return r
def cal_alpha(self, error):
return round(1 / 2 * math.log((1 - error) / error, math.e), 4)
def update_weight(self, split, alpha, sign=1):
g = self.Gm(split, sign)
exp_result = np.exp(-1 * alpha * self.y * g)
Z = np.sum(self.w * exp_result)
return np.round(self.w * exp_result / Z, 5)
def cal_error_count(self):
result = np.zeros((self.size,))
for alpha, split, sign in self.f:
result += alpha * self.Gm(split, sign)
return sum(np.sign(result) != self.y)
def choose_best_split(self):
best_v, min_error, best_sign = -1, 1, 1
for i in range(1, self.size):
v = (self.x[i - 1] + self.x[i]) / 2
sign = 1
error = sum(self.w[self.Gm(v) != self.y])
if error > 0.5:
error = 1 - error
sign = -1
if error < min_error:
best_v = v
min_error = error
best_sign = sign
print('best v:%s,best error :%s,error elements:%s' % (
best_v, min_error, self.x[self.Gm(best_v, best_sign) != self.y]))
return best_v, min_error, best_sign
def fit(self, x, y):
x.sort()
self.x = x
self.y = y
self.size = len(x)
self.w = np.ones((self.size,)) / self.size
for m in range(self.M):
split, error, sign = self.choose_best_split()
alpha = self.cal_alpha(error)
self.w = self.update_weight(split, alpha, sign)
self.f.append(Classifier(alpha, split, sign))
error_count = self.cal_error_count()
if error_count == 0:
break
def _predict(self, single_x):
result = 0
for alpha, split, sign in self.f:
result += alpha * (sign if single_x < split else -1 * alpha)
return np.sign(result)
def predict(self, x_test):
return np.array([self._predict(r) for r in x_test])
def __repr__(self):
lc = ''
for c in self.f:
lc = lc + '%.4fGm(x,%s,%d)' % (c.alpha, c.split, c.sign) + '+'
lc = lc[:-1]
return 'sign[%s](error count is %d)' % (lc, self.cal_error_count())
if __name__ == '__main__':
x = np.arange(10)
y = np.array([1,1,1,-1,-1,-1,1,1,1,-1])
ab = AdaBoost(5)
ab.fit(x,y)
print(ab)
print(ab.predict(np.array([3,1,5])))
这里只学习了3个模型就可以达到准确率为100%了。
best v:2.5,best error :0.30000000000000004,error elements:[6 7 8]
best v:8.5,best error :0.21428999999999998,error elements:[3 4 5]
best v:5.5,best error :0.1818399999999999,error elements:[0 1 2 9]
并且输出了最终分类器:
sign[0.4236Gm(x,2.5,1)+0.6496Gm(x,8.5,1)+0.7520Gm(x,5.5,-1)](error count is 0)
可以根据这个代码结合书上的讲解去理解AdaBoost的思想。
AdaBoost算法的训练误差分析
AdaBoost能在学习过程中不断减少训练误差,即在训练数据集上的分类误差率。
这个误差率可以用下面的公式来计算:
N1i=1∑NI(G(xi)=yi)
这里的
G(x) 为
G(x)=sign(m=1∑MαmGm(x))
定理8.1 AdaBoost的训练误差界
N1i=1∑NI(G(xi)=yi)≤N1i∑exp(−yif(xi))=m∏Zm(8.9)
我们先看
N1∑i=1NI(G(xi)=yi)≤N1∑iexp(−yif(xi))
这里的
I是指示函数,里面的条件成立返回
1,否则返回
0。
首先对于正确分类的点来说(指示函数里面的条件不成立),
I(G(xi)=yi)=0≤exp(−yif(xi))=e−1
对于错误分类的点来说(指示函数里面的条件成立),
I(G(xi)=yi)1≤exp(−yif(xi))=e1
所以式
(8.9)第一个不等号是很好推的,接下来推右边的等式。
Zm在
(8.4)和
(8.5)中出现。

先对
(8.4)进行一个变形,把分母上的
Zm乘到左边去:
Zm⋅wm+1,i=wmiexp(−αmyiGm(xi))
这里说的是样本下一轮的权重和本轮的权重之间的关系。
因为这里有个
wm+1,1,我们可以想到
Z1⋅w2,i=w1,iexp(−α1yiG1(xi))Z2⋅w3,i=w2,iexp(−α2yiG2(xi))⋮ZM−1⋅wM,i=wM−1,iexp(−αM−1yiGM−1(xi))
如果把上面这很多个式子中,等式左边相乘,等式右边也相乘的话,可以约掉相同项,得:
Z1⋅w2,i
=w1,iexp(−α1yiG1(xi))Z2⋅w3,i
=w2,i
exp(−α2yiG2(xi))⋮ZM−1⋅wM,i=wM−1,i
exp(−αM−1yiGM−1(xi))
整理一下得(右边利用了
ea⋅eb=ea+b)
m∏M−1Zm⋅WM,i=w1,iexp(−yim=1∑M−1αmGm(xi))
观察上式和
(8.9)式的区别可知上式中,左边少了个
ZM,多了个
WM,i;右边指数函数中少加了个
αMGM(xi))
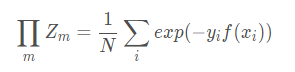
我们让左右两边同时乘以
exp(−yiαMGM(xi)),
m∏M−1Zm⋅WM,i⋅exp(−yiαMGM(xi))=N1exp(−yim=1∑M−1αmGm(xi))⋅exp(−yiαMGM(xi))
因为
w1,i是首轮的权值,为
N1,把上式左边整理一下得:
m∏M−1Zm⋅WM,i⋅exp(−yiαMGM(xi))=N1exp(−yim=1∑MαmGm(xi))
上面得到的式子是针对单个样本点
i的,而
(8.9)是针对所有样本点的,所以两边都对所有样本点求和得:
m∏M−1Zm⋅i=1∑NWM,i⋅exp(−yiαMGM(xi))=N1i=1∑N(exp(−yim=1∑MαmGm(xi)))
根据公式
(8.5)和公式
(8.6),得
m∏MZm=N1i=1∑Nexp(−yif(xi))
证明完毕。
这个定理告诉我们,训练误差可以表示为
Zm的连乘。我们要让训练误差比较小的话,只要最小化每个
Zm就可以了。
Zm=i=1∑Nwmiexp(−αmyiGm(xi))
再来看下
Zm的式子,我们再每个循环里面,
wmi是上一轮循环里面得到的,
Gm是本轮训练得到的。未知的是
αm,我们就可以通过最小化
Zm来求
αm。
令
∂αm∂Zm=0,这样可以求得最小的
αm为下式:
αm=21logem1−em
这也是书上为我们提供的计算方法。
定义8.2 二分类问题AdaBoost的训练误差界
m=1∏MZm=m=1∏M[2em(1−em)
]=m=1∏M1−4γm2
≤exp(−2m=1∑Mγm2)(8.10)
这里
γ=21−em

证明,由式
(8.5)和
(8.8)得
Zm=i=1∑Nwmiexp(−αmyiGm(xi))=yi=Gm(xi)∑wmie−αm+yi=Gm(xi)∑wmieαm
这一步就是根据
yiGm(xi)在判断正确的情况下为
+1,错误的情况下为
−1得到的。
Zm=i=1∑Nwmiexp(−αmyiGm(xi))=yi=Gm(xi)∑wmie−αm+yi=Gm(xi)∑wmieαm=(1−em)e−αm+emeαm
这一步是当
yi=Gm(xi)时,对判断结果求乘以一个
−1。
Zm=i=1∑Nwmiexp(−αmyiGm(xi))=yi=Gm(xi)∑wmie−αm+yi=Gm(xi)∑wmieαm=(1−em)e−αm+emeαm=2em(1−em)
=1−4γm2
那么不等式
m=1∏M1−4γm2
≤exp(−2m=1∑Mγm2)
是怎么证明的呢,书上给出了提示,用泰勒展开式。
我们先去掉连乘符号。
右边有
exp(−2m=1∑Mγm2)=m=1∏Mexp(−2γm2)
也就是只要证明
1−4γ2
≤exp(−2γ2)
关于泰勒公式,可以参阅人工智能数学基础之高等数学
下面用泰勒展开来证明,利用点
x=0 的泰勒展开式,
首先看
1−4γ2
的泰勒展开,可以令
4γ2=x,也就是
f(x)=1−x
=(1−x)21。我们要求泰勒展开,就是要求
f(x)的导数,这里只要求前两阶导数就够了。
f(x)=(1−x)21f′(x)=−21(1−x)−21f′′(x)=−41(1−x)−23
那么
f(x)=f(0)+xf′(0)+21x2f′′(0)+⋯≈1−21x−81x2
把
4γ2代入上式中
x得
f(4γ2)≈1−2γ2−2γ4
接下来来看
exp(−2γ2),令
−2γ2=x,得
g(x)=ex
g(x)=exg′(x)=exg′′(x)=ex
那么
g(x)=g(0)+xg′(0)+21x2g′′(0)+⋯≈1+21x+21x2
g(−2γ2)≈1−2γ2+2γ4
这里
γ=21−em,因此
γ的取值范围是
[0,21],因为
em≤21
所以当更高阶出现的时候,后面的高阶项约等于0了。
所以只要判断
f(4γ2)≈1−2γ2−2γ4
和
g(−2γ2)≈1−2γ2+2γ4的大小即可。
显然
1−2γ2−2γ4≤1−2γ2+2γ4,当
em=21时,
γ=0,不等式两边相等。
证明完毕。
m=1∏MZm≤exp(−2m=1∑Mγm2)
这个式子有什么意义了呢,因为
γ的取值范围是
[0,21],说明训练误差会随着训练论轮数的增加而减少;同时训练误差是以指数速率下降的。
AdaBoost算法的解释
AdabBoost算法还有另一个解释,即可以认为AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分布算法时的二分类学习方法。
前向分步算法
考虑加法模型(additive model)
f(x)=m=1∑Mβmb(x;γm)(8.13)
其中,
b(x;γm)为基函数,
γm为基函数的参数。显然式
(8.6)是一个加法模型。
前向分布算分的步骤如下:
- 初始化
f0(x)=0
- 对
m=1,2,⋯,M
- 极小化损失函数
(βm,γm)=argβ,γmini=1∑NL(yi,fm−1(xi)+βb(xi;γ))(8.16)
得到参数
βm,γm
- 更新
fm(x)=fm−1(x)+βmb(x;γm)(8.17)
- 得到加法模型
f(x)=fM(x)=m−1∑Mβmb(x;γm)(8.18)
这样前向分步算分将同时求解从
m=1到
M所有参数
βm,γm的优化问题简化为逐次求解各个
βm,γm的优化问题。
AdaBoost算分是前向分布加法算分的特例,这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。
提升树
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree) 。
对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。
提升树模型可以表示为决策树的加法模型:
fM(x)=m=1∑MT(x;Θm)
关于代码示例可见机器学习入门——图解集成学习(附代码)
参考
- 统计学习方法



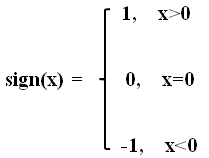


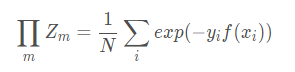


 博客专家
博客专家