二进制编码
理解二进制的“逢二进一”
二进制和我们平时用的十进制,其实并没有什么本质区别,只是平时我们是“逢十进一”,这里变成了“逢二进一”而已。每一位,相比于十进制下的 0~9 这十个数字,我们只能用 0 和 1 这两个数字。
任何一个十进制的整数,都能通过二进制表示出来。把一个二进制数,对应到十进制,非常简单,就是把从右到左的第 N 位,乘上一个 2 的 N 次方,然后加起来,就变成了一个十进制数。当然,既然二进制是一个面向程序员的“语言”,这个从右到左的位置,自然是从 0 开始的。
比如 0011 这个二进制数,对应的十进制表示,就是
,代表十进制的 3。
对应地,如果我们想要把一个十进制的数,转化成二进制,使用短除法就可以了。也就是,把十进制数除以 2 的余数,作为最右边的一位。然后用商继续除以 2,把对应的余数紧靠着刚才余数的右侧,这样递归迭代,直到商为 0 就可以了。
比如,我们想把 13 这个十进制数,用短除法转化成二进制,需要经历以下几个步骤:
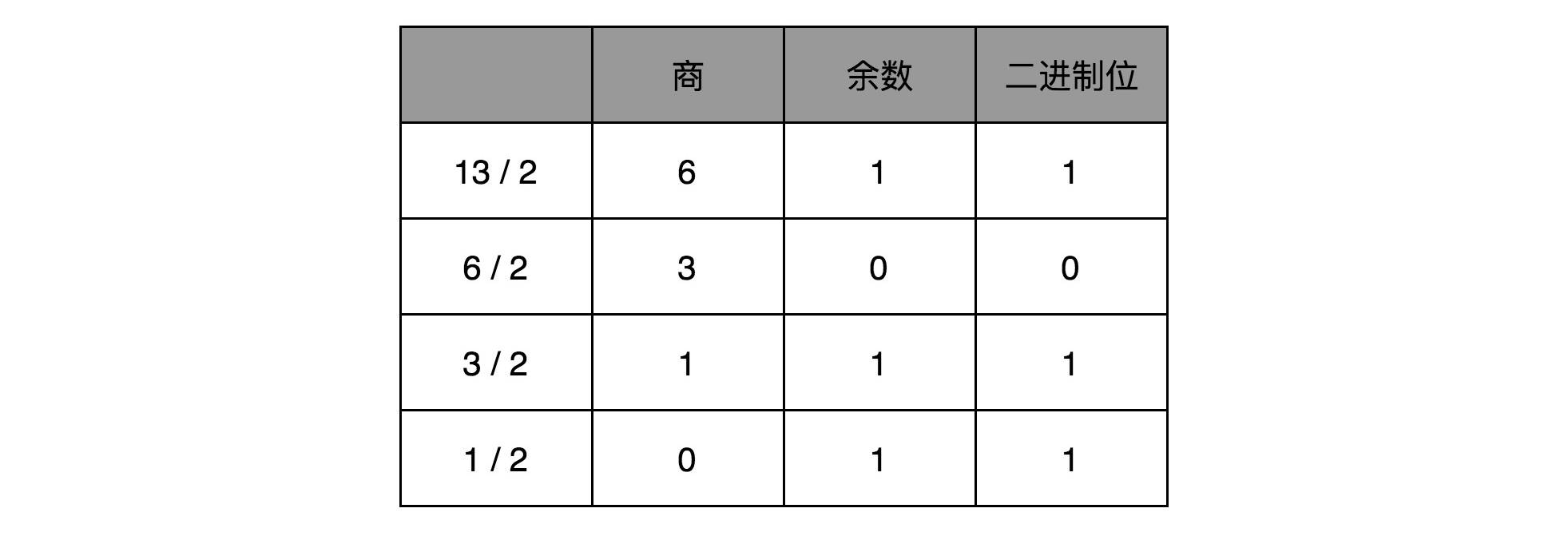
因此,对应的二进制数,就是 1101。
刚才我们举的例子都是正数,对于负数来说,情况也是一样的吗?我们可以把一个数最左侧的一位,当成是对应的正负号,比如 0 为正数,1 为负数,这样来进行标记。
这样,一个 4 位的二进制数, 0011 就表示为 +3。而 1011 最左侧的第一位是 1,所以它就表示 -3。这个其实就是整数的原码表示法。原码表示法有一个很直观的缺点就是,0 可以用两个不同的编码来表示,1000 代表 0, 0000 也代表 0。习惯万事一一对应的程序员看到这种情况,必然会被“逼死”。
于是,我们就有了另一种表示方法。我们仍然通过最左侧第一位的 0 和 1,来判断这个数的正负。但是,我们不再把这一位当成单独的符号位,在剩下几位计算出的十进制前加上正负号,而是在计算整个二进制值的时候,在左侧最高位前面加个负号。
比如,一个 4 位的二进制补码数值 1011,转换成十进制,就是
如果最高位是 1,这个数必然是负数;最高位是 0,必然是正数。并且,只有 0000 表示 0,1000 在这样的情况下表示 -8。一个 4 位的二进制数,可以表示从 -8 到 7 这 16 个整数,不会白白浪费一位。
当然更重要的一点是,用补码来表示负数,使得我们的整数相加变得很容易,不需要做任何特殊处理,只是把它当成普通的二进制相加,就能得到正确的结果。
我们简单一点,拿一个 4 位的整数来算一下,比如 -5 + 1 = -4,-5 + 6 = 1。我们各自把它们转换成二进制来看一看。如果它们和无符号的二进制整数的加法用的是同样的计算方式,这也就意味着它们是同样的电路。
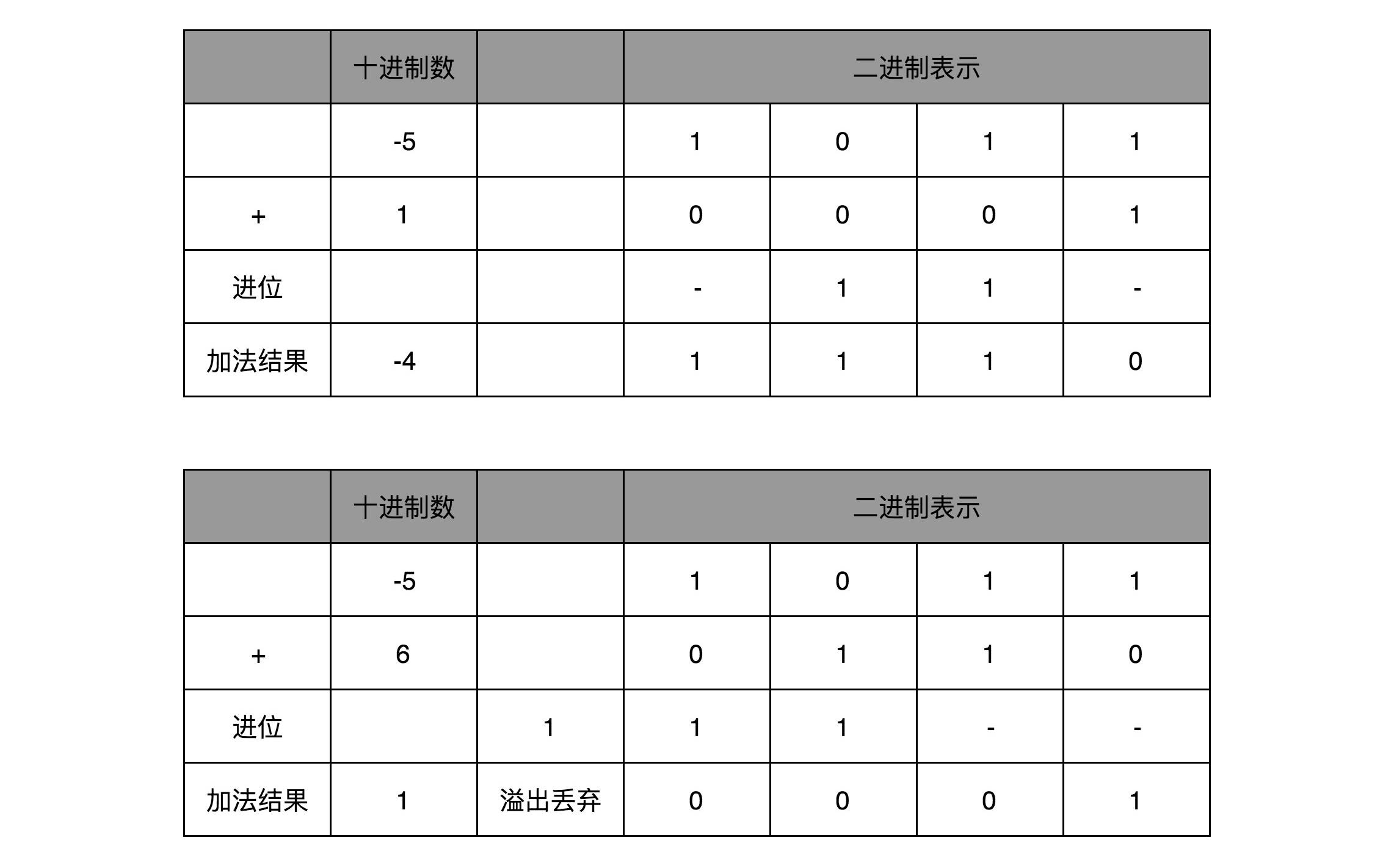
字符串的表示,从编码到数字
不仅数值可以用二进制表示,字符乃至更多的信息都能用二进制表示。最典型的例子就是字符串(Character String)。最早计算机只需要使用英文字符,加上数字和一些特殊符号,然后用 8 位的二进制,就能表示我们日常需要的所有字符了,这个就是我们常常说的ASCII 码(American Standard Code for Information Interchange,美国信息交换标准代码)。

ASCII 码就好比一个字典,用 8 位二进制中的 128 个不同的数,映射到 128 个不同的字符里。比如,小写字母 a 在 ASCII 里面,就是第 97 个,也就是二进制的 0110 0001,对应的十六进制表示就是 61。而大写字母 A,就是第 65 个,也就是二进制的 0100 0001,对应的十六进制表示就是 41。
在 ASCII 码里面,数字 9 不再像整数表示法里一样,用 0000 1001 来表示,而是用 0011 1001 来表示。字符串 15 也不是用 0000 1111 这 8 位来表示,而是变成两个字符 1 和 5 连续放在一起,也就是 0011 0001 和 0011 0101,需要用两个 8 位来表示。
我们可以看到,最大的 32 位整数,就是 2147483647。如果用整数表示法,只需要 32 位就能表示了。但是如果用字符串来表示,一共有 10 个字符,每个字符用 8 位的话,需要整整 80 位。比起整数表示法,要多占很多空间。
这也是为什么,很多时候我们在存储数据的时候,要采用二进制序列化这样的方式,而不是简单地把数据通过 CSV 或者 JSON,这样的文本格式存储来进行序列化。不管是整数也好,浮点数也好,采用二进制序列化会比存储文本省下不少空间。
ASCII 码只表示了 128 个字符,一开始倒也堪用,毕竟计算机是在美国发明的。然而随着越来越多的不同国家的人都用上了计算机,想要表示譬如中文这样的文字,128 个字符显然是不太够用的。于是,计算机工程师们开始各显神通,给自己国家的语言创建了对应的字符集(Charset)和字符编码(Character Encoding)。
字符集,表示的可以是字符的一个集合。比如“中文”就是一个字符集,不过这样描述一个字符集并不准确。想要更精确一点,我们可以说,“第一版《新华字典》里面出现的所有汉字”,这是一个字符集。这样,我们才能明确知道,一个字符在不在这个集合里面。比如,我们日常说的 Unicode,其实就是一个字符集,包含了 150 种语言的 14 万个不同的字符。
而字符编码则是对于字符集里的这些字符,怎么一一用二进制表示出来的一个字典。我们上面说的 Unicode,就可以用 UTF-8、UTF-16,乃至 UTF-32 来进行编码,存储成二进制。所以,有了 Unicode,其实我们可以用不止 UTF-8 一种编码形式,我们也可以自己发明一套 GT-32 编码,比如就叫作 Geek Time 32 好了。只要别人知道这套编码规则,就可以正常传输、显示这段代码。

同样的文本,采用不同的编码存储下来。如果另外一个程序,用一种不同的编码方式来进行解码和展示,就会出现乱码。这就好像两个军队用密语通信,如果用错了密码本,那看到的消息就会不知所云。在中文世界里,最典型的就是“手持两把锟斤拷,口中疾呼烫烫烫”的典故。
既然今天要彻底搞清楚编码知识,我们就来弄清楚“锟斤拷”和“烫烫烫”的来龙去脉。

首先,“锟斤拷”的来源是这样的。如果我们想要用 Unicode 编码记录一些文本,特别是一些遗留的老字符集内的文本,但是这些字符在 Unicode 中可能并不存在。于是,Unicode 会统一把这些字符记录为 U+FFFD 这个编码。
如果用 UTF-8 的格式存储下来,就是\xef\xbf\xbd。如果连续两个这样的字符放在一起,\xef\xbf\xbd\xef\xbf\xbd,这个时候,如果程序把这个字符,用 GB2312 的方式进行 decode,就会变成“锟斤拷”。这就好比我们用 GB2312 这本密码本,去解密别人用 UTF-8 加密的信息,自然没办法读出有用的信息。
而“烫烫烫”,则是因为如果你用了 Visual Studio 的调试器,默认使用 MBCS 字符集。“烫”在里面是由 0xCCCC 来表示的,而 0xCC 又恰好是未初始化的内存的赋值。于是,在读到没有赋值的内存地址或者变量的时候,电脑就开始大叫“烫烫烫”了。
了解了这些原理,相信你未来在遇到中文的编码问题的时候,可以做到“手中有粮,心中不慌”了。
理解电路
电报
电报机本质上就是一个“蜂鸣器 + 长长的电线 + 按钮开关”。蜂鸣器装在接收方手里,开关留在发送方手里。双方用长长的电线连在一起。当按钮开关按下的时候,电线的电路接通了,蜂鸣器就会响。短促地按下,就是一个短促的点信号;按的时间稍微长一些,就是一个稍长的划信号。

继电器
有了电报机,只要铺设好电报线路,就可以传输我们需要的讯息了。但是这里面又出现了一个新的挑战,就是随着电线的线路越长,电线的电阻就越大。当电阻很大,而电压不够的时候,即使你按下开关,蜂鸣器也不会响。
你可能要说了,我们可以提高电压或者用更粗的电线,使得电阻更小,这样就可以让整个线路铺得更长一些。但是这个再长,也没办法从北京铺设到上海吧。要想从北京把电报发到上海,我们还得想些别的办法。
对于电报来说,电线太长了,使得线路接通也没有办法让蜂鸣器响起来。那么,我们就不要一次铺太长的线路,而把一小段距离当成一个线路,也和驿站建立一个小电报站。我们在小电报站里面安排一个电报员,他听到上一个小电报站发来的信息,然后原样输入,发到下一个电报站去。这样,我们的信号就可以一段段传输下去,而不会因为距离太长,导致电阻太大,没有办法成功传输信号。为了能够实现这样接力传输信号,在电路里面,工程师们造了一个叫作继电器(Relay)的设备。
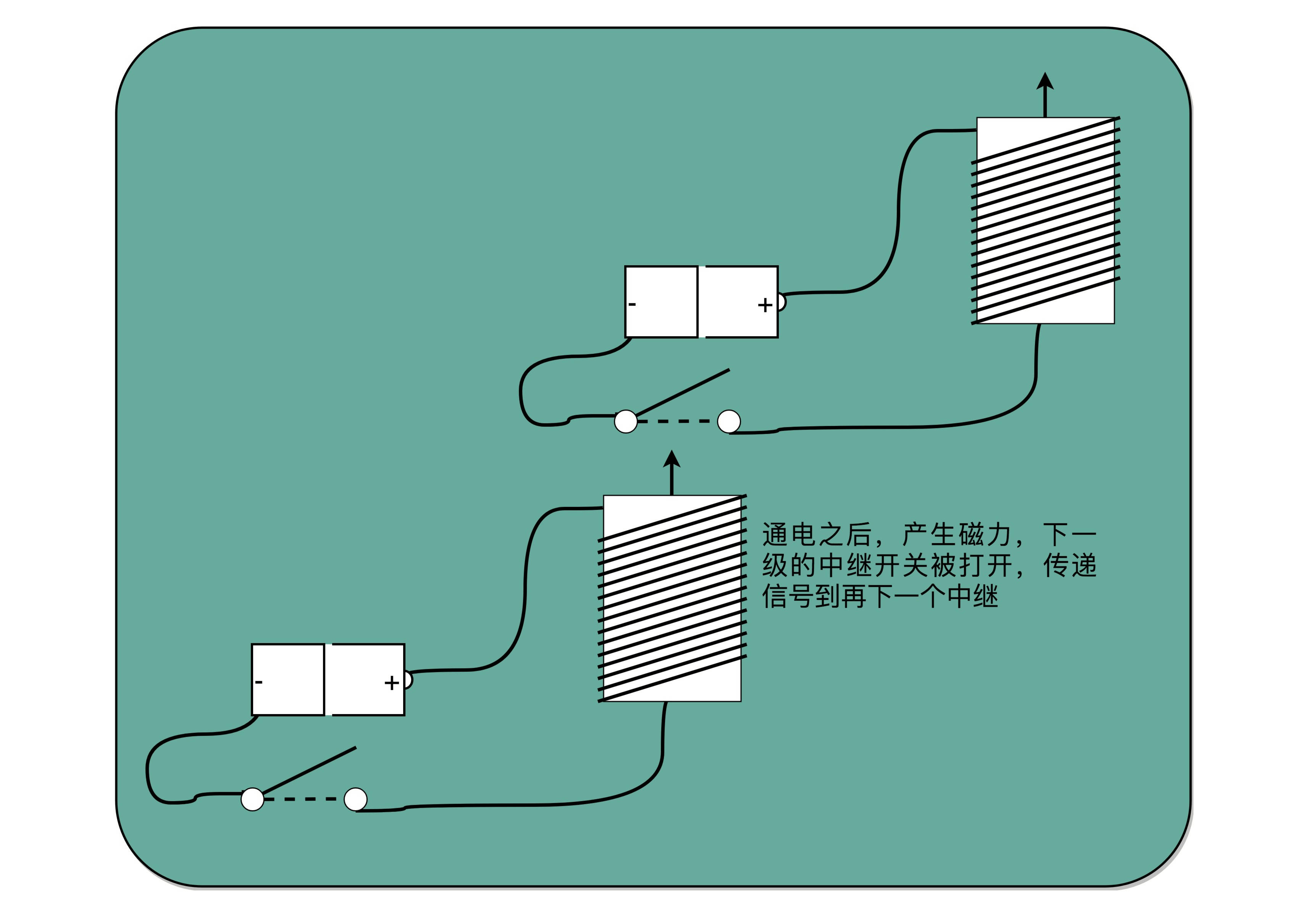
事实上,这个过程中,我们需要在每一阶段原样传输信号,所以你可以想想,我们是不是可以设计一个设备来代替这个电报员?相比使用人工听蜂鸣器的声音,来重复输入信号,利用电磁效应和磁铁,来实现这个事情会更容易。
我们把原先用来输出声音的蜂鸣器,换成一段环形的螺旋线圈,让电路封闭通上电。因为电磁效应,这段螺旋线圈会产生一个带有磁性的电磁场。我们原本需要输入的按钮开关,就可以用一块磁力稍弱的磁铁把它设在“关”的状态。这样,按下上一个电报站的开关,螺旋线圈通电产生了磁场之后,磁力就会把开关“吸”下来,接通到下一个电报站的电路。
如果我们在中间所有小电报站都用这个“螺旋线圈 + 磁性开关”的方式,来替代蜂鸣器和普通开关,而只在电报的始发和终点用普通的开关和蜂鸣器,我们就有了一个拆成一段一段的电报线路,接力传输电报信号。这样,我们就不需要中间安排人力来听打电报内容,也不需要解决因为线缆太长导致的电阻太大或者电压不足的问题了。我们只要在终点站安排电报员,听写最终的电报内容就可以了。这样是不是比之前更省事了?
事实上,继电器还有一个名字就叫作电驿,这个“驿”就是驿站的驿,可以说非常形象了。这个接力的策略不仅可以用在电报中,在通信类的科技产品中其实都可以用到。
比如说,你在家里用 WiFi,如果你的屋子比较大,可能某些房间的信号就不好。你可以选用支持“中继”的 WiFi 路由器,在信号衰减的地方,增加一个 WiFi 设备,接收原来的 WiFi 信号,再重新从当前节点传输出去。这种中继对应的英文名词和继电器是一样的,也叫 Relay。
再比如说,我们现在互联网使用的光缆,是用光信号来传输数据。随着距离的增长、反射次数的增加,信号也会有所衰减,我们同样要每隔一段距离,来增加一个用来重新放大信号的中继。
有了继电器之后,我们不仅有了一个能够接力传输信号的方式,更重要的是,和输入端通过开关的“开”和“关”来表示“1”和“0”一样,我们在输出端也能表示“1”和“0”了。
输出端的作用,不仅仅是通过一个蜂鸣器或者灯泡,提供一个供人观察的输出信号,通过“螺旋线圈 + 磁性开关”,使得我们有“开”和“关”这两种状态,这个“开”和“关”表示的“1”和“0”,还可以作为后续线路的输入信号,让我们开始可以通过最简单的电路,来组合形成我们需要的逻辑。
通过这些线圈和开关,我们也可以很容易地创建出 “与(AND)”“或(OR)”“非(NOT)”这样的逻辑。我们在输入端的电路上,提供串联的两个开关,只有两个开关都打开,电路才接通,输出的开关也才能接通,这其实就是模拟了计算机里面的“与”操作。
我们在输入端的电路,提供两条独立的线路到输出端,两条线路上各有一个开关,那么任何一个开关打开了,到输出端的电路都是接通的,这其实就是模拟了计算机中的“或”操作。
当我们把输出端的“螺旋线圈 + 磁性开关”的组合,从默认关掉,只有通电有了磁场之后打开,换成默认是打开通电的,只有通电之后才关闭,我们就得到了一个计算机中的“非”操作。输出端开和关正好和输入端相反。这个在数字电路中,也叫作反向器(Inverter)。

与、或、非的电路都非常简单,要想做稍微复杂一点的工作,我们需要很多电路的组合。不过,这也彰显了现代计算机体系中一个重要的思想,就是通过分层和组合,逐步搭建起更加强大的功能。
回到我们前面看的电报机原型,虽然一个按钮开关的电报机很“容易”操作,但是却不“方便”操作。因为电报员要熟记每一个字母对应的摩尔斯电码,并且需要快速按键来进行输入。一旦输错很难纠正。但是,因为电路之间可以通过与、或、非组合完成更复杂的功能,我们完全可以设计一个和打字机一样的电报机,每按下一个字母按钮,就会接通一部分电路,然后把这个字母的摩尔斯电码输出出去。
虽然在电报机时代,我们没有这么做,但是在计算机时代,我们其实就是这样做的。我们不再是给计算机“0”和“1”,而是通过千万个晶体管组合在一起,最终使得我们可以用“高级语言”,指挥计算机去干什么。
加法器
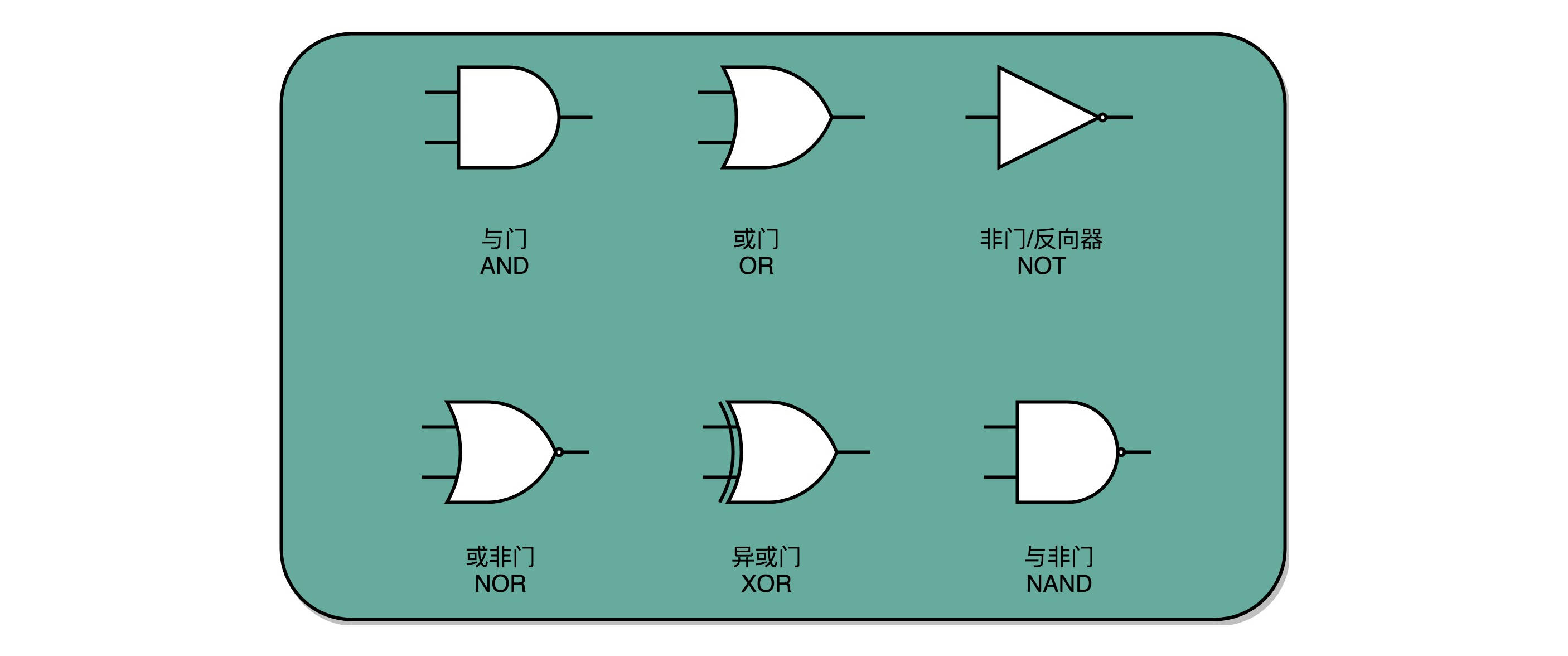
这些基本的门电路,是我们计算机硬件端的最基本的“积木”
异或门和半加器
我们看到的基础门电路,输入都是两个单独的 bit,输出是一个单独的 bit。如果我们要对 2 个 8 位(bit)的数,计算与、或、非这样的简单逻辑运算,其实很容易。只要连续摆放 8 个开关,来代表一个 8 位数。这样的两组开关,从左到右,上下单个的位开关之间,都统一用“与门”或者“或门”连起来,就是两个 8 位数的 AND 或者 OR 的运算了。
比起 AND 或者 OR 这样的电路外,要想实现整数的加法,就需要组建稍微复杂一点儿的电路了。
我们先回归一个最简单的 8 位的无符号整数的加法。这里的“无符号”,表示我们并不需要使用补码来表示负数。无论高位是“0”还是“1”,这个整数都是一个正数。
我们很直观就可以想到,要表示一个 8 位数的整数,简单地用 8 个 bit,也就是 8 个像上一讲的电路开关就好了。那 2 个 8 位整数的加法,就是 2 排 8 个开关。加法得到的结果也是一个 8 位的整数,所以又需要 1 排 8 位的开关。要想实现加法,我们就要看一下,通过什么样的门电路,能够连接起加数和被加数,得到最后期望的和。
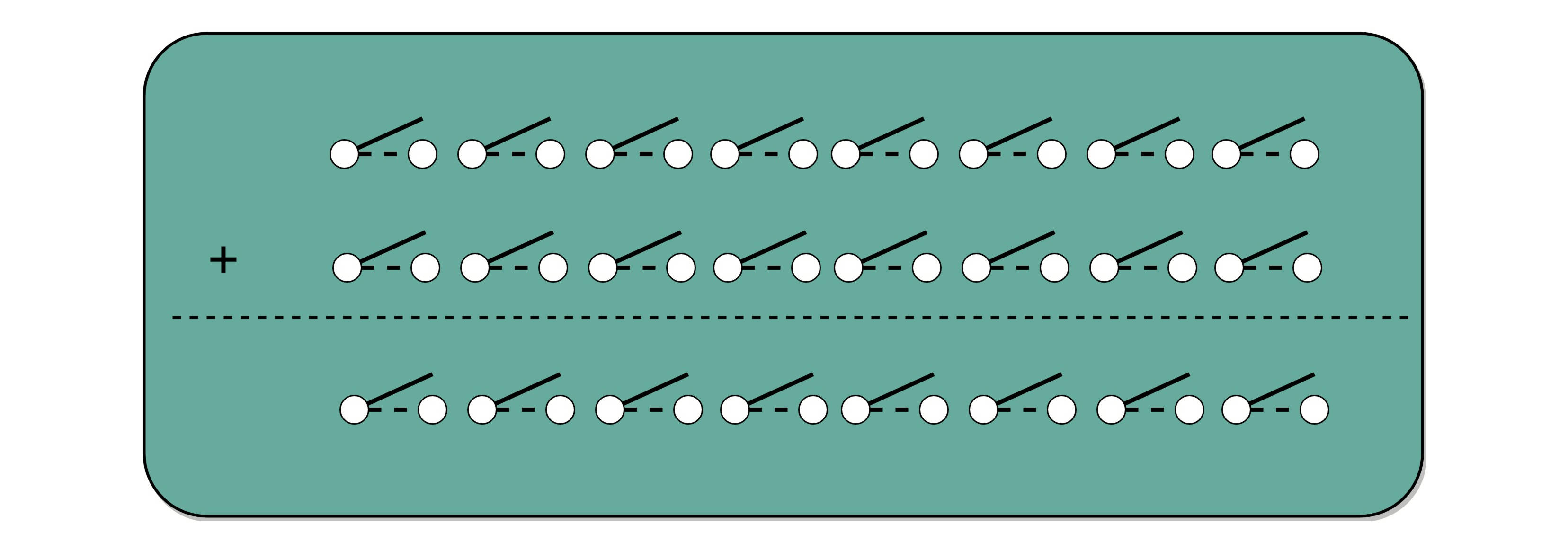
要做到这一点,我们先来看看,我们人在计算加法的时候一般会怎么操作。二进制的加法和十进制没什么区别,所以我们一样可以用列竖式来计算。我们仍然是从左到右,一位一位进行计算,只是把从逢 10 进 1 变成逢 2 进 1。
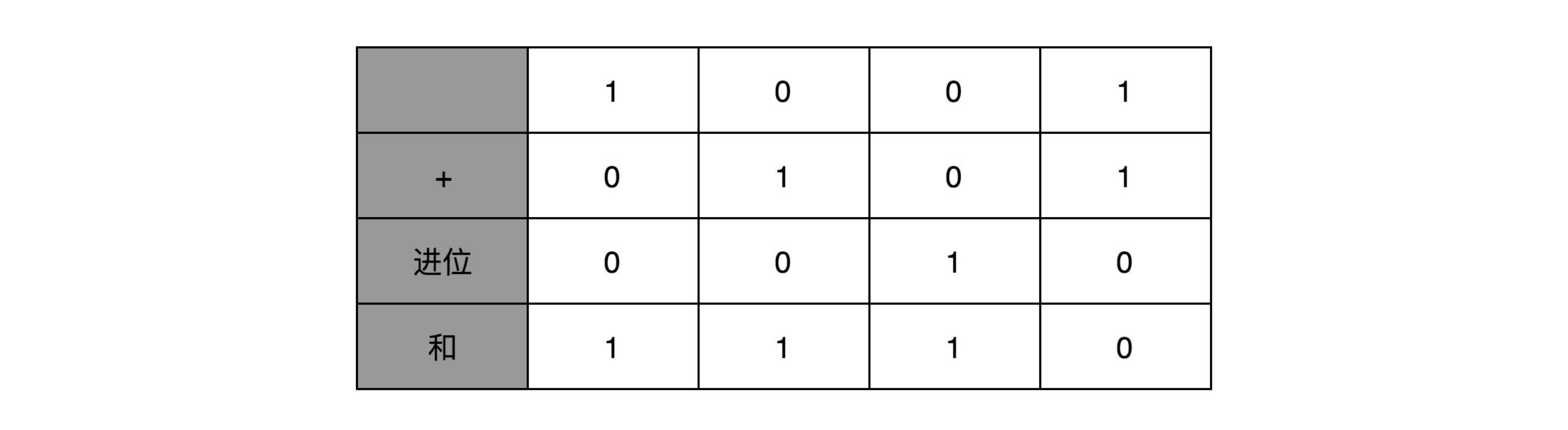
你会发现,其实计算一位数的加法很简单。我们先就看最简单的个位数。输入一共是 4 种组合,00、01、10、11。得到的结果,也不复杂。
一方面,我们需要知道,加法计算之后的个位是什么,在输入的两位是 00 和 11 的情况下,对应的输出都应该是 0;在输入的两位是 10 和 01 的情况下,输出都是 1。结果你会发现,这个输入和输出的对应关系,其实就是“异或门(XOR)”。
讲与、或、非门的时候,我们很容易就能和程序里面的“AND(通常是 & 符号)”“ OR(通常是 | 符号)”和“ NOT(通常是 ! 符号)”对应起来。可能你没有想过,为什么我们会需要“异或(XOR)”,这样一个在逻辑运算里面没有出现的形式,作为一个基本电路。其实,异或门就是一个最简单的整数加法,所需要使用的基本门电路。
算完个位的输出还不算完,输入的两位都是 11 的时候,我们还需要向更左侧的一位进行进位。那这个就对应一个与门,也就是有且只有在加数和被加数都是 1 的时候,我们的进位才会是 1。
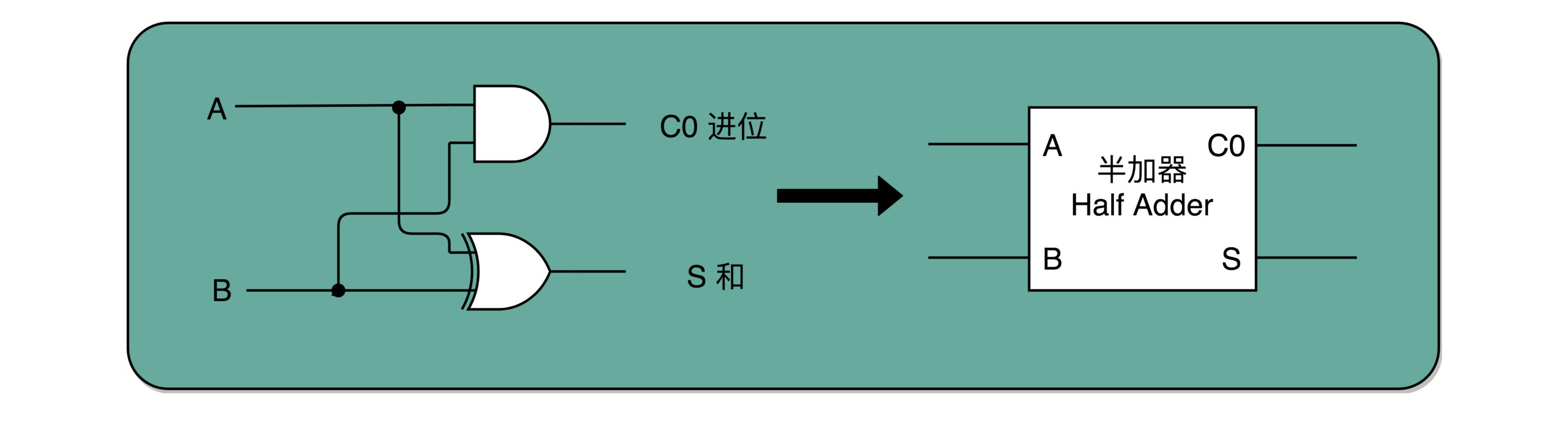
所以,通过一个异或门计算出个位,通过一个与门计算出是否进位,我们就通过电路算出了一个一位数的加法。于是,我们把两个门电路打包,给它取一个名字,就叫作半加器(Half Adder)。
全加器
半加器可以解决个位的加法问题,但是如果放到二位上来说,就不够用了。我们这里的竖式是个二进制的加法,所以如果从右往左数,第二列不是十位,我称之为“二位”。对应的再往左,就应该分别是四位、八位。
二位用一个半加器不能计算完成的原因也很简单。因为二位除了一个加数和被加数之外,还需要加上来自个位的进位信号,一共需要三个数进行相加,才能得到结果。但是我们目前用到的,无论是最简单的门电路,还是用两个门电路组合而成的半加器,输入都只能是两个 bit,也就是两个开关。那我们该怎么办呢?
实际上,解决方案也并不复杂。我们用两个半加器和一个或门,就能组合成一个全加器。第一个半加器,我们用和个位的加法一样的方式,得到是否进位 X 和对应的二个数加和后的结果 Y,这样两个输出。然后,我们把这个加和后的结果 Y,和个位数相加后输出的进位信息 U,再连接到一个半加器上,就会再拿到一个是否进位的信号 V 和对应的加和后的结果 W。
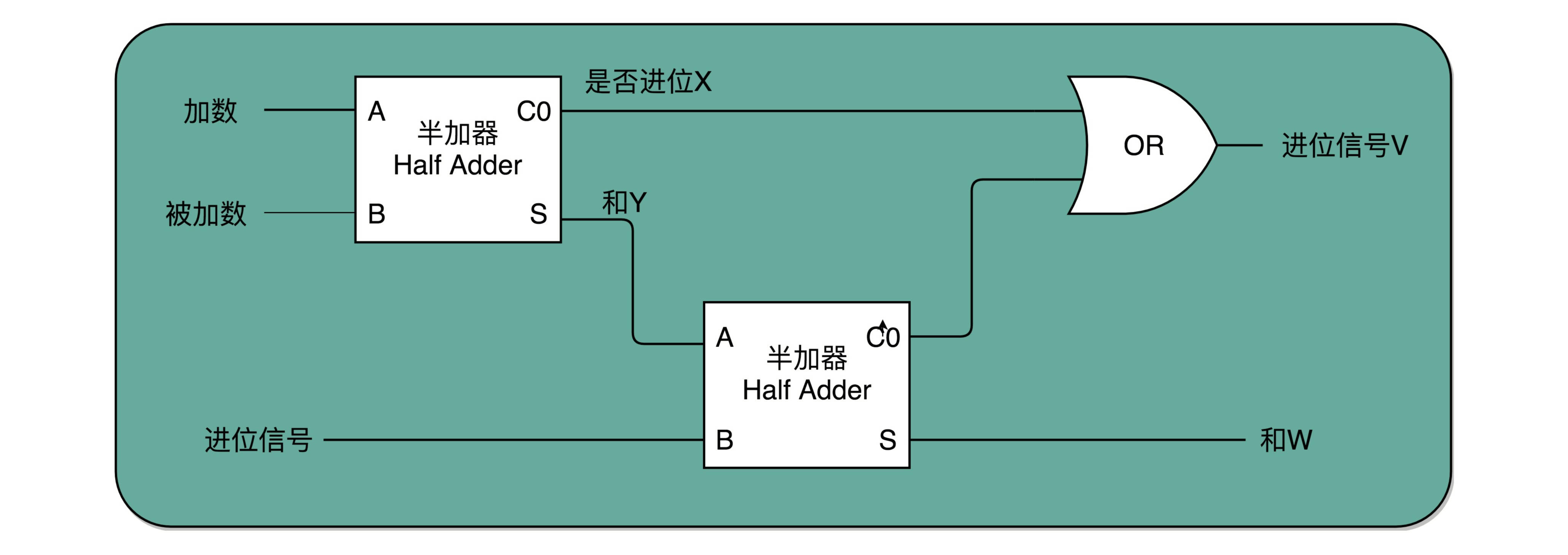
这个 W 就是我们在二位上留下的结果。我们把两个半加器的进位输出,作为一个或门的输入连接起来,只要两次加法中任何一次需要进位,那么在二位上,我们就会向左侧的四位进一位。因为一共只有三个 bit 相加,即使 3 个 bit 都是 1,也最多会进一位。
这样,通过两个半加器和一个或门,我们就得到了一个,能够接受进位信号、加数和被加数,这样三个数组成的加法。这就是我们需要的全加器。
有了全加器,我们要进行对应的两个 8 bit 数的加法就很容易了。我们只要把 8 个全加器串联起来就好了。个位的全加器的进位信号作为二位全加器的输入信号,二位全加器的进位信号再作为四位的全加器的进位信号。这样一层层串接八层,我们就得到了一个支持 8 位数加法的算术单元。如果要扩展到 16 位、32 位,乃至 64 位,都只需要多串联几个输入位和全加器就好了。
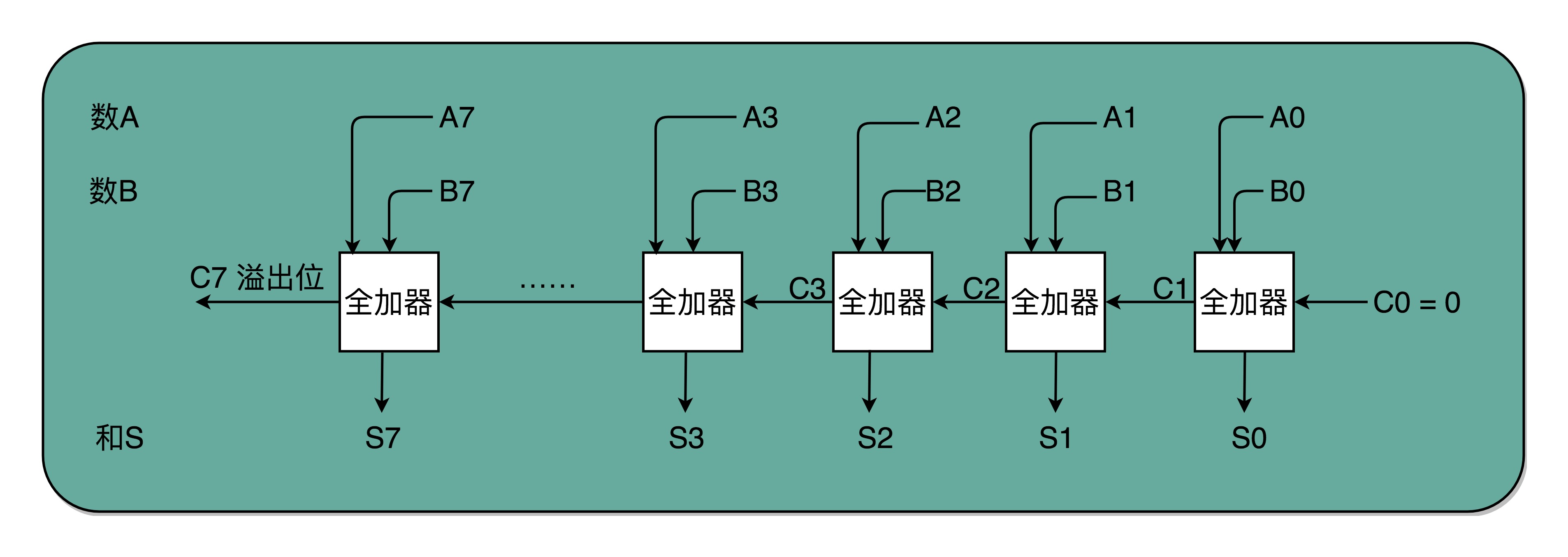
唯一需要注意的是,对于这个全加器,在个位,我们只需要用一个半加器,或者让全加器的进位输入始终是 0。因为个位没有来自更右侧的进位。而最左侧的一位输出的进位信号,表示的并不是再进一位,而是表示我们的加法是否溢出了。
看到全加器的电路设计,相信你应该明白,在整个加法器的结果中,我们其实有一个电路的信号,会标识出加法的结果是否溢出。我们可以把这个对应的信号,输出给到硬件中其他标志位里,让我们的计算机知道计算的结果是否溢出。而现代计算机也正是这样做的。这就是为什么你在撰写程序的时候,能够知道你的计算结果是否溢出在硬件层面得到的支持。
总结
通过门电路来搭建算术计算的一个小功能,就好像搭乐高积木一样。
我们用两个门电路,搭出一个半加器,就好像我们拿两块乐高,叠在一起,变成一个长方形的乐高,这样我们就有了一个新的积木组件,柱子。我们再用两个柱子和一个长条的积木组合一下,就变成一个积木桥。然后几个积木桥串接在一起,又成了积木楼梯。
当我们想要搭建一个摩天大楼,我们需要很多很多楼梯。但是这个时候,我们已经不再关注最基础的一节楼梯是怎么用一块块积木搭建起来的。这其实就是计算机中,无论软件还是硬件中一个很重要的设计思想,分层。
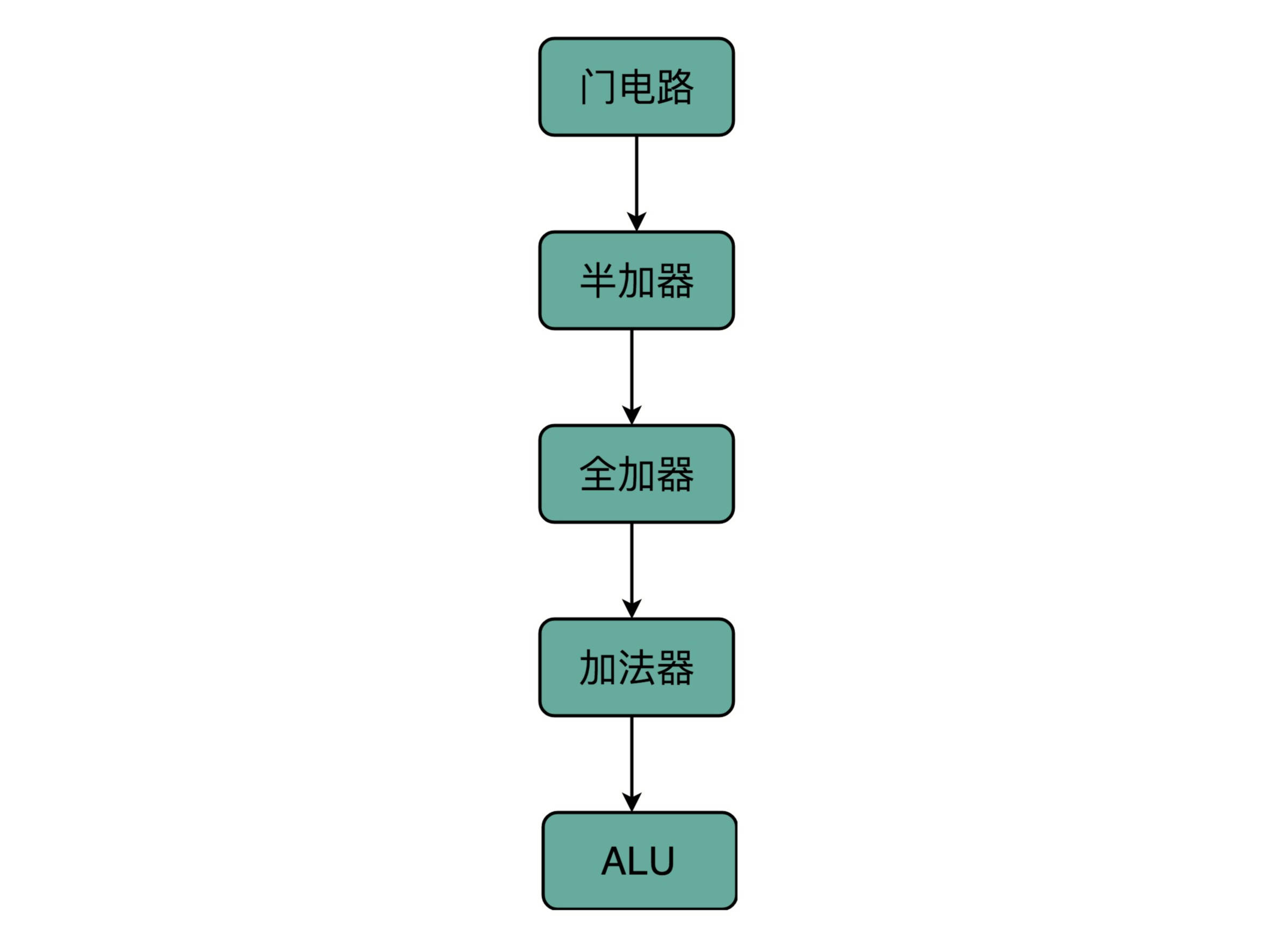
从简单到复杂,我们一层层搭出了拥有更强能力的功能组件。在上面的一层,我们只需要考虑怎么用下一层的组件搭建出自己的功能,而不需要下沉到更低层的其他组件。就像你之前并没有深入学习过计算机组成原理,一样可以直接通过高级语言撰写代码,实现功能。
在硬件层面,我们通过门电路、半加器、全加器一层层搭出了加法器这样的功能组件。我们把这些用来做算术逻辑计算的组件叫作 ALU,也就是算术逻辑单元。当进一步打造强大的 CPU 时,我们不会再去关注最细颗粒的门电路,只需要把门电路组合而成的 ALU,当成一个能够完成基础计算的黑盒子就可以了。
乘法器
十进制中的 13 乘以 9,计算的结果应该是 117。我们通过转换成二进制,然后列竖式的办法,来看看整个计算的过程是怎样的。

顺序乘法的实现过程
从列出竖式的过程中,你会发现,二进制的乘法有个很大的优点,就是这个过程你不需要背九九乘法口诀表了。因为单个位置上,乘数只能是 0 或者 1,所以实际的乘法,就退化成了位移和加法。
在 13×9 这个例子里面,被乘数 13 表示成二进制是 1101,乘数 9 在二进制里面是 1001。最右边的个位是 1,所以个位乘以被乘数,就是把被乘数 1101 复制下来。因为二位和四位都是 0,所以乘以被乘数都是 0,那么保留下来的都是 0000。乘数的八位是 1,我们仍然需要把被乘数 1101 复制下来。不过这里和个位位置的单纯复制有一点小小的差别,那就是要把复制好的结果向左侧移三位,然后把四位单独进行乘法加位移的结果,再加起来,我们就得到了最终的计算结果。
对应到我们之前讲的数字电路和 ALU,你可以看到,最后一步的加法,我们可以用上一讲的加法器来实现。乘法因为只有“0”和“1”两种情况,所以可以做成输入输出都是 4 个开关,中间用 1 个开关,同时来控制这 8 个开关的方式,这就实现了二进制下的单位的乘法。
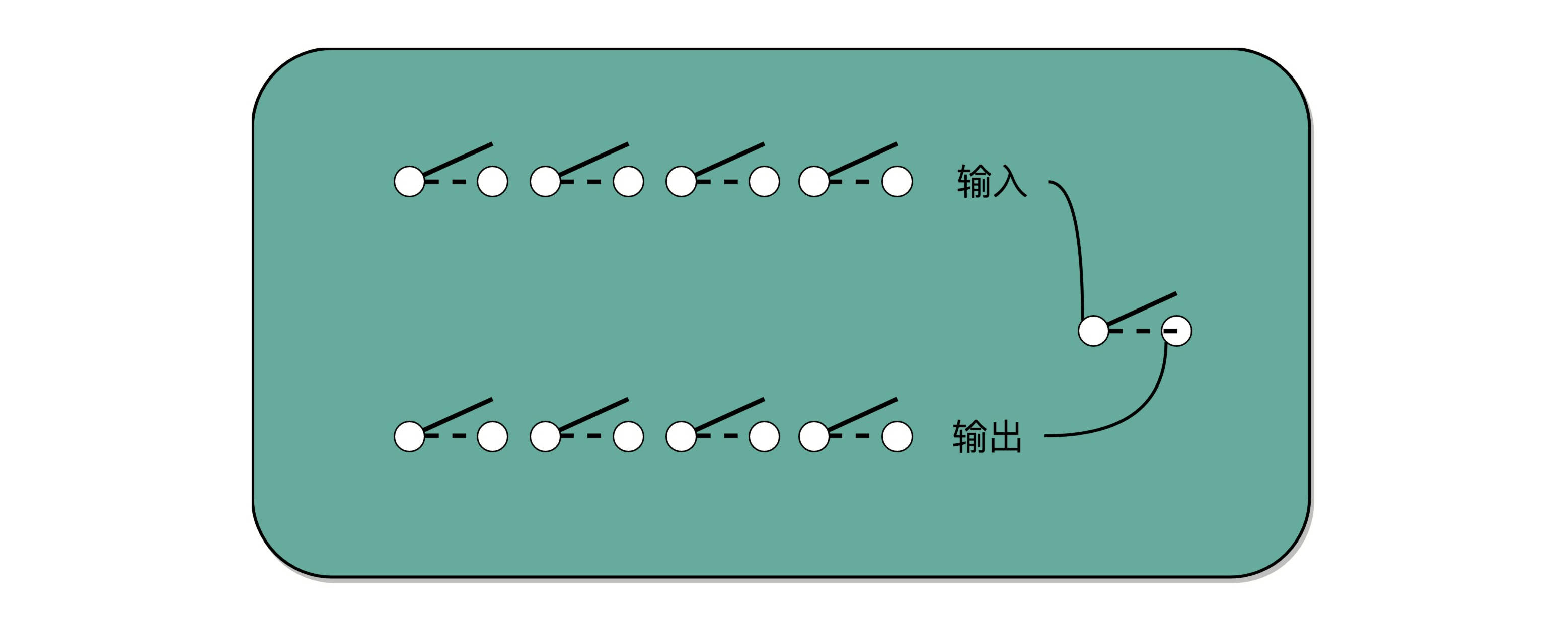
至于位移也不麻烦,我们只要不是直接连线,把正对着的开关之间进行接通,而是斜着错开位置去接就好了。如果要左移一位,就错开一位接线;如果要左移两位,就错开两位接线。
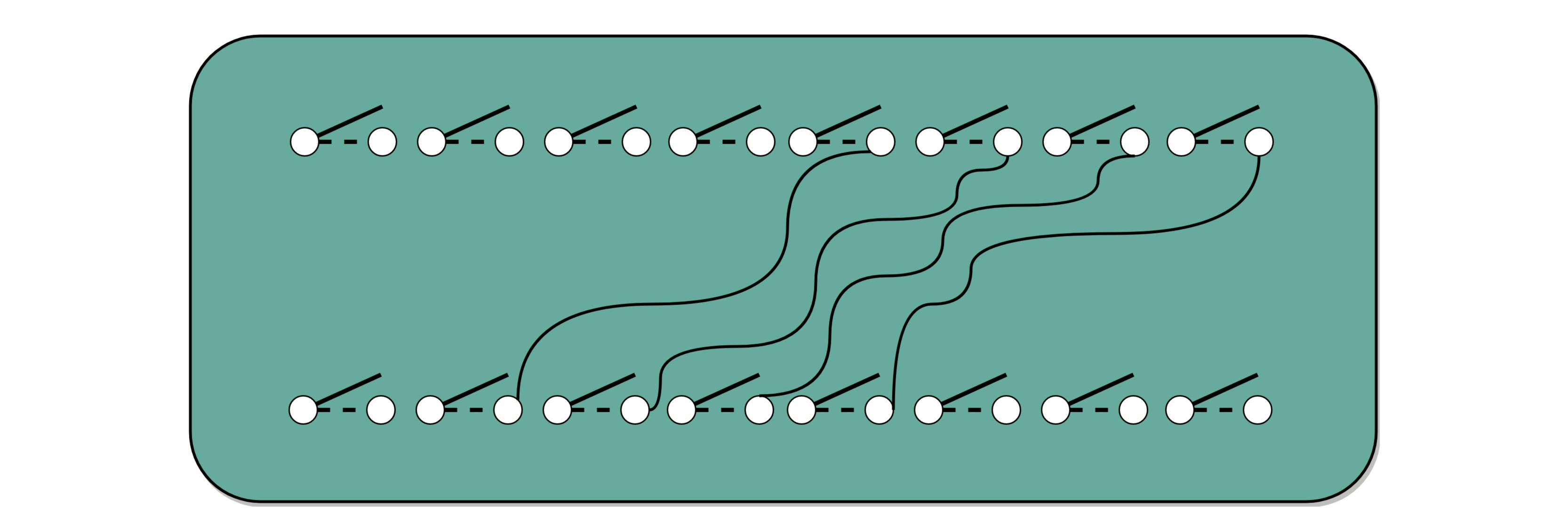
这样,你会发现,我们并不需要引入任何新的、更复杂的电路,仍然用最基础的电路,只要用不同的接线方式,就能够实现一个“列竖式”的乘法。而且,因为二进制下,只有 0 和 1,也就是开关的开和闭这两种情况,所以我们的计算机也不需要去“背诵”九九乘法口诀表,不需要单独实现一个更复杂的电路,就能够实现乘法。
为了节约一点开关,也就是晶体管的数量。实际上,像 13×9 这样两个四位数的乘法,我们不需要把四次单位乘法的结果,用四组独立的开关单独都记录下来,然后再把这四个数加起来。因为这样做,需要很多组开关,如果我们计算一个 32 位的整数乘法,就要 32 组开关,太浪费晶体管了。如果我们顺序地来计算,只需要一组开关就好了。
我们先拿乘数最右侧的个位乘以被乘数,然后把结果写入用来存放计算结果的开关里面,然后,把被乘数左移一位,把乘数右移一位,仍然用乘数去乘以被乘数,然后把结果加到刚才的结果上。反复重复这一步骤,直到不能再左移和右移位置。这样,乘数和被乘数就像两列相向而驶的列车,仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路,就能完成整个乘法。

你看这里画的乘法器硬件结构示意图。这里的控制测试,其实就是通过一个时钟信号,来控制左移、右移以及重新计算乘法和加法的时机。我们还是以计算 13×9,也就是二进制的 1101×1001 来具体看。

这个计算方式虽然节约电路了,但是也有一个很大的缺点,那就是慢。
你应该很容易就能发现,在这个乘法器的实现过程里,我们其实就是把乘法展开,变成了“加法 + 位移”来实现。我们用的是 4 位数,所以要进行 4 组“位移 + 加法”的操作。而且这 4 组操作还不能同时进行。因为下一组的加法要依赖上一组的加法后的计算结果,下一组的位移也要依赖上一组的位移的结果。这样,整个算法是“顺序”的,每一组加法或者位移的运算都需要一定的时间。
所以,最终这个乘法的计算速度,其实和我们要计算的数的位数有关。比如,这里的 4 位,就需要 4 次加法。而我们的现代 CPU 常常要用 32 位或者是 64 位来表示整数,那么对应就需要 32 次或者 64 次加法。比起 4 位数,要多花上 8 倍乃至 16 倍的时间。
换个我们在算法和数据结构中的术语来说就是,这样的一个顺序乘法器硬件进行计算的时间复杂度是 O(N)。这里的 N,就是乘法的数里面的位数。
并行加速方法
那么,我们有没有办法,把时间复杂度上降下来呢?研究数据结构和算法的时候,我们总是希望能够把 O(N) 的时间复杂度,降低到 O(logN)。办法还真的有。和软件开发里面改算法一样,在涉及 CPU 和电路的时候,我们可以改电路。
32 位数虽然是 32 次加法,但是我们可以让很多加法同时进行。回到这一讲开始,我们把位移和乘法的计算结果加到中间结果里的方法,32 位整数的乘法,其实就变成了 32 个整数相加。
前面顺序乘法器硬件的实现办法,就好像体育比赛里面的单败淘汰赛。只有一个擂台会存下最新的计算结果。每一场新的比赛就来一个新的选手,实现一次加法,实现完了剩下的还是原来那个守擂的,直到其余 31 个选手都上来比过一场。如果一场比赛需要一天,那么一共要比 31 场,也就是 31 天。
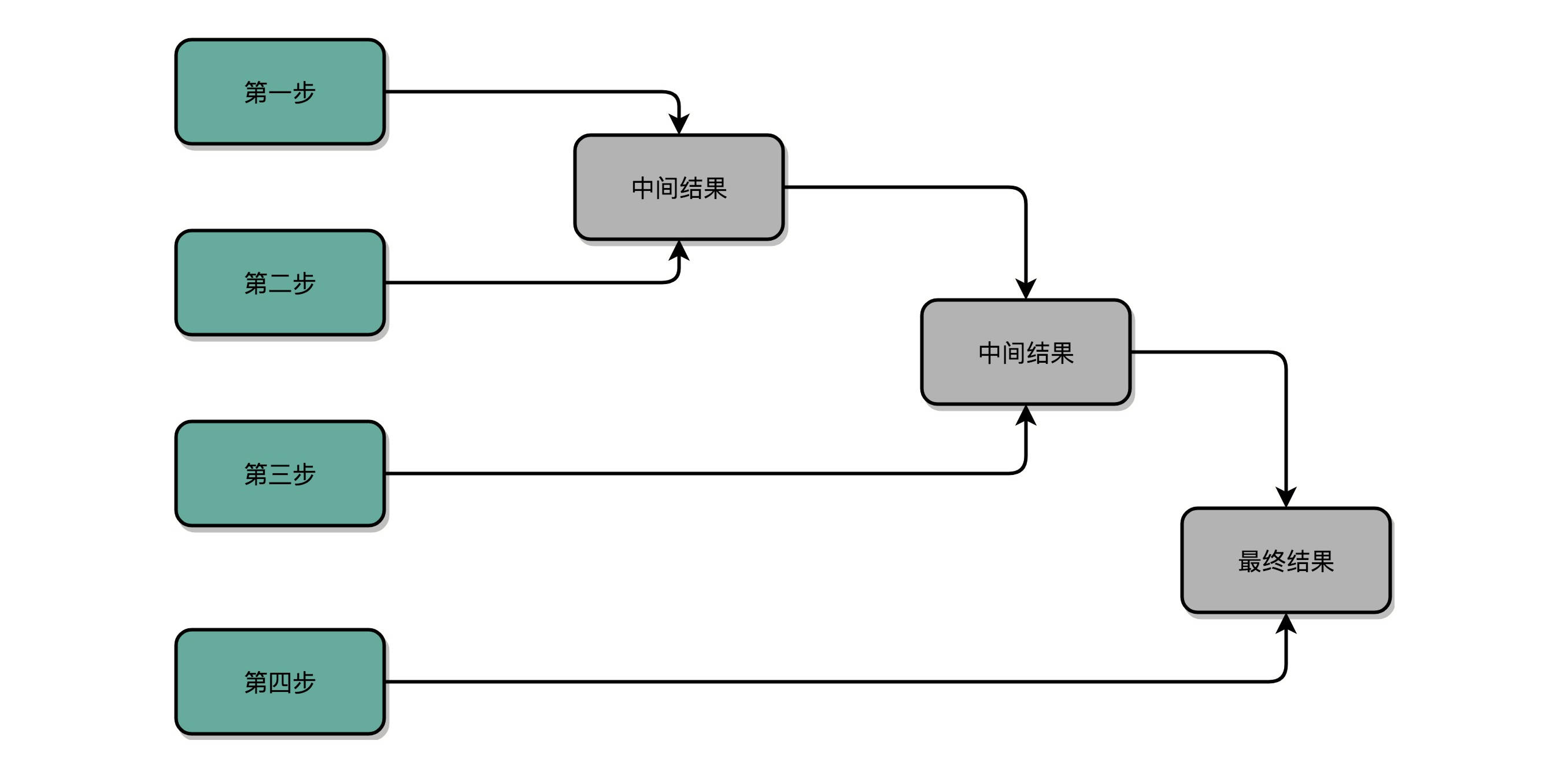
加速的办法,就是把比赛变成像世界杯足球赛那样的淘汰赛,32 个球队捉对厮杀,同时开赛。这样一天一下子就淘汰了 16 支队,也就是说,32 个数两两相加后,你可以得到 16 个结果。后面的比赛也是一样同时开赛捉对厮杀。只需要 5 天,也就是 O(log2N) 的时间,就能得到计算的结果。但是这种方式要求我们得有 16 个球场。因为在淘汰赛的第一轮,我们需要 16 场比赛同时进行。对应到我们 CPU 的硬件上,就是需要更多的晶体管开关,来放下中间计算结果。
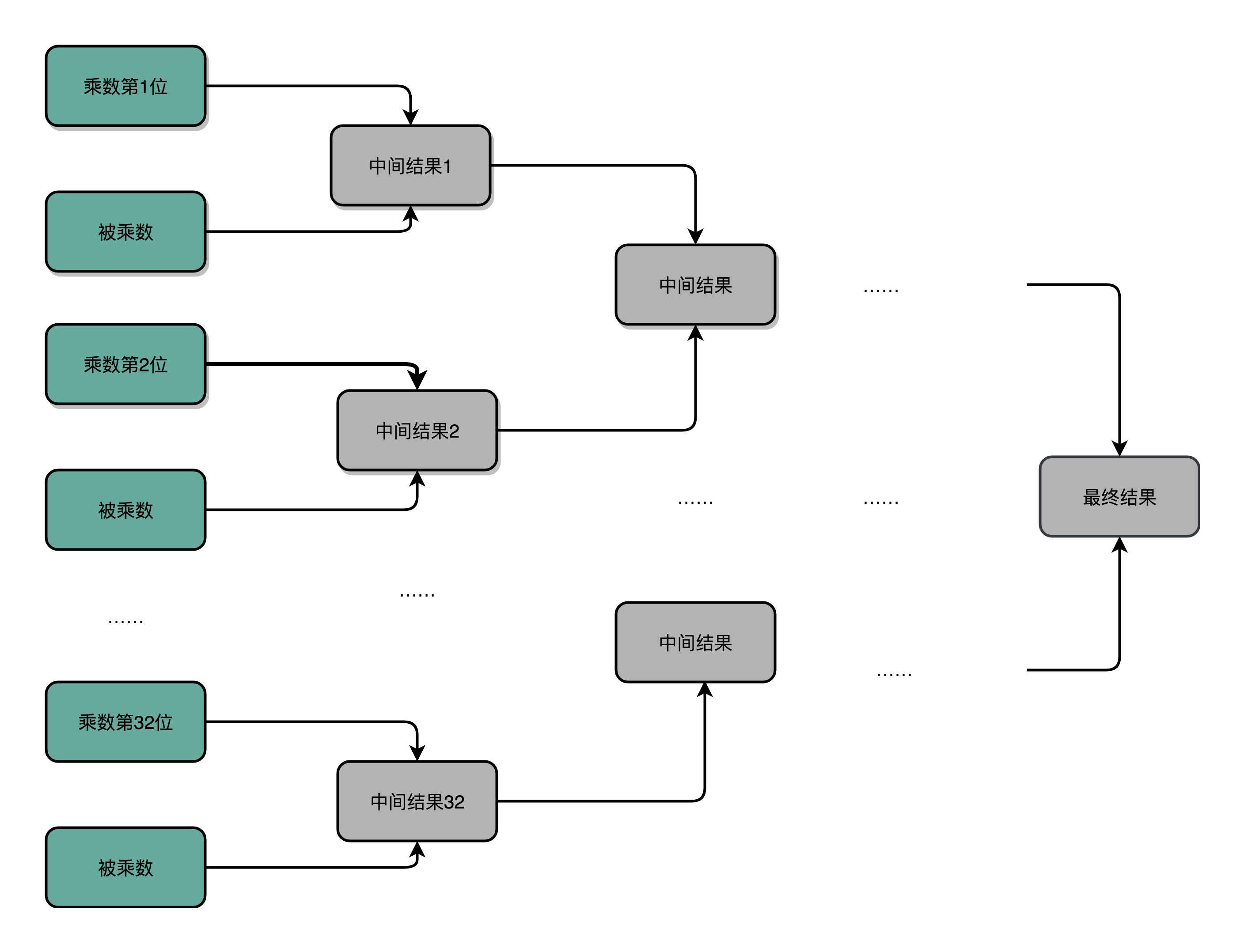
电路并行
上面我们说的并行加速的办法,看起来还是有点儿笨。我们回头来做一个抽象的思考。之所以我们的计算会慢,核心原因其实是“顺序”计算,也就是说,要等前面的计算结果完成之后,我们才能得到后面的计算结果。
最典型的例子就是我们上一讲讲的加法器。每一个全加器,都要等待上一个全加器,把对应的进入输入结果算出来,才能算下一位的输出。位数越多,越往高位走,等待前面的步骤就越多,这个等待的时间有个专门的名词,叫作门延迟(Gate Delay)。
每通过一个门电路,我们就要等待门电路的计算结果,就是一层的门电路延迟,我们一般给它取一个“T”作为符号。一个全加器,其实就已经有了 3T 的延迟(进位需要经过 3 个门电路)。而 4 位整数,最高位的计算需要等待前面三个全加器的进位结果,也就是要等 9T 的延迟。如果是 64 位整数,那就要变成 63×3=189T 的延迟。这可不是个小数字啊!
除了门延迟之外,还有一个问题就是时钟频率。在上面的顺序乘法计算里面,如果我们想要用更少的电路,计算的中间结果需要保存在寄存器里面,然后等待下一个时钟周期的到来,控制测试信号才能进行下一次移位和加法,这个延迟比上面的门延迟更可观。
那么,我们有什么办法可以解决这个问题呢?实际上,在我们进行加法的时候,如果相加的两个数是确定的,那高位是否会进位其实也是确定的。对于我们人来说,我们本身去做计算都是顺序执行的,所以要一步一步计算进位。但是,计算机是连结的各种线路。我们不用让计算机模拟人脑的思考方式,来连结线路。
那怎么才能把线路连结得复杂一点,让高位和低位的计算同时出结果呢?怎样才能让高位不需要等待低位的进位结果,而是把低位的所有输入信号都放进来,直接计算出高位的计算结果和进位结果呢?
我们只要把进位部分的电路完全展开就好了。我们的半加器到全加器,再到加法器,都是用最基础的门电路组合而成的。门电路的计算逻辑,可以像我们做数学里面的多项式乘法一样完全展开。在展开之后呢,我们可以把原来需要较少的,但是有较多层前后计算依赖关系的门电路,展开成需要较多的,但是依赖关系更少的门电路。
这里画了一个示意图,展示了一下我们加法器。如果我们完全展开电路,高位的进位和计算结果,可以和低位的计算结果同时获得。这个的核心原因是电路是天然并行的,一个输入信号,可以同时传播到所有接通的线路当中。

如果一个 4 位整数最高位是否进位,展开门电路图,你会发现,我们只需要 3T 的延迟就可以拿到是否进位的计算结果。而对于 64 位的整数,也不会增加门延迟,只是从上往下复制这个电路,接入更多的信号而已。看到没?我们通过把电路变复杂,就解决了延迟的问题。
这个优化,本质上是利用了电路天然的并行性。电路只要接通,输入的信号自动传播到了所有接通的线路里面,这其实也是硬件和软件最大的不同。
无论是这里把对应的门电路逻辑进行完全展开以减少门延迟,还是上面的乘法通过并行计算多个位的乘法,都是把我们完成一个计算的电路变复杂了。而电路变复杂了,也就意味着晶体管变多了。
之前很多同学在我们讨论计算机的性能问题的时候,都提到,为什么晶体管的数量增加可以优化计算机的计算性能。实际上,这里的门电路展开和上面的并行计算乘法都是很好的例子。我们通过更多的晶体管,就可以拿到更低的门延迟,以及用更少的时钟周期完成一个计算指令。
浮点数和定点数
浮点数的不精确性
那么,我们能不能用二进制表示所有的实数,然后在二进制下计算它的加减乘除呢?先不着急,我们从一个有意思的小案例来看。
你可以在 Linux 下打开 Python 的命令行 Console,也可以在 Chrome 浏览器里面通过开发者工具,打开浏览器里的 Console,在里面输入“0.3 + 0.6”,然后看看你会得到一个什么样的结果。
>>> 0.3 + 0.6
0.8999999999999999
不知道你有没有大吃一惊,这么简单的一个加法,无论是在 Python 还是在 JavaScript 里面,算出来的结果居然不是准确的 0.9,而是 0.8999999999999999 这么个结果。这是为什么呢?
在回答为什么之前,我们先来想一个更抽象的问题。通过前面的这么多讲,你应该知道我们现在用的计算机通常用 16/32 个比特(bit)来表示一个数。那我问你,我们用 32 个比特,能够表示所有实数吗?
答案很显然是不能。32 个比特,只能表示 2 的 32 次方个不同的数,差不多是 40 亿个。如果表示的数要超过这个数,就会有两个不同的数的二进制表示是一样的。那计算机可就会一筹莫展,不知道这个数到底是多少。
40 亿个数看似已经很多了,但是比起无限多的实数集合却只是沧海一粟。所以,这个时候,计算机的设计者们,就要面临一个问题了:我到底应该让这 40 亿个数映射到实数集合上的哪些数,在实际应用中才能最划得来呢?
定点数的表示
有一个很直观的想法,就是我们用 4 个比特来表示 0~9 的整数,那么 32 个比特就可以表示 8 个这样的整数。然后我们把最右边的 2 个 0~9 的整数,当成小数部分;把左边 6 个 0~9 的整数,当成整数部分。这样,我们就可以用 32 个比特,来表示从 0 到 999999.99 这样 1 亿个实数了。
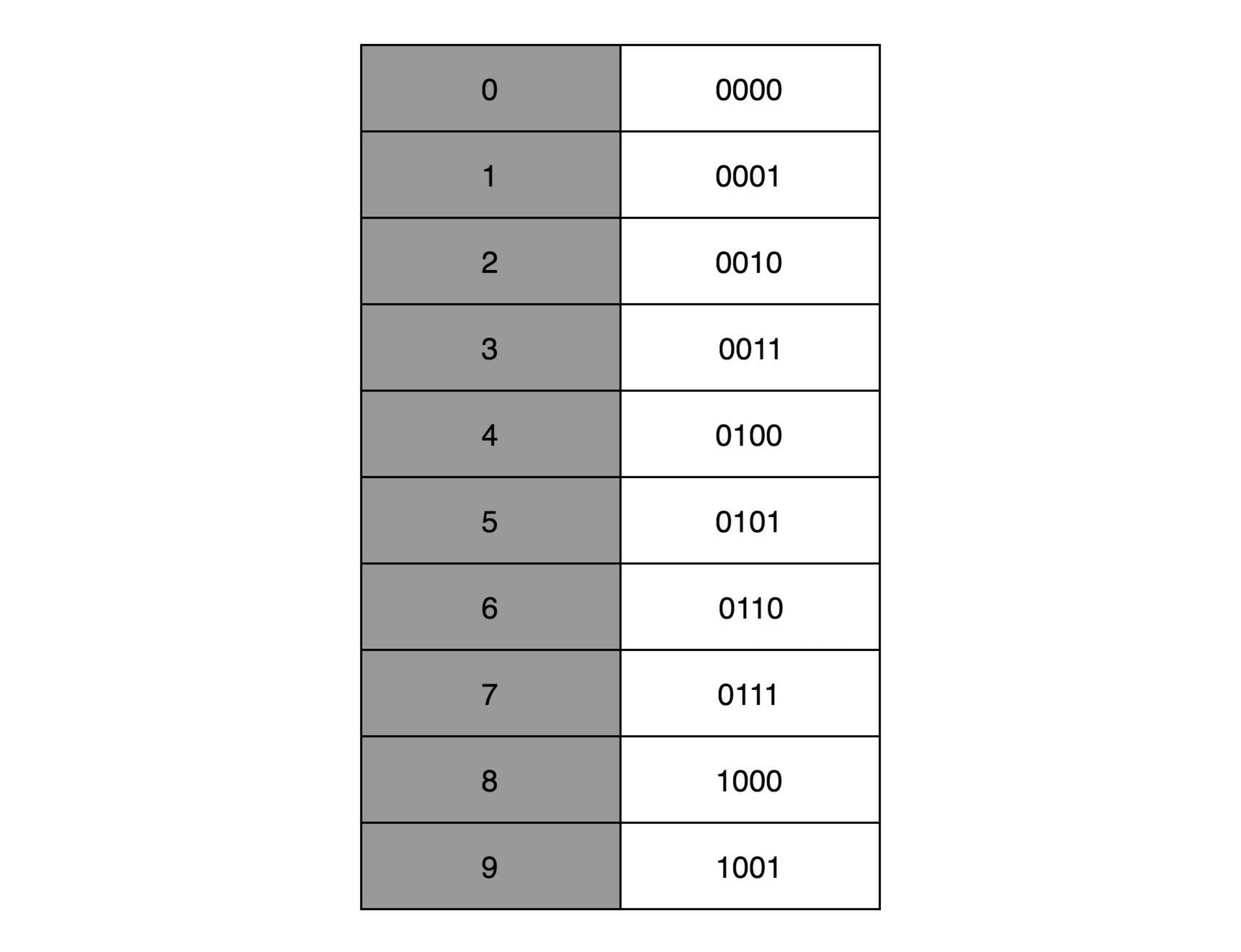
这种用二进制来表示十进制的编码方式,叫作BCD 编码(Binary-Coded Decimal)。其实它的运用非常广泛,最常用的是在超市、银行这样需要用小数记录金额的情况里。在超市里面,我们的小数最多也就到分。这样的表示方式,比较直观清楚,也满足了小数部分的计算。
不过,这样的表示方式也有几个缺点。
第一,这样的表示方式有点“浪费”。本来 32 个比特我们可以表示 40 亿个不同的数,但是在 BCD 编码下,只能表示 1 亿个数,如果我们要精确到分的话,那么能够表示的最大金额也就是到 100 万。如果我们的货币单位是人民币或者美元还好,如果我们的货币单位变成了津巴布韦币,这个数量就不太够用了。
第二,这样的表示方式没办法同时表示很大的数字和很小的数字。我们在写程序的时候,实数的用途可能是多种多样的。有时候我们想要表示商品的金额,关心的是 9.99 这样小的数字;有时候,我们又要进行物理学的运算,需要表示光速,也就是 3×1083×108 这样很大的数字。那么,我们有没有一个办法,既能够表示很小的数,又能表示很大的数呢?
浮点数的表示
答案当然是有的,就是你可能经常听说过的浮点数(Floating Point),也就是float 类型。
我们先来想一想。如果我们想在一张便签纸上,用一行来写一个十进制数,能够写下多大范围的数?因为我们要让人能够看清楚,所以字最小也有一个限制。你会发现一个和上面我们用 BCD 编码表示数一样的问题,就是纸张的宽度限制了我们能够表示的数的大小。如果宽度只放得下 8 个数字,那么我们还是只能写下最大到 99999999 这样的数字。

其实,这里的纸张宽度,就和我们 32 个比特一样,是在空间层面的限制。那么,在现实生活中,我们是怎么表示一个很大的数的呢?比如说,我们想要在一本科普书里,写一下宇宙内原子的数量,莫非是用一页纸,用好多行写下很多个 0 么?
当然不是了,我们会用科学计数法来表示这个数字。宇宙内的原子的数量,大概在 10 的 82 次方左右,我们就用 1.0×10821.0×1082 这样的形式来表示这个数值,不需要写下 82 个 0。
在计算机里,我们也可以用一样的办法,用科学计数法来表示实数。浮点数的科学计数法的表示,有一个IEEE的标准,它定义了两个基本的格式。一个是用 32 比特表示单精度的浮点数,也就是我们常常说的 float 或者 float32 类型。另外一个是用 64 比特表示双精度的浮点数,也就是我们平时说的 double 或者 float64 类型。
双精度类型和单精度类型差不多,这里,我们来看单精度类型,双精度你自然也就明白了。

单精度的 32 个比特可以分成三部分。
第一部分是一个符号位,用来表示是正数还是负数。我们一般用s来表示。在浮点数里,我们不像正数分符号数还是无符号数,所有的浮点数都是有符号的。
接下来是一个 8 个比特组成的指数位。我们一般用e来表示。8 个比特能够表示的整数空间,就是 0~255。我们在这里用 1~254 映射到 -126~127 这 254 个有正有负的数上。因为我们的浮点数,不仅仅想要表示很大的数,还希望能够表示很小的数,所以指数位也会有负数。
你发现没,我们没有用到 0 和 255。没错,这里的 0(也就是 8 个比特全部为 0) 和 255 (也就是 8 个比特全部为 1)另有它用,我们等一下再讲。
最后,是一个 23 个比特组成的有效数位。我们用f来表示。综合科学计数法,我们的浮点数就可以表示成下面这样:
你会发现,这里的浮点数,没有办法表示 0。的确,要表示 0 和一些特殊的数,我们就要用上在 e 里面留下的 0 和 255 这两个表示,这两个表示其实是两个标记位。在 e 为 0 且 f 为 0 的时候,我们就把这个浮点数认为是 0。至于其它的 e 是 0 或者 255 的特殊情况,你可以看下面这个表格,分别可以表示出无穷大、无穷小、NAN 以及一个特殊的不规范数。
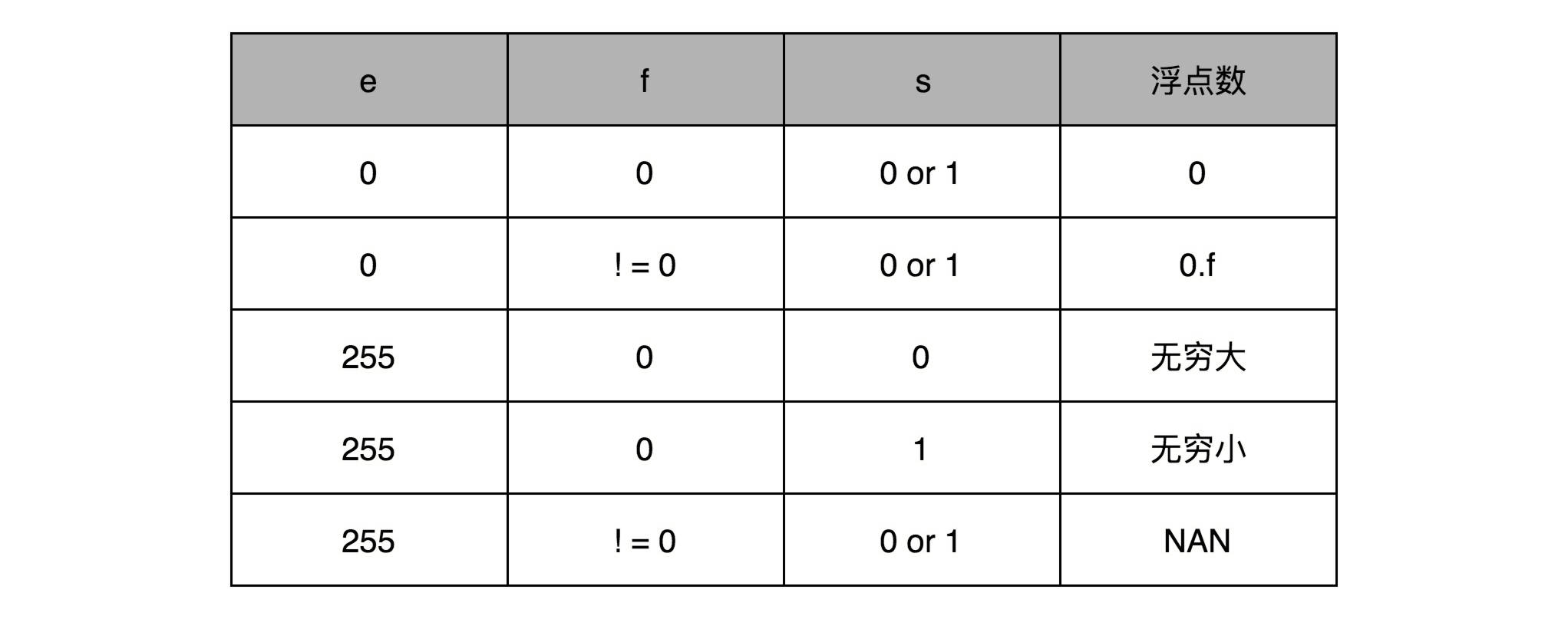
我们可以以 0.5 为例子。0.5 的符号为 s 应该是 0,f 应该是 0,而 e 应该是 -1,也就是
,对应的浮点数表示,就是 32 个比特。

,需要注意,e 表示从 -126 到 127 个,-1 是其中的第 126 个数,这里的 e 如果用整数表示,就是
。
在这样的浮点数表示下,不考虑符号的话,浮点数能够表示的最小的数和最大的数,差不多是
和
。比前面的 BCD 编码能够表示的范围大多了。
浮点数的二进制转化
我们首先来看,十进制的浮点数怎么表示成二进制。
我们输入一个任意的十进制浮点数,背后都会对应一个二进制表示。比方说,我们输入了一个十进制浮点数 9.1。那么按照之前的讲解,在二进制里面,我们应该把它变成一个“符号位 s+ 指数位 e+ 有效位数 f”的组合。第一步,我们要做的,就是把这个数变成二进制。
首先,我们把这个数的整数部分,变成一个二进制。这个我们前面讲二进制的时候已经讲过了。这里的 9,换算之后就是 1001。
接着,我们把对应的小数部分也换算成二进制。小数怎么换成二进制呢?我们先来定义一下,小数的二进制表示是怎么回事。我们拿 0.1001 这样一个二进制小数来举例说明。和上面的整数相反,我们把小数点后的每一位,都表示对应的 2 的 -N 次方。那么 0.1001,转化成十进制就是:
和整数的二进制表示采用“除以 2,然后看余数”的方式相比,小数部分转换成二进制是用一个相似的反方向操作,就是乘以 2,然后看看是否超过 1。如果超过 1,我们就记下 1,并把结果减去 1,进一步循环操作。在这里,我们就会看到,0.1 其实变成了一个无限循环的二进制小数,0.000110011。这里的“0011”会无限循环下去。
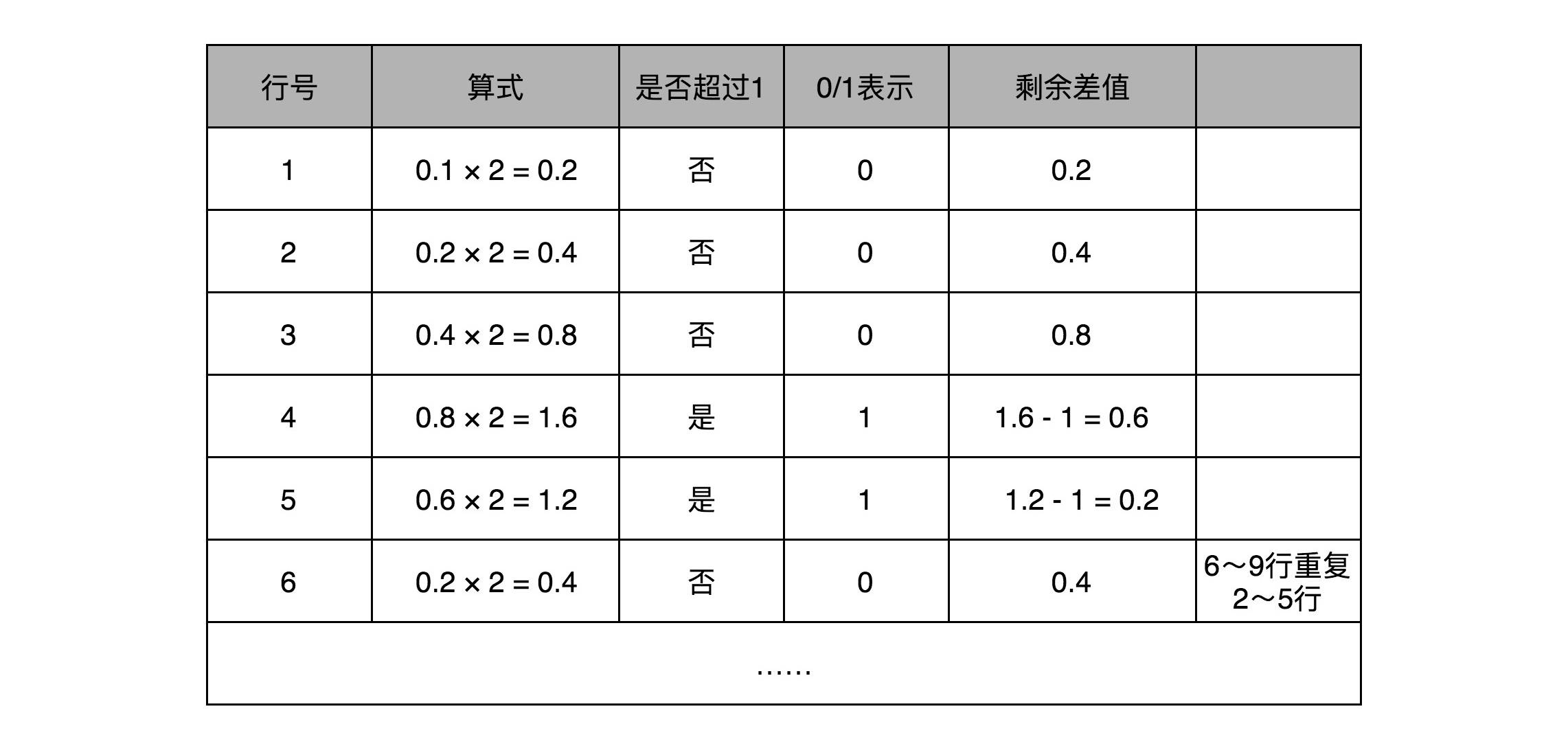
然后,我们把整数部分和小数部分拼接在一起,9.1 这个十进制数就变成了 1001.000110011…这样一个二进制表示。
上一讲我们讲过,浮点数其实是用二进制的科学计数法来表示的,所以我们可以把小数点左移三位,这个数就变成了:
那这个二进制的科学计数法表示,我们就可以对应到了浮点数的格式里了。这里的符号位 s = 0,对应的有效位 f=001000110011…。因为 f 最长只有 23 位,那这里“0011”无限循环,最多到 23 位就截止了。于是,f=00100011001100110011 001。最后的一个“0011”循环中的最后一个“1”会被截断掉。对应的指数为 e,代表的应该是 3。因为指数位有正又有负,所以指数位在 127 之前代表负数,之后代表正数,那 3 其实对应的是加上 127 的偏移量 130,转化成二进制,就是 130,对应的就是指数位的二进制,表示出来就是 10000010。

然后,我们把“s+e+f”拼在一起,就可以得到浮点数 9.1 的二进制表示了。最终得到的二进制表示就变成了:
010000010 0010 0011001100110011 001
如果我们再把这个浮点数表示换算成十进制, 实际准确的值是 9.09999942779541015625。相信你现在应该不会感觉奇怪了。
我在这里放一个链接,这里提供了直接交互式地设置符号位、指数位和有效位数的操作。你可以直观地看到,32 位浮点数每一个 bit 的变化,对应的有效位数、指数会变成什么样子以及最后的十进制的计算结果是怎样的。
浮点数的加法和精度损失
搞清楚了怎么把一个十进制的数值,转化成 IEEE-754 标准下的浮点数表示,我们现在来看一看浮点数的加法是怎么进行的。其实原理也很简单,你记住六个字就行了,那就是先对齐、再计算。
两个浮点数的指数位可能是不一样的,所以我们要把两个的指数位,变成一样的,然后只去计算有效位的加法就好了。
比如 0.5,表示成浮点数,对应的指数位是 -1,有效位是 00…(后面全是 0,记住 f 前默认有一个 1)。0.125 表示成浮点数,对应的指数位是 -3,有效位也还是 00…(后面全是 0,记住 f 前默认有一个 1)。
那我们在计算 0.5+0.125 的浮点数运算的时候,首先要把两个的指数位对齐,也就是把指数位都统一成两个其中较大的 -1。对应的有效位 1.00…也要对应右移两位,因为 f 前面有一个默认的 1,所以就会变成 0.01。然后我们计算两者相加的有效位 1.f,就变成了有效位 1.01,而指数位是 -1,这样就得到了我们想要的加法后的结果。
实现这样一个加法,也只需要位移。和整数加法类似的半加器和全加器的方法就能够实现,在电路层面,也并没有引入太多新的复杂性。
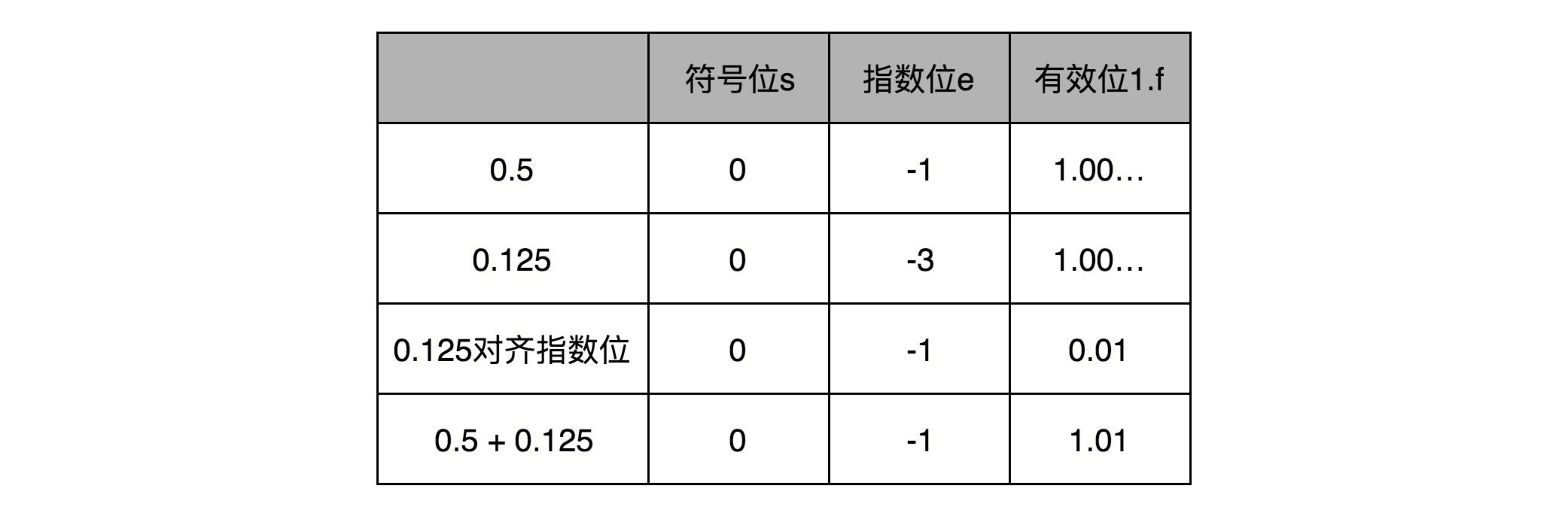
同样的,你可以用刚才那个链接来试试看,我们这个加法计算的浮点数的结果是不是正确。
回到浮点数的加法过程,你会发现,其中指数位较小的数,需要在有效位进行右移,在右移的过程中,最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数,在加法发生之前,就丢失精度。两个相加数的指数位差的越大,位移的位数越大,可能丢失的精度也就越大。当然,也有可能你的运气非常好,右移丢失的有效位都是 0。这种情况下,对应的加法虽然丢失了需要加的数字的精度,但是因为对应的值都是 0,实际的加法的数值结果不会有精度损失。
32 位浮点数的有效位长度一共只有 23 位,如果两个数的指数位差出 23 位,较小的数右移 24 位之后,所有的有效位就都丢失了。这也就意味着,虽然浮点数可以表示上到 3.40×10^38,下到 1.17×10^−38 这样的数值范围。但是在实际计算的时候,只要两个数,差出 2^24,也就是差不多 1600 万倍,那这两个数相加之后,结果完全不会变化。
你可以试一下,我下面用一个简单的 Java 程序,让一个值为 2000 万的 32 位浮点数和 1 相加,你会发现,+1 这个过程因为精度损失,被“完全抛弃”了。
public class FloatPrecision {
public static void main(String[] args) {
float a = 20000000.0f;
float b = 1.0f;
float c = a + b;
System.out.println("c is " + c);
float d = c - a;
System.out.println("d is " + d);
}
}
对应的输出结果就是:
c is 2.0E7
d is 0.0
Kahan Summation 算法
那么,我们有没有什么办法来解决这个精度丢失问题呢?虽然我们在计算浮点数的时候,常常可以容忍一定的精度损失,但是像上面那样,如果我们连续加 2000 万个 1,2000 万的数值都会被精度损失丢掉了,就会影响我们的计算结果。
一个常见的应用场景是,在一些“积少成多”的计算过程中,比如在机器学习中,我们经常要计算海量样本计算出来的梯度或者 loss,于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大,但是随着累积值的越来越大,就会出现“大数吃小数”的情况。
我们可以做一个简单的实验,用一个循环相加 2000 万个 1.0f,最终的结果会是 1600 万左右,而不是 2000 万。这是因为,加到 1600 万之后的加法因为精度丢失都没有了。这个代码比起上面的使用 2000 万来加 1.0 更具有现实意义。
public class FloatPrecision {
public static void main(String[] args) {
float sum = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
sum += x;
}
System.out.println("sum is " + sum);
}
}
对应的输出结果是:
sum is 1.6777216E7
面对这个问题,聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作Kahan Summation的算法来解决这个问题。算法的对应代码我也放在文稿中了。从中你可以看到,同样是 2000 万个 1.0f 相加,用这种算法我们得到了准确的 2000 万的结果。
public class KahanSummation {
public static void main(String[] args) {
float sum = 0.0f;
float c = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
float y = x - c;
float t = sum + y;
c = (t-sum)-y;
sum = t;
}
System.out.println("sum is " + sum);
}
}
对应的输出结果就是:
sum is 2.0E7
其实这个算法的原理其实并不复杂,就是在每次的计算过程中,都用一次减法,把当前加法计算中损失的精度记录下来,然后在后面的循环中,把这个精度损失放在要加的小数上,再做一次运算。
如果你对这个背后的数学原理特别感兴趣,可以去看一看Wikipedia 链接里面对应的数学证明,也可以生成一些数据试一试这个算法。这个方法在实际的数值计算中也是常用的,也是大量数据累加中,解决浮点数精度带来的“大数吃小数”问题的必备方案。
总结
到这里,我们已经讲完了浮点数的表示、加法计算以及可能会遇到的精度损失问题。可以看到,虽然浮点数能够表示的数据范围变大了很多,但是在实际应用的时候,由于存在精度损失,会导致加法的结果和我们的预期不同,乃至于完全没有加上的情况。
所以,一般情况下,在实践应用中,对于需要精确数值的,比如银行存款、电商交易,我们都会使用定点数或者整数类型。
比方说,你一定在 MySQL 里用过 decimal(12,2),来表示订单金额。如果我们的银行存款用 32 位浮点数表示,就会出现,马云的账户里有 2 千万,我的账户里只剩 1 块钱。结果银行一汇总总金额,那 1 块钱在账上就“不翼而飞”了。
而浮点数呢,则更适合我们不需要有一个非常精确的计算结果的情况。因为在真实的物理世界里,很多数值本来就不是精确的,我们只需要有限范围内的精度就好了。比如,从我家到办公室的距离,就不存在一个 100% 精确的值。我们可以精确到公里、米,甚至厘米,但是既没有必要、也没有可能去精确到微米乃至纳米。
对于浮点数加法中可能存在的精度损失,特别是大量加法运算中累积产生的巨大精度损失,我们可以用 Kahan Summation 这样的软件层面的算法来解决。