随机数无疑是计算机程序设计中极其重要的一个东西,无论是完成简单的抽奖小程序还是使用蒙特卡洛方法都需要使用随机数,而很多人每天都在使用随机数,却不知道随机数是怎么生成的。
平方取中法
平方取中法是我们的计算机之父冯·诺依曼提出的。此法开始取一个2s位的整数,称为种子,将其平方,得4s位整数(不足4s位时高位补0),然后取此4s位的中间2s位作为下一个种子数,并对此数规范化(即化成小于1的2s位的实数值),即为第一个(0,1)上的随机数。以此类推,即可得到一系列随机数。
它的算法公式如下
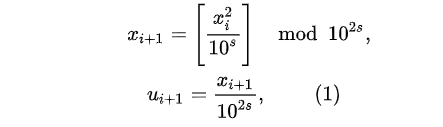
其中u代表生成的随机数,x代表种子数
我们来看看计算机之父提出的随机数算法效果如何,令s = 2,x = 6666,来输出10个数看看
public class Random{
static long s = 2;
static long x = 6666;
public static double random() {
long t = (x*x)/((long)Math.pow(10,s))%((long)Math.pow(10,2*s));
x = t;
return t*1.0/((long)Math.pow(10,2*s));
}
public static void main(String[] args) {
for(int i = 0;i<10;i++)
System.out.println(random());
}
}
输出
0.4355
0.966
0.3156
0.9603
0.2176
0.7349
0.0078
0.006
0.0036
0.0012
看起来这个算法还行,我们输出一万个数用直方图统计一下看看效果怎么样
统计结果1
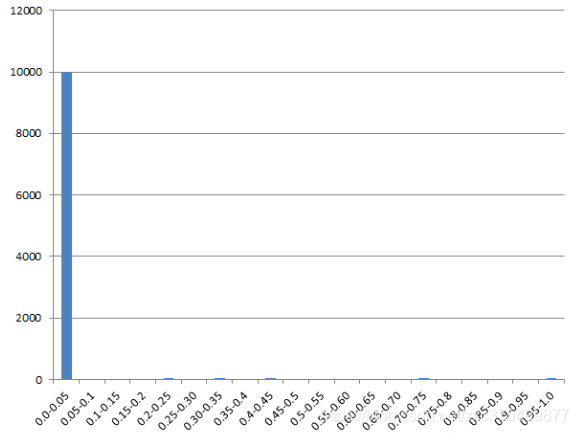
额。。。为什么看起来输出的数字全在0.0-0.05这个区间上
把所有数字输出到控制台之后,发现从第11位数字之后,输出的数字就都是0
确实,平分取中法优点是计算简单,但它有许多缺点:首先很难说明取什么样的种子值可保证有足够长的周期;其次容易退化为一常数,甚至退化为零,因为一旦有一个数为零,以后的数都将为零。
平方取中法的成功与否与种子及常数的选取关系很大,一般说来,s值很大时,种子取值也很大,可使退化推迟,周期加长
我们把s设为4,x设为66666666再统计试试看
统计结果2
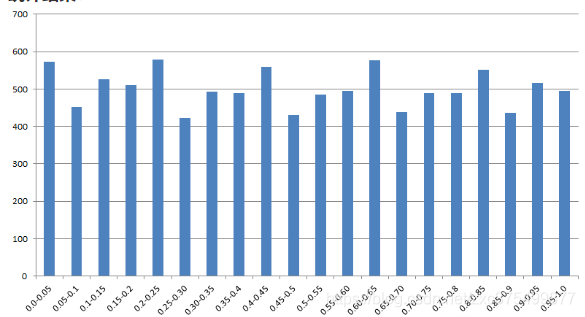
这下数字分布就比较平均了,这个算法还是有可取之处的
线性同余法
线性同余法亦称“线性同余随机数生成器”,由美国莱默尔在1951年提出,它是很常见的一种随机数生成算法。它的递推公式如下:
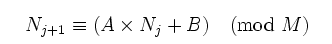
其中A,B,M是设定的常数,用线性同余法产生随机数的特点是非常容易实现,生成速度快。线性同余法的最大周期是M,要使周期达到最大,要满足以下条件:

下面我们看看线性同余法的效果
public class Random{
static int A = 97;
static int B = 3;
static int M = 10001;
static int N = 71;
public static double random() {
return (N = (N*A+B)%M)*1.0/M;
}
public static void main(String[] args) {
for(int i = 0;i<10;i++)
System.out.println(random());
}
}
输出
0.688931106889311
0.8266173382661733
0.18218178182181782
0.6719328067193281
0.1777822217778222
0.24517548245175483
0.7823217678232177
0.8855114488551145
0.8949105089491051
0.8066193380661933
再输出一万个数统计试试
统计结果
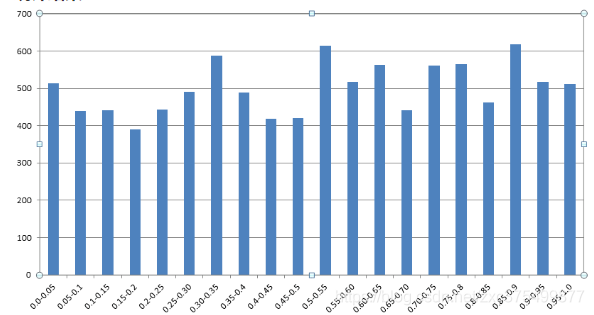
效果也很不错
其他的随机数生成方法还有很多,例如XorShift算法通过异或和位移实现 , 每次生成不同的32位, 周期为2的32次方减1,也很简单高效
欢迎关注微信公众号:Java后台开发
致力于分享原创计算机与软件开发知识及SSM、Spring cloud、Redis、微服务等Java后端开发技术
公众号里还有很多开发工具及学习资料

