Luogu P3990 [SHOI2013]超级跳马

这道题还是一道比较不可做的矩阵题

首先我们先YY一个递推的算法：令f[i][j]表示走到第i行第j列时的方案数，那么有以下转移：

f[i][j]=f[i-1][j-2*k+1]+f[i+1][j-2*k+1]+f[i][j-2*k+1](1<=k<=i/2)

但这样是很慢的，然后我们就可以前缀和优化

这里有两种方法，一个是用奇偶数行进行讨论，还有一种我认为是比较清晰的也比较容易理解

我们先来看一张图：

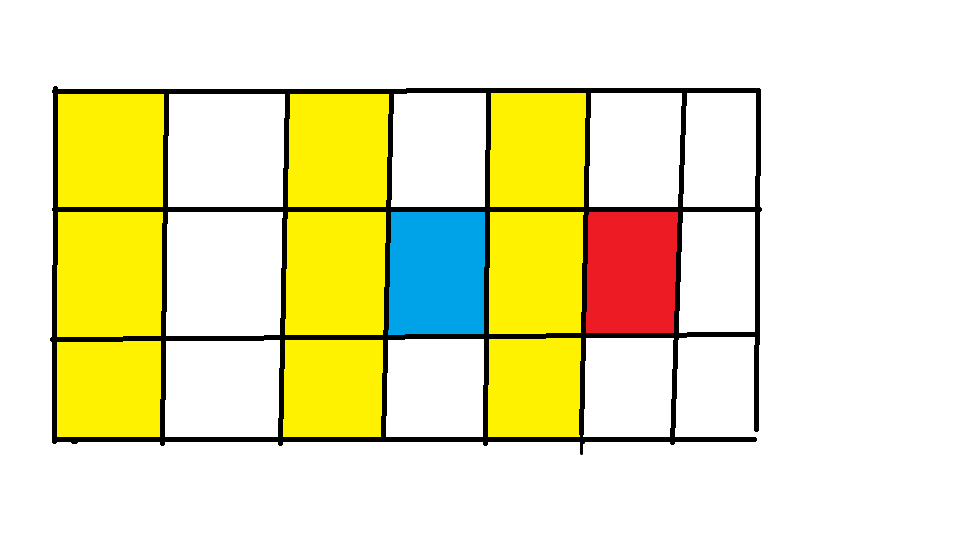
我们令f[i][j]表示前面可以转移到它的前缀和。例如图中的蓝色格子就是前6个格子的和

然后我们发现红色格子就是由蓝色格子+与它相近（i坐标差值为1）的3个黄色格子的值

然后就可以O(nm)求，但是这显然是过不了的

但是我们仔细研究一下发现每一次的转移都是等价的，所以我们用矩阵优化

由于每一列的值都和它前面两列有关，所以我们需要一个2*n*2*n的矩阵来转移，这个的话大概长这样(n=3时)

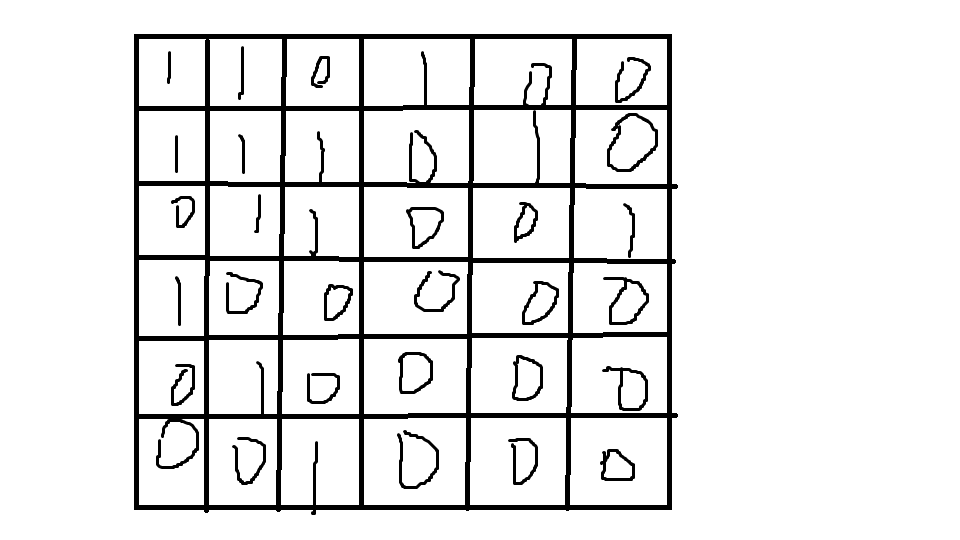
具体还是看CODE吧，然后就是常规的矩阵快速幂了

CODE

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=55,mod=30011;
int n,m;
struct Matrix
{
    int n,m;
    LL a[N<<1][N<<1];
    inline void Dt_init(void)
    {
        register int i; memset(a,0,sizeof(a)); n>>=1;
        for (i=1;i<=n;++i)
        a[i][i+n]=a[i+n][i]=1;
        for (i=1;i<=n;++i)
        {
            if (i^1) a[i][i-1]=1;
            if (i^n) a[i][i+1]=1;
            a[i][i]=1;
        } n<<=1;
    }
    inline void cri_init(void)
    {
        register int i; memset(a,0,sizeof(a)); 
        for (i=1;i<=n;++i)
        a[i][i]=1;
    }
};
inline Matrix mul(Matrix A,Matrix B)
{
    Matrix C; C.n=A.n; C.m=B.m; memset(C.a,0,sizeof(C.a));
    for (register int i=1;i<=C.n;++i)
    for (register int j=1;j<=C.m;++j)
    for (register int k=1;k<=A.m;++k)
    C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%mod;
    return C;
}
inline Matrix quick_pow(Matrix A,int p)
{
    Matrix T; T.n=T.m=A.n; T.cri_init();
    while (p)
    {
        if (p&1) T=mul(T,A);
        A=mul(A,A); p>>=1;
    }
    return T;
}
int main()
{
    scanf("%d%d",&n,&m);
    Matrix A; A.n=A.m=n<<1; A.Dt_init();
    A=quick_pow(A,m-2);
    printf("%lld",(A.a[n][1]+A.a[n-1][1])%mod);
    return 0;