文章目录
1. ECDSA算法简介
1.1 椭圆曲线
针对目前的应用,椭圆曲线可以暂时理解为描述了特定点的集合的公式
y ^ 2=x^3+ax+b
下面给出一些a和b参数变化时候的曲线。

图1 b=1,a取值范围2到-3
我们可以基于椭圆曲线定义一个群,这个群满足以下特点:
a)群里的元素都在椭圆曲线上
b)椭圆上的单位元指的是无限远点
c)椭圆上的点p的逆元与P关于x轴对称
d)加法满足以下规则:对于在同一条直线上的非零点P、Q、R有P+Q+R=0;
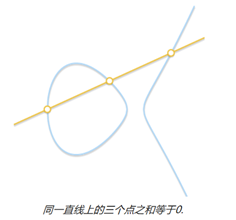
椭圆曲线是连续的,并不适合用于加密;所以,我们必须把椭圆曲线变成离散的点,我们要把椭圆曲线定义在有限域上。
我们给出一个有限域Fp,具有以下特性:
a)Fp中有p(p为质数)个元素0,1,2,…, p-2,p-1
b)Fp的加法是a+b≡c(mod p)
c)Fp的乘法是a×b≡c(mod p)
d)Fp的除法是a÷b≡c(mod p),即 a×b^(-1)≡c (mod p)
e)Fp的单位元是1,零元是 0
f)Fp域内运算满足交换律、结合律、分配律
椭圆曲线Ep(a,b),p为质数,x,y∈[0,p-1]
y2=x3+ax+b (mod p)
Fp上的椭圆曲线同样有加法:
a)无穷远点 O∞是零元,有O∞+ O∞= O∞,O∞+P=P
b)P(x,y)的负元是 (x,-y mod p)= (x,p-y) ,有P+(-P)= O∞
c)P(x1,y1),Q(x2,y2)的和R(x3,y3) 有如下关系:
x3≡k^2-x1-x2(mod p)
y3≡k(x1-x3)-y1(mod p)
若P=Q 则 k=(3 x2^2+a)/2y1mod p
若P≠Q,则k=(y2-y1)/(x2-x1) mod p
例椭圆曲线已知E23(1,1)上一点P(3,10)求2P
k=(33 ^ 2+1)/(210) mod 23=75^(-1) mod23
55 ^ (-1)=1mod23得到5^(-1)=14
则K=714mod23 = 6
则2P = (6^2-3-3mod23,6(3-7)-10mod23)=(7,12)
更一般的计算nP=P+P+P……+P
例如n=151,它的二进制表示形式为10010111 。二进制表示形式可以转换为一系列2的幂之和
151=12 ^ 7+02 ^ 6+02 ^ 5+12 ^ 4+02 ^ 3+12 ^ 2+12 ^ 1+12^0
则151*P=2 ^ 7 P+2 ^ 4 P+2 ^ 2 P+2 ^ 1 P+2^0 P
则先求P加倍得到2P,将2P与P相加,得到2 ^ 1 P+2 ^ 0 P,将2P加倍,得到2 ^ 2 P,与前一结果相加得到2 ^ 2 P+2 ^ 1 P+2^0 P,依次类推,计算151P需7次“加倍”运算和4次“相加”运算
1.2 椭圆曲线密码(ECC)
1985 年,V.Miller 和 N.Koblitz 各自独立地提出椭圆曲线公钥密码。椭圆
曲线密码是用有限域上的椭圆曲线构成的群来类比有限域的乘法群,从而得到类
似于使用有限域乘法群的公钥密码体制。椭圆曲线密码体制的安全性是基于椭圆
曲线上离散对数问题求解的困难性,这个问题目前还没有找到能够有效解决的亚
指数时间算法。
椭圆曲线密码具有的一些优点是其他公钥密码体制所无法比拟的。例如,在相同的安全要求下,椭圆曲线密码所需要的参数和密钥尺寸较短,参数选择余地较大。由于椭圆曲线密码所具备的优点,若干年来,一直受到密码学研究者们的关注,在理论和技术上都获得了大量的研究成果。并且,目前许多国际标准化组织,都已经在各种标准化文件中使用了椭圆曲线密码体制,并向全球颁布。
1.3 数字签名(DSA)
数字签名是公钥密码的重要应用,是解决信息安全问题的一项重要技术手
段。它可以以实现身份认证、保护数据完整性、防止数据篡改以及实现数据的不
可否认性等多种信息安全中的重要需求。因此,数字签名技术是信息安全核心技
术之一。目前,许多国家和地区都相继通过法律来赋予了数字签名的法律效益,
使数字签名可以作为一种重要的数字证据。我国在2004年8月也通过了《中华人民共和国电子签名法》,这部法律颁布之后,在我国数字签名也将与传统的手写签名一样具有同等法律效力。
1.4 椭圆曲线数字签名(ECDSA)
椭圆曲线密码自出现以来,便受到了研究者们的关注与重视。由于它拥有其
他公钥密码体制无法比拟的优势,目前在各个领域中逐渐产生了取代了经典的
RSA 公钥密码体制的趋势。随着椭圆曲线密码体制的逐步普及,椭圆曲线数字签名也成为了研究者们的关注的重点之一。椭圆曲线数字签名是椭圆曲线密码体制的重要应用之一,它将椭圆曲线密码的优势应用到了数字签名当中。
2. ECDSA算法描述
ECDSA算法包括椭圆曲线数字签名的生成和验证算法,下文将分别介绍。
2.1 椭圆曲线数字签名生成算法
椭圆曲线数字签名生成算法主要分3步。
首先输入ECDSA域参数D=(q,a,b,G,n,h),
a)域的大小q;
b)Fq上椭圆曲线E的等式定义的Fq上的两个元素a和b
c)定义E(Fq)中素数阶有限点G=(xG,yG)的Fq上的两个域元素xG和yG;
d)点G的阶数n(如果椭圆曲线上一点P,存在最小的正整数n使得数乘nP=O∞ ,则将n称为P的阶);
e)伴随因子h=#E(Fq)/n(椭圆曲线上所有点的个数m与n相除的商的整数部分)。
一般实际应用时域参数采用SECG或NIST标准组织推荐的参数。
然后生成ECDSA密钥对(d,Q),d为私钥,Q为公钥
最后生成ECDSA签名(r,s)。
2.2 椭圆曲线数字签名验证算法
ECDSA签名验证算法的数学公式为:
P = S^-1 X z X G +S ^-1 X R X Qa
(其中Z为哈希计算值)
若计算结果P的x坐标与R相等,则签名有效
3. ECDSA算法步骤
3.1 椭圆曲线数字签名生成算法
a) 选取ECDSA域参数D=(q,a,b,G,n,h)
b) 生成ECDSA密钥对生成 (d,Q),Q = d * G
c) 取一个范围在[1,n-1]的随机数k ,32字节
d) 计算点P = kG
e) 计算r=Px mod n
f) 若r= =0 跳转至c步
g) 计算s=k ^ -1(z+r*d)mod n (d是私钥 k^-1是k对n的逆元 ,z是哈希计算值)
h) 如果s==0,跳转至c步
二元组r ,s就是签名值
3.2 椭圆曲线数字签名验证算法
ECDSA签名验证算法的数学公式为:
P = S^-1 X z X G +S ^-1 X R X Qa
若P的x坐标与R相等,验证成功,否则失败。
3.3 运算模块
从以上算法过程介绍可以看出ECDSA算法主要包含以下几个运算模块
模乘模块、模加模块、模逆模块、求模模块、Hash模块
ECDSA算法的难点在于设计高效的各模块算法,像知名的蒙哥马利乘法,Stein求逆等都是上述模块的一些实现方式。
