并查集总结（不看后悔系列）

写在前面：并查集能在一张无向图中维护节点之间的连通性，这是他的基本用途之一。实际上并查集擅长动态维护许多具有传递性的关系。

文章目录

定义：
普通并查集

理解
实现
[Codeforces Round #595 (Div. 3)](https://codeforces.com/contest/1249)B2

边带权并查集
扩展域并查集

定义：

在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

$Find:$ 确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
$Union：$ 将两个子集合并成同一个集合。

由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构（union-find data structure）或合并-查找集合（merge-find set）。
注:并查集并不支持集合的分离和删除

普通并查集

理解

我们经常会遇到处理两个集合关系的题目，比如某些集合合并的问题，或者判断两个元素是否同在一个集合里。而并查集其实就是相当于这每个集合中找一个代表元(老大)，来表示这个集合，如下图(网络图片）
在这里插入图片描述
我们在每个集合里找一个"老大”做代表，然后查询的A,B是否在一个集合时，A说我老大是C，B说我老大也是C，那么A和B就知道他们在同一个集合了；如果A的老大是C，B的老大是D，那么A、B就不在同一个集合了，要使得A、B所处的集合合并，要么C成为D的老大了，要么D成为C的老大了。这就是基本的思想。

实现

我们用一个数组 $fa[i]$ 来表示 $i$ 的老大是谁，一开始每个人都是自己的老大。

初始化

int fa[N];
void init(){
    for(int i = 1;i <= n;++ i) fa[i] = i;
}

$Find$

然后，我们查找A、B是否在同一个集合时，是一直找A的老大的老大的… ,B也是同理，知道满足某个条件，就停下来，找到集合的老大了！比如按上述初始化方式，当 $fa[x]=x$ 时，说明 $x$ 就是集合的老大。比如下图：(图片来自网络
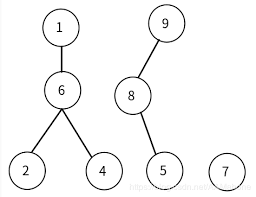
在这里插入图片描述
我们查询 $2,5$ 是否在一个集合中,
$2:$ $fa[2]=6,fa[6]=1,fa[1]=1$
$5:$ $fa[5]=8,fa[8]=9,fa[9]=9$

最后发现他们的老大不同唉，说明不在一个集合。而这个过程，是不断递归的找老大的。

int Find(int x){
    if(fa[x] == x) return x;
    else return Find(fa[x]);
}

可是这样最坏的情况下使树链，每次查询都是 $O(N)$ 的，我们介绍两种优化方法，路径压缩和按秩合并

路径压缩
如果是树链状，每次询问A的老大是谁，他就会问 $fa[A]$ 老大是谁， $fa[A]$ 就会问 $fa[fa[A]]$ 老大是谁，这样下去，一直到有个人 $root$ 说老大是我！这样传递的速度太慢了，而如果这条路径的人不傻，那么在老大 $root$ 向A传老大是我的的路途中，这条路径的人都知道这个集合真正的老大是谁了，而不用在问自己的老大集合中的老大是谁了，也就是对于路径中每个 $x$ ， $fa[x]=root$ .
这样就改变了树的形状。如下图(图片来自网络

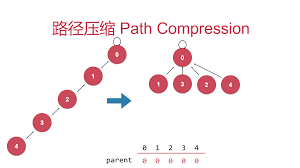
int Find(int x){
    if(fa[x] == x) return x;
    else return fa[x] = Find(fa[x]);
}

$Union$
上面我们提到了，当两个集合进行合并时，其实就是让两个集合中一个老大认另一个老大做老大(有点拗口
(图片来自网络）
在这里插入图片描述
合并A、B的集合，肯定得找来他们各自的老大来说事啊！

void Union(int x,int y){
    int q = Find(x);
    int p = Find(y);
    if(q != p) fa[x] = y;
}

按秩合并
你可以理解为是按各自集合树的深度合并，在这个算法中，术语“秩”替代了“深度”，秩将不会与高度相同。单元素的树的秩定义为 $0$ ，当两棵秩同为 $r$ 的树联合时，它们的秩 $r+1$ 。当前有时候我们也常常按照集合的大小进行合并，顺便还维护每个集合中元素的数目。
以下两种都可以用，但是一般题目只用路径压缩就够了。

int Rank[N];//秩初始化为0
void Union(int x,int y){
    int q = Find(x);
    int p = Find(y);
    if(q != p){
        if(Rank[q] > Rank[p]) fa[p] = q;
        else if(Rank[q] < Ran[p]) fa[q] = p;
        else {
            fa[q] = p;
            Ran[p] ++;
        }
    }
}

int Size[N];//初始化为1
void Union(int x,int y){
    int q = Find(x);
    int p = Find(y);
    if(q != p){
        if(Size[q] > Size[p]) fa[p] =q,Size[q] += Size[p];
        else fa[q] = p,Size[p] += Size[q];
    }
}

Atcoder D - Friend Suggestions(并查集）
题意：
有 $n$ 个人， $m$ 对双向的朋友关系，还有 $k$ 对破裂的关系。
现在让你找 $i$ 的候选朋友，候选朋友是 $i$ 的朋友的朋友（间接朋友关系），并且还不是破裂关系。问每个 $i$ 有多少个候选朋友。
思路：
朋友的传递关系显然可以用并查集进行合并，同时我们用 $Size[N]$ 数组维护每个集合的大小。
我们进行 $dfs$ 找每个人的可能的朋友关系并进行集合的合并。每个集合中的人都互为朋友。
那么对于任意点 $i$ 来说，它所在并查集的连通块中都是它可以通过它的朋友可以到达的，但是这其中也有和它直接是朋友的和有破解关系的朋友。我们用 $i$ 所在集合的大小 $-$ 和它直接是朋友的 $-$ 有破裂关系的 $-$ 他自己 $= ans$ 。

struct Edge{
    int next;
    int to;
}edge[N];
int head[N],tot;
inline void add(int from,int to){
    edge[++tot].next = head[from];
    edge[tot].to = to;
    head[from] = tot;
}
int cnt[N];
int pre[N];
int Find(int x) {return pre[x]==0?x:pre[x] = Find(pre[x]);}
int Size[N];
int ans[N];
void join(int x,int y){
    int q = Find(x),p = Find(y);
    if(q != p){
        if(Size[q] > Size[p]) pre[p] = q,Size[q] += Size[p];
        else pre[q] = p,Size[p] += Size[q];
    }
}
bool vis[N];
void dfs(int x){
    vis[x] = 1;
    for(int i = head[x];i;i = edge[i].next){
        int  y = edge[i].to;
        if(!vis[y]){
            join(x,y);
            dfs(y);
        }
    }
}
int main(){
    int n = read(),m = read(),k = read();
    fill(Size+1,Size + n +1,1);
    rep(i,1,m){
        int u = read(),v = read();
        cnt[u] ++;//储存直接边
        cnt[v] ++;
        add(u,v);
        add(v,u);
    }
    for(int i = 1;i <= n;++i) dfs(i);//进行集合关系的划分
    rep(i,1,k){
        int u = read(),v = read();
        if(Find(u) == Find(v)) cnt[u] ++,cnt[v] ++;//如果这两个破裂关系在一个连通块，那么就减去
    }
    rep(i,1,n) cout << Size[Find(i)] - cnt[i] - 1<<' ';
}

Codeforces Round #595 (Div. 3)B2

题意：

给你一个数列，其中每个位置 $i$ 出值为 $p[i]$ 代表 $i-> p[i]$ 就是从 $i$ 到 $p[i]$ 的意思。问你每个位置至少需要多少步才能到自身。

思路：

想了一大会儿。。。。每个数字能到自身的话说明会有一个环，那么环上的点到他们的长度都是这个环的长度。所以我们只要有用并查集合并环是上的点，同时 $Size$ 记录这个环的大小就行了。

int Size[N];
int fa[N];
int Find(int x) {return fa[x] == -1?x:fa[x] = Find(fa[x]);}
void Union(int x,int y){
  int q = Find(x),p = Find(y);
  if(Size[q] > Size[p]) swap(q,p);
  if(q!=p) {fa[q] = p;Size[p] += Size[q];}
}
int main(){
  int  t = read();
  while(t--){
    int n = read();
    fill(Size+1,Size+n+1,1);
    memset(fa,-1,sizeof fa);
    rep(i,1,n){
      int a = read();
      Union(i,a);
    }
    rep(i,1,n){
      cout << Size[Find(i)]<<' ';
    }
    puts("");
  }
}

AcWing 237. 程序自动分析
题意：
在这里插入图片描述
思路：
只有等和不等两种关系，问你是否会产生矛盾，在线做法还是比较麻烦的，离线做法就好想了，我们先把相等关系的用并查集合并在一起，然后在检查不等关系是否在一个集合中。
因为数据范围比较大，难以放在数组中，所以我们先离散化一下，在处理。

int fa[N];
int x[N],y[N],op[N];
int b[N];
int Find(int x){return fa[x] == 0?x:fa[x] = Find(fa[x]);}
int main(){
    int t = read();
    while(t--){
        memset(fa,0,sizeof fa);
        int n = read();
        int tot(0);
        rep(i,1,n){
            x[i] = read(),y[i] = read(),op[i] = read();
            b[++tot] = x[i];
            b[++tot] = y[i];
        }
        sort(b+1,b+tot+1);//离散化
        int m = unique(b+1,b+tot+1) - b - 1;
        rep(i,1,n){
            x[i] = lower_bound(b+1,b+m+1,x[i]) - b;
            y[i] = lower_bound(b+1,b+m+1,y[i]) - b;
        }
        rep(i,1,n){
            if(op[i] == 1){
                int q = Find(x[i]);
                int p = Find(y[i]);
                if(q!=p) fa[q] = p;
            }
        }   
        bool r = 1;
        rep(i,1,n){
            if(op[i] == 0){
                int q = Find(x[i]);
                int p = Find(y[i]);
                if(q == p) {r = 0;break;}
            }
        }    
        if(r) puts("YES");
        else puts("NO");
    }
}

边带权并查集

并查集实际上是由若干棵树构成的深林，我们可以在树中的每条边上记录一个权值，即维护一个数组 $d$ ，用 $d[x]$ 保存节点 $x$ 到父节点 $fa[x]$ 之间的边权。在每次路径压缩后，每个访问过的节点都会直接指向树根，如果我们同时更新这些节点的 $d$ 值，就可以利用路径压缩过程来统计每个节点到树根之间的路径上的一些信息(以根为中介)。
考虑到权值就会有以下问题：

每个节点都记录的是与根节点之间的权值，那么在Find的路径压缩过程中，权值也应该做相应的更新，因为在路径压缩之前，每个节点都是与其父节点链接着，那个Value自然也是与其父节点之间的权值
在两个并查集做合并的时候，权值也要做相应的更新，因为两个并查集的根节点不同

路径压缩

int Find(int x){
    if(fa[x] == x) return x;
    int y = Find(fa[x]);//递归找集合代表
    d[x] += d[fa[x]];//维护d数组 —— 对边权求和
    return fa[x] = y;//路径压缩
}

因为在路径压缩后父节点直接变为根节点，此时父节点的权值已经是父节点到根节点的权值了，将当前节点的权值加上原本父节点的权值，就得到当前节点到根节点的权值

AcWing 238. 银河英雄传说
在这里插入图片描述
思路：
M 命令说 $i$ 号战舰所在列保持原有顺序放在 $j$ 号战舰所在列尾部。
C 命令是查询是否在同一个序列，是的话输出之间有多少艘飞船。
很显然，每个序列就是一条链，我们要处理涉及集合的查询合并问题，不免想到并查集，可是这里还有关于值的查询，因为都是链，我们用数组 $d[i]$ 表示 $i$ 之前有多少艘飞船，然后关于值的查询 $<i,j>$ 就等于 $|d[i]-d[j]|-1$ 。

int fa[N];
int d[N];
int Size[N];
int Find(int x){
    if(fa[x] == 0) return x;
    int y = Find(fa[x]);
    d[x] += d[fa[x]];//更新x点到新的根的距离
    return fa[x] = y;
}
int main(){
    int t = read();
    fill(Size+1,Size+t+1,1);
    memset(fa,0,sizeof fa);
    while(t--){
        char c = gc();int u = read(),v = read();
        if(c=='M'){
            int x = Find(u),y = Find(v);
            if(x!=y){
                d[x] = Size[y];//x所在列到y所在列的尾部，所以d[x]=Size[y]
                Size[y] += Size[x];//y所在列维护多了长度为Size[x]的列
                fa[x] = y;
            }
        }
        else {
            int x = Find(u),y = Find(v);
            if(x!=y) puts("-1");
            else{
                cout<<abs(d[u]-d[v])-1<<endl;
            }
        }
    }
}

ACwing 239. 奇偶游戏
在这里插入图片描述
思路：
这个思路真没想到啊(虽然以前做过一次
这个题目，给你 $m$ 信息，每个区间内可能有偶数个1或者奇数个1。然后让你输出最多到哪个位置可以保证前面说的话全是对了。
这个题目有一个~~很典型的~~ 好的技巧，就是将原问题的区间相关问题，转化为了区间端点的问题。
首先我们先分析数据范围，发现也是数的范围很大，但是查询相比却很少，于是乎我们先保存离线处理，离散化一下。
如果说 $[l,r]$ 区间内有偶数个1，那么 $sum[r]-sum[l-1]$ 为偶数，根据奇偶性质， $sum[r]和sum[l-1]$ 的奇偶性应该相同；有奇数个1，那么 $sum[r]$ 和 $sum[l-1]$ 奇偶性应该不同。
我们用 $d[i]=0$ 表示第 $i$ 和根的奇偶性相同，1表示和根的奇偶性相同。
对于给的每个区间的信息，我们看 $l-1$ 和 $r$ 是否在同一个集合内，若在，则看 $d[l-1]$ 和 $d[r]$ 的奇偶性关系是否和给的信息符合；若不在，则合并两个并查集，注意我们要在两个并查集的集合代表之间连一条边，这个边的权值应该为什么呢？
对于给定信息 $[l,r,ans]$ 我们不妨设偶数时 $ans=0$ (因为前面说两个数奇偶性相同时为0），奇数时 $ans=1$ 。那么 $d[l-1]\oplus d[r]\oplus d[p]=ans$ 。所以 $d[p]=d[l-1]\oplus d[r]\oplus ans$
，和上题对比一下，差不多的套路。

int fa[N];
int x[N],y[N];char op[N];
int a[N],tot;
int d[N];
int Find(int x){
    if(fa[x] == 0) return x;
    int y  = Find(fa[x]);
    d[x] ^= d[fa[x]];
    return  fa[x] = y;
}
int main(){
    int n = read();
    int m = read();
    rep(i,1,m){
        int u = read(),v = read();
        char s[5];
        scanf("%s",s);
        x[i] = u-1;y[i] = v;
        op[i] = s[0];
        a[++tot] = u;a[++tot] = v;
    }
    sort(a+1,a+tot+1);//离散化
    int S = unique(a+1,a+tot+1)-a-1;
    rep(i,1,m){
        x[i] = lower_bound(a+1,a+S+1,x[i]) - a;
        y[i] = lower_bound(a+1,a+S+1,y[i]) - a;
    }
    bool r = 1;
    rep(i,1,m){
        int q = Find(x[i]),p = Find(y[i]);
        if(op[i] == 'e'){
            if(q == p){
                if(d[x]^[y]!=0) {cout<<i-1;return 0;}
            }
            else{
                d[q] = d[x]^[dy]^0;
                fa[q] = p;
            }
        }
        else{
            if(q == p){
                if(d[x]^d[y]!=1) {cout<<i-1;return 0;}
            }
            else{
                d[q] = d[x]^d[y]^1;
                fa[q] = p;
            }
        }
    }
    cout<<m;
}

扩展域并查集

按照我的理解，扩展域的并查集是维护一种逻辑上的关系，对于 $x$ ,并不知道它的具体值，但我们拆点拆点来表示 $x$ 的情况，然后根据题意用并查集维护 $x,y$ 之间的关系。

ACwing 239. 奇偶游戏
上面用带边权的并查集解决的，接下来使用扩展域的并查集解决。
由上面可知，我们区间问题，我们借助前缀和+奇偶特性转变为了处理两个端点的问题。然后对于这题，我们离散化后拆点建立两个域，奇数域和偶数域，S为离散化后的点数，不妨零 $[1,S]$ 为偶数域， $[S+1,S+S]$ 为奇数域，对于给出的信息 $[l,r,ans]$ ，若 $ans$ 为偶数，那么说明 $l-1,r$ 同奇偶，我么合并 $l-1,r$ 和 $l-1+S,r+S$ ，如果为奇数，说明两个数奇偶性不同，我们合并 $l-1,r+S$ 和 $l-1+S,r$ 。
当然，每次给出的信息都先检查一下给的的奇偶性关系是否和域中关系一致。

int x[N],y[N];char op[N];
int a[N],tot;
int fa[N];
int Find(int x){return fa[x] == 0?x:fa[x] = Find(fa[x]);}
int main(){
    int n = read();
    int m = read();
    rep(i,1,m){
        x[i] = read()-1;
        y[i] = read();
        op[i] = gc();
        a[++tot] = x[i];
        a[++tot] = y[i];
    } 
    sort(a+1,a+tot+1);//离散化
    int S = unique(a+1,a+tot+1) - a - 1;
    rep(i,1,m){
        x[i] = lower_bound(a+1,a+S+1,x[i]) - a;
        y[i] = lower_bound(a+1,a+S+1,y[i]) - a;
    }
    rep(i,1,m){
        int q = Find(x[i]),p = Find(y[i]);//偶数域
        int w = Find(x[i]+S),e = Find(y[i]+S);//奇数域
        if(op[i] == 'e'){
            if(w == p) {cout<<i-1;return 0;}
            else if(q != p){fa[q] = p;fa[w] = e;}
        }
        else {
            if(q == p) {cout<<i-1;return 0;}
            else if(q!=e){fa[q] = e;fa[p] = w;}
        }
    }
    cout<<m;

}

AcWing 240. 食物链
在这里插入图片描述
思路：
我么维护三个域，同类域 $(x,y)$ ，捕食域 $(x+n,y+n)$ ，天敌域 $(x+2*n,y+2*n)$ 。

对于
$x,y$ 是同类的信息，我们检查是否有矛盾，即看是否有其他关系， $x$ 吃 $y$ 或者 $y$ 吃 $x$ ，那么对于 $x$ 吃y，我们只需看 $x$ 和 $y+2*n$ （y的天敌域）是否是同一类， $y$ 吃 $x$ 同理。如果没矛盾，那么我们将合并 $(x,y),(x+n,y+n),(x+2*n,y+2*n)$ 。
对于
$x$ 吃 $y$ 的信息，我们看有没有矛盾，即是否有其他关系， $y$ 吃 $x$ 或者 $y$ 和 $x$ 同类。 $y吃x$ 和上面那类一样一样处理，那检查 $x、y$ 是否同类，只需要检查他们是否在一个集合。如果没矛盾，就合并 $(x,y+2*n),(x+n,y),(x+2*n,y+n)$ 。

int fa[N];
int Rank[N];
int Find(int x){return fa[x] == 0?x:fa[x] = Find(fa[x]);}
void Union(int x,int y){
    int q = Find(x),p = Find(y);
    if(q != p){
        if(Rank[q] > Rank[p]) fa[p] = q;
        else if(Rank[q] < Rank[p]) fa[q] = p;
        else {
            fa[q] = p;
            Rank[p]++;
        }
    }
}
int op,n,k,x,y,q,p,a,b;
int main(){
    n = read(),k = read();
    int ans = 0 ;
    rep(i,1,k){
        op = read(),x = read(),y = read();
        if(x>n||y>n) {ans++;continue;}
        q = Find(x), p = Find(y);
        a = Find(x+2*n),b = Find(y+2*n);
        if(op == 1){
            if(q == b||p == a) ans++;
            else {
                Union(x,y);
                Union(x+n,y+n);
                Union(x+2*n,y+2*n);
            } 
        }
        else {
            if(x == y) {ans ++;continue;}
            if(p == a||p == q) ans ++;
            else {
                Union(x,y+2*n);
                Union(x+n,y);
                Union(x+2*n,y+n);
            }
        }
    }
    cout << ans;
}