文章目录
2.2母函数
-
组合数学用的最多的工具要算母函数,什么是母函数,
-
-
系数: 取 个组合的全体之和
-
令都=1
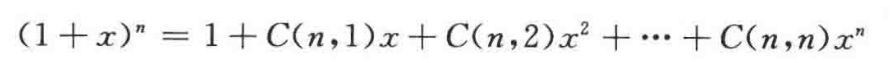
- 另一方面
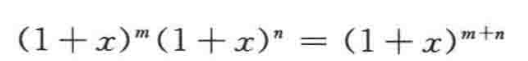

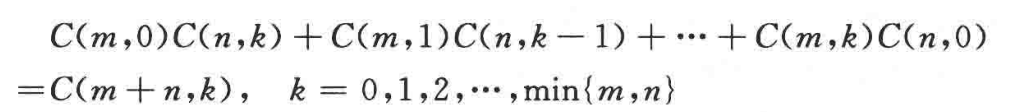
here
- 定义2-1
- 序列 , , ,…
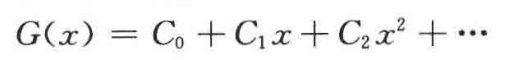
-
为序列的母函数
-
序列长度有限,也可无限
- 序列和对应的母函数是一一对应
- 序列 …为
2.8整数的拆分
- 母函数将问题转换为关于母函数的某种代数问题,
- 甚至变成关于母函数的某种形式的运算,
- 整数的拆分为例.
- 正整数 分解为若干个正整数的和,不考虑求和顺序
- n=2,2=1+1,
- n=3,1+2,1+1+1
- n=4,1+1+1+1,1+1+2,1+3,2+2
- 正整数 拆分成若干正整数的和,
- 拆分个数用
- 正整数拆分可理解为将
个无区别的球,
- 放人 个无区别盒子
- 每种方案就是一种拆分
- 1克、2克、3克、4克的砝码各一,
- 能称出多少重量,各有几种称法
- 可看成将 拆分成1,2,3,4之和且不允许重复的拆分数,
- 利用母函数计算
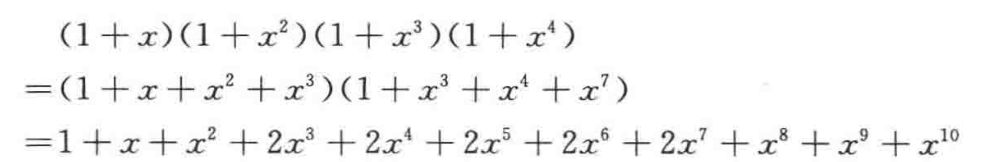
-
:称出3克的有2种方案,
- 1+2,3,
- 超10无法称出
here
2.14非线性递推关系举例
- 前面的线性常系数齐次递推关系,基本上得到全部解决
- 非齐次递推关系只有部分能解
- 非线性递推关系只能涉及较特殊的几个
- 几个典型的例子
2.14.1 Stirling数
- 个有区别球
- 两个有标志盒子
- 第一个放 个,则第二个为 个,
- 这样的方案数正好是 中 项的系数
- 有
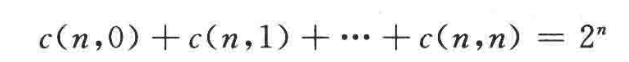
-
有区别球放进
有标志盒子,要求
个有标志的盒子的
球数为 - 方案数


- 也可看作将
个有标志的球全排列,
- 依次取 个放进第一盒,
- 余下 个放进第二个盒
- 但盒子中球无顺序
- 故得到不同的方案数为那么多
- 称

- 为 的多项式系数
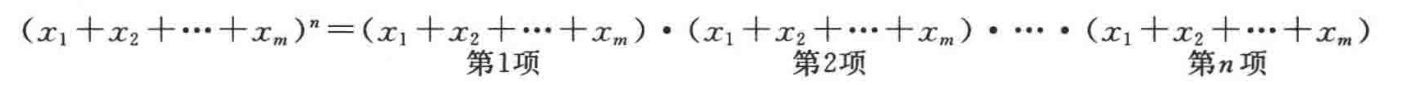
- 第 项对应第 个有区别的球,
- 取 对应于第 个盒子,
- 第 项取 对应将第 个球放进第 个盒
- 它的展开式为
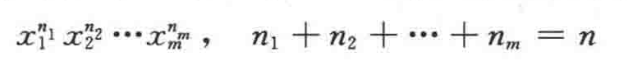
- 表示第一个盒子里有 个球,第二个里有 个球,…,
- 所以,
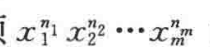
的系数为
- 定理2-5
- 展开式的项数等于
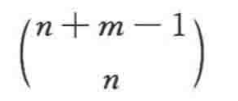
- 系数和等于啥

- 这里只论第2类司特林数,
- 第1类司特林数则只给出其定义和递推关系

-
定义2-3
-
个有区别的球放到 个相同盒子,要求无一空盒
-
方案数 ,称第2类司特林数
-
就是将 个数拆分成非空的 个部分的方案数
-
红、黄、蓝、白4颜色,两个无区别盒子
- 不许空盒,
- 如下7种

here
2.14.2 Catalan数
- 凸n边形通过不相交于
边形内部的对角线把
- n边形拆分成若干三角形,
- 不同拆分数用
- 五边形有5种

1.关于 Catalan数的递推关系
- 定理2-8
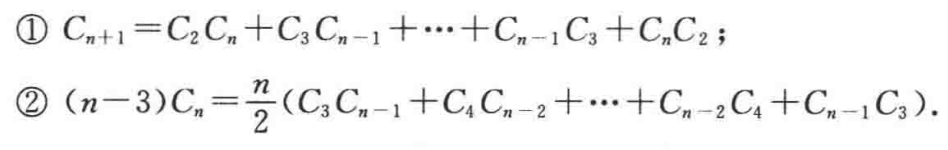
-
①的证明:
-
2-19的n+1边形,
-
以 作为三角形的一条边,三角形的另一个顶点为 , ,
-
三角形 将 边形分割成
- 边形,
- 边形
-
以 为一剖分三角形的剖分数应为
, -
所得的剖分各不相同

