机器学习算法通常需要大量的数值计算。这通常指通过迭代过程更新解得估计值来解决数学问题的算法，而不是通过解析过程推导出公式来提供正确解的方法。常见的操作包括优化和线性方程组的求解。
1、上溢和下溢
连续数学在数字计算机上的根本困难是，我们需要通过有限数量的位模式来表示无限多的实数。这意味着我们在计算机中表示实数时，几乎总会引入一些近似误差。在许多情况下，这仅仅是舍入误差。舍入误差会导致一些问题，特别是当许多操作复合时，即使是理论上可行的算法，如果在设计时没有考虑最小化舍入误差的累积，在实践中也可能会导致算法失效。
下溢：当接近零的数被四舍五入为零时发生下溢。许多函数在其参数为零而不是一个很小的正数时才会表现出质的不同
上溢：当大量级的数被近似为∞或-∞时发生上溢。进一步运算通常导致这些无限值变为非数字
必须对上溢和下溢进行数值稳定的一个例子是softmax函数。softmax函数经常用于测试与Multinoulli分布相关联的概率，定义为
解决办法是，计算softmax(z)， 
，softmax解析上的函数不会因为从输入向量减去或加上标量而改变。减去 
导致exp最大参数为0，这排除了上溢的可能性；同样，坟墓中至少有一个值为1的项，这就排除了因分母下溢而导致被零除的可能性。
另一个小问题是分子的下溢扔可以导致整体表达式被计算为零，这意味着在计算log(softmax(x))时会错误地得到-∞
2 、病态条件
条件数指函数相对于输入的微小变化而变化的快慢程度。
考虑函数 
具有特征值分解时，其条件数为 
。即最大特征值和最小特征值的模之比。当该数很大时，矩阵求逆对输入的误差特别敏感。病态条件会放大预先存在的误差，在实践中，该错误将与求逆过程本身的数值误差进一步复合。
2.1 病态系统
现在有线性系统： Ax = b，解方程：
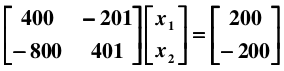
很容易得到解为： x1 = -100, x2 = -200. 如果在样本采集时存在一个微小的误差，比如，将 A 矩阵的系数 400 改变成 401：
则得到一个截然不同的解： x1 = 40000, x2 = 79800.
当解集 x 对 A 和 b 的系数高度敏感，那么这样的方程组就是病态的 (ill-conditioned).
2.2 条件数
在二次方程中，椭球面的形状受海森矩阵的条件数影响，长轴与短轴分别对应海森矩阵最小特征值和最大特征值的特征向量的方向，其轴长与特征值的平方根成反比。最大特征值与最小特征值相差越大，椭球面越扁，优化路径需要走的路径越弯，计算效率很低。
最大特征值越大，最大特征值的平方根的倒数就越小，短轴越短，最小特征值越小，最小特征值的平方根的倒数就越大，长轴就越长；
短轴越短，长轴越长，椭球面越扁；
3、基于梯度的优化方法
把要最小化或最大化的函数称为目标函数或准则
当我们对其进行最小化时，也把它称为代价函数、损失函数或误差函数
导数为零的点称为临界点或驻点，当导数为零时无法提供往哪个方向移动的信息。
局部极小点：其值低于相邻点
局部极大点L其值高于相邻点
鞍点：既不是最小点也不是最大点
在多维情况下，“最小化”输出的必须是一维的标量
在多维情况下，临界点是梯度中所有元素都为零的点。
梯度下降：连续空间的优化问题
爬山算法：递增带有离散参数的目标函数
二阶导数告诉我们，一阶导数将如何随着输入的变化而改变，它表示只基于梯度信息的梯度下降步骤是否会产生如我们预期的那样大的改善。
二阶导数是对曲率的衡量，零二阶导数没有曲率，是一条完全平坦的线，仅用梯度就可以预测它的值。
如果曲率是负的，函数曲线向下凹陷（向上凸出），因此代价函数将下降的比ε多。
如果曲率是正的，函数曲线向上凹陷（向下凸出），因此代价函数下降得比ε少。
Jacobian矩阵：
Hessian矩阵：
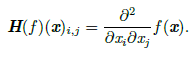
Hessian矩阵等于梯度的Jacobian矩阵
因为Hessian矩阵是实对称的，我们可以将其分解为一组实特征值和一组特征向量的正交基。在特定方向d上的二阶导数可以写成 
。当d时H的一个特征向量时，这个方向的二阶导数就是对应的特征值。对于其他方向d，方向二阶导数是所有特征值的加权平均，权重在0和1之间，且与d夹角越小的特征向量的权重越大。最大特征值确定最大二阶导数，最小特征值确定最小二阶导数。
点x(0) 处作函数f(x) 的近似二阶泰勒级数：
学习率ε，新的点：x(0)-ϵg，代入
其中有3 项：函数的原始值、函数斜率导致的预期改善、函数曲率导致的校正。当最后一项太大时，梯度下降实际上是可能向上移动的。当g⊤Hg 为零或负时，近似的泰勒级数表明增加ϵ 将永远使f 下降。
当g⊤Hg 为正时，通过计算可得，使近似泰勒级数下降最多的最优步长为：
二阶导数测试
在多维情况下，我们需要检测函数的所有二阶导数。
当Hessian 是正定的（所有特征值都是正的），则该临界点是局部极小点。
当Hessian 是负定的（所有特征值都是负的），这个点就是局部极大点。
如果Hessian 的特征值中至少一个是正的且至少一个是负的，那么x 是f 某个横截面的局部极大点，却是另一个横截面的局部极小点。
当所有非零特征值是同号的且至少有一个特征值是0 时，这个检测就是不确定的。这是因为单变量的二阶导数测试在零特征值对应的横截面上是不确定的。
多维情况下，单个点处每个方向上的二阶导数是不同。Hessian 的条件数衡量这些二阶导数的变化范围。当Hessian 的条件数很差时，梯度下降法也会表现得很差。这是因为一个方向上的导数增加得很快，而在另一个方向上增加得很慢。梯度下降不知道导数的这种变化，所以它不知道应该优先探索导数长期为负的方向。病态条件也导致很难选择合适的步长。步长必须足够小，以免冲过最小而向具有较强正曲率的方向上升。这通常意味着步长太小，以致于在其他较小曲率的方向上进展不明显。
当附近的临界点是最小点（Hessian 的所有特征值都是正的）时牛顿法才适用，而梯度下降不会被吸引到鞍点(除非梯度指向鞍点)
仅使用梯度信息的优化算法被称为一阶优化算法如梯度下降。使用Hessian 矩阵的优化算法被称为二阶最优化算法，如牛顿法。
凸优化算法只对凸函数适用，即Hessian 处处半正定的函数。因为这些函数没有鞍点而且其所有局部极小点必然是全局最小点，所以表现很好
4、约束优化
在x的某些集合S中找f(x)的最大值或最小值，这称为约束优化。在约束优化术语中，集合S内的点x称为可行点。
我们常常希望找到某种意义上小的解，针对这种情况下的常见方法是加强一个范数约束，如
KKT方法：S=
其中涉及g(i) 的等式称为等式约束，涉及h(j) 的不等式称为不等式约束
KKT 乘子：λi和αj
则 
和
有相同的最优目标函数值和最优点集x
KKT条件性质：
