图解 KMP算法

前言：点开这篇文章相信你可能已经对KMP算法有了一些了解，当然不了解也没有什么，我们今天就来细说一下什么是KMP算法，让你真正意义上的了解这个算法的原理与应用；

一、什么是KMP算法

• KMP 算法 全称为（Knuth-Morris-Pratt），就是一种改进的字符串匹配算法，最先由由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，它的出现无疑给字符串匹配带来了春天。
• 其实KMP算法的实质就是在匹配过程中，如遇到失配的环节，不会马上又从模式串的头开始匹配，而是会从模式串与当前匹配的字符串的子串的最大公共部分开始匹配，也就是我们要利用前面已经匹配的信息，从而丢弃掉一些不必要的过程，达到最小匹配时间。一点点言语是道不清的，还是请看下面的讲解。
• 一切算法的诞生都是为了满足我们的需求，KMP也不例外，例如下面这个需求就是KMP算法最经典的一个应用场景：
  当前我有一个字符串 str ，和另一个字符串pattern（暂且叫它模式串吧）
  我要问的是pattern 在str中是否存在，又或者pattern在str中出现了多少次；

二、暴力匹配

面对上面提出来了需求无疑大多数没有接触过KMP算法的小伙伴也就会首先想到这种算法（BF）暴力匹配。何为暴力匹配无非思路就是这样，定义一个
i=0，它指向的是str中的第i个字符，然后将 i 从 0 遍历到str.length - pattern.length. 在每次循环的过程当中又定义一个变量 j 它又表示指向的是pattern中的第 j 个元素，j 的取值呢就是 0 到 pattern.length，如果在此层循环中对于每个 j 表达式 str[i+j] == pattern[j] 都成立那么即为匹配成功，直到整个外层循环全部遍历完，都没有匹配成功的话，那么即判定pattern在str中不存在。
先看代码，这应该是大多数人首先想到的方法：

bool BF(string str,string pattern){
    int i=0,j=0;
    while(i < str.length() && j < pattern.length()){
        if(str[i] == pattern[j]){
            i++;
            j++;
        }else{
            i = i-j+1;
            j=0;
        }
    }
    return j == pattern.length();
}

这种算法的执行过程可以用下图来进行表示：

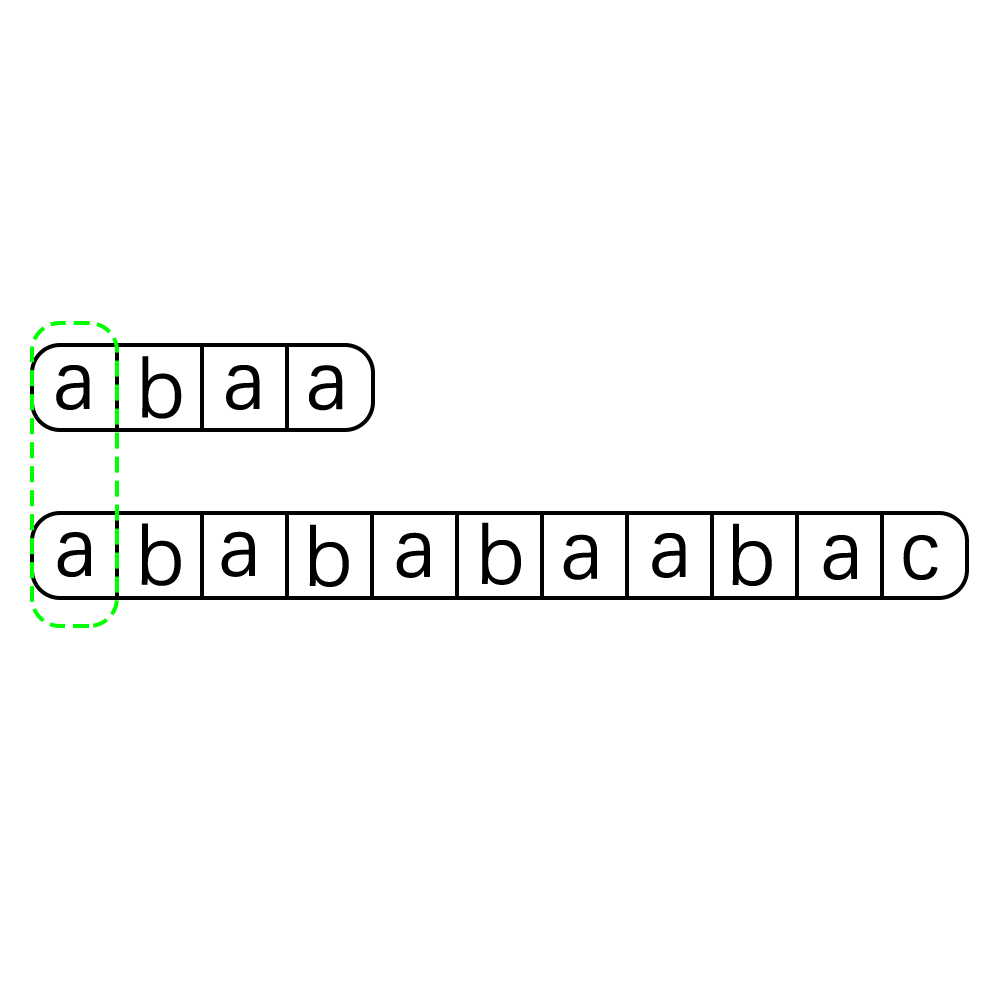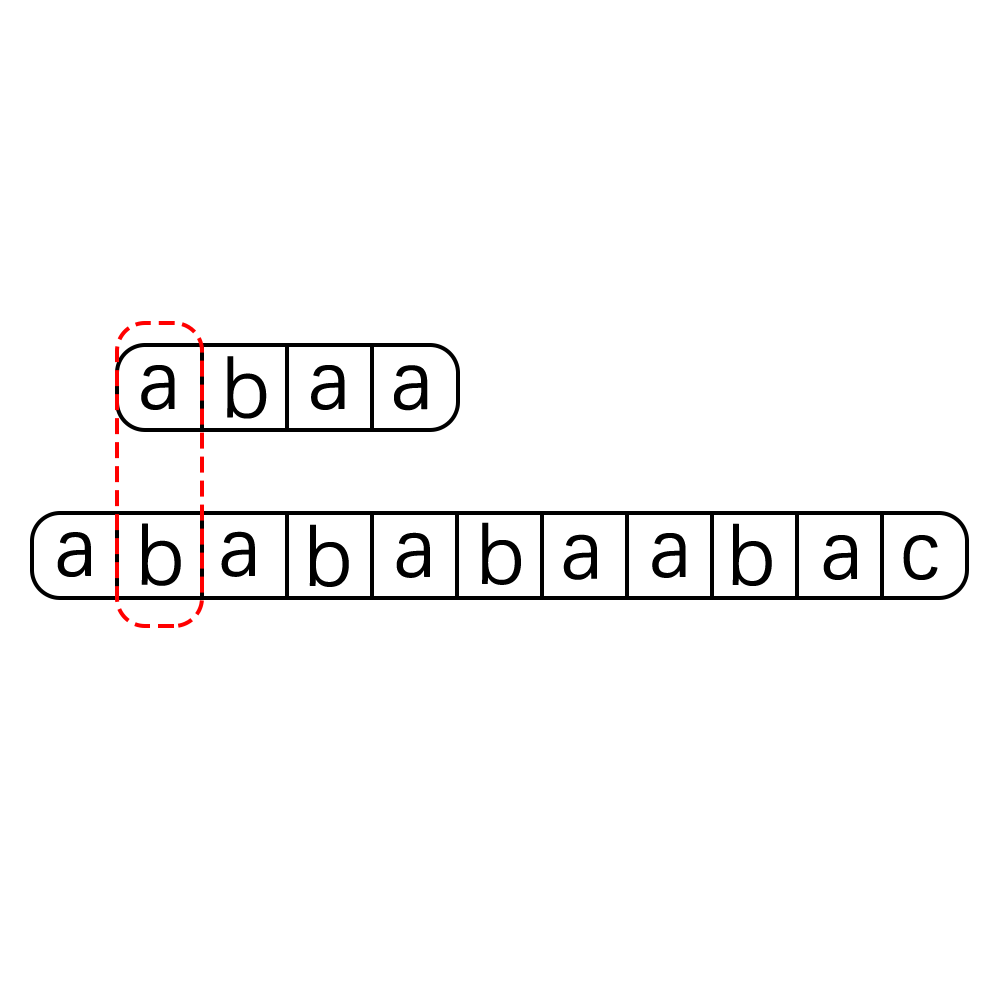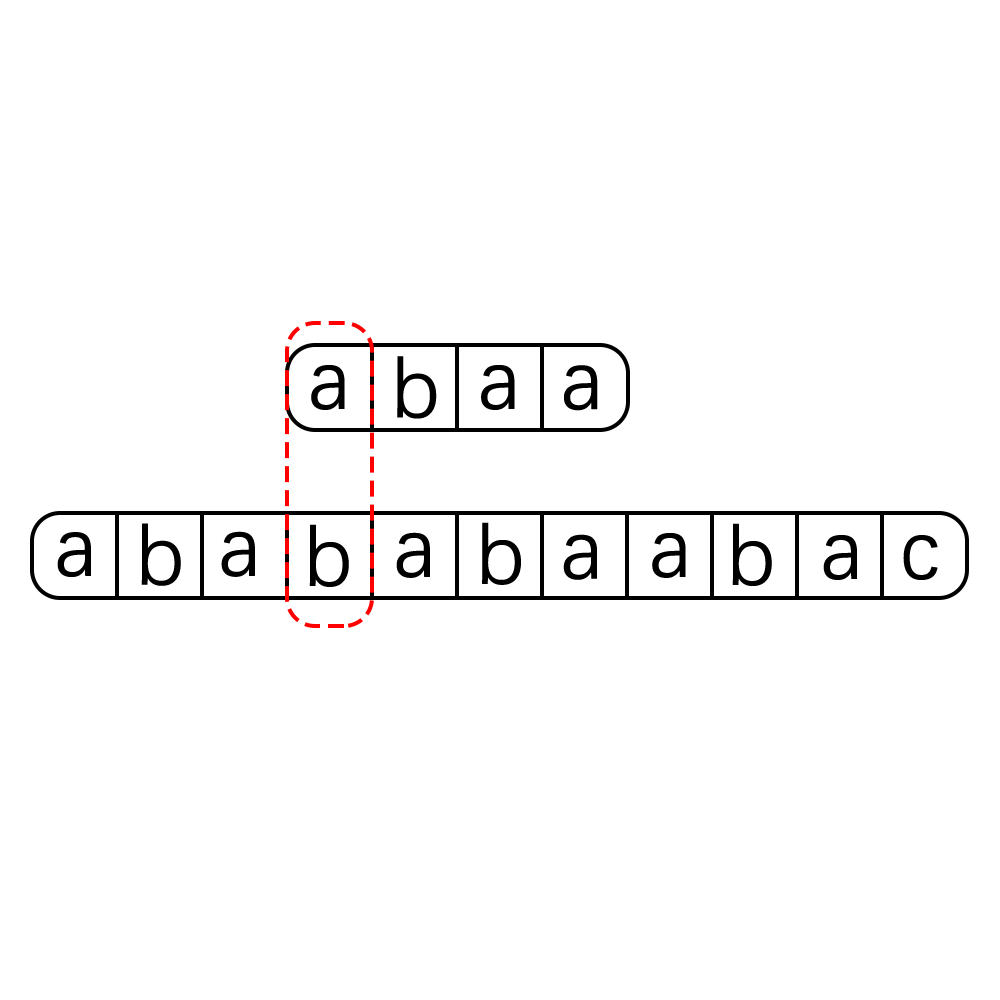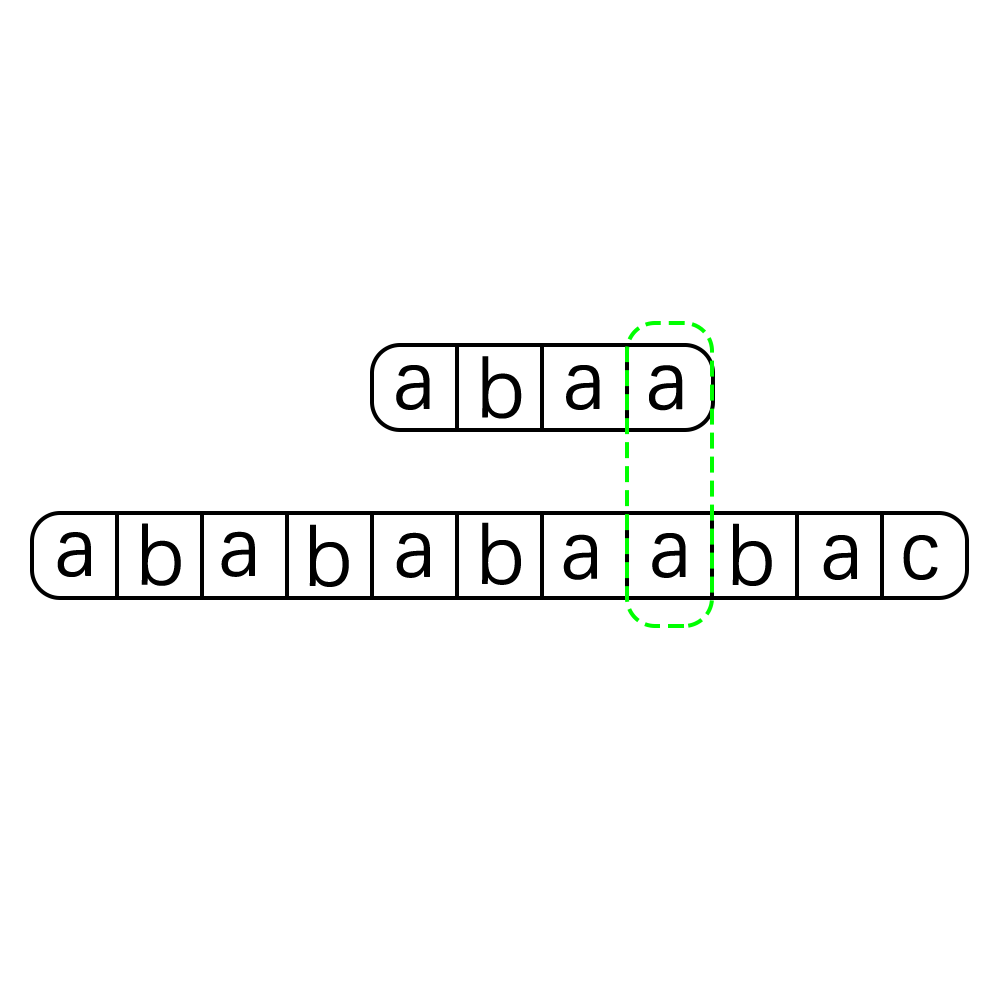
就是这么简单粗暴，这种算法的优点就是简单，还有就是不容易漏错，但是其最致命的一个缺点就是时间开销太大了，一看代码马上就可以分析得出其时间复杂度为O(m*n) m,n分别是str和pattern的长度，当str和pattern的长度都很大时，使用这种算法无疑时灾难，在大数据当道的今天我们要探寻一种更为高效优雅的算法，那就是我们今天的主角KMP算法。

三、KMP算法

• 要想了解KMP算法算法，就要先又字符串前缀和后缀的概念，什么时字符串的前缀和后缀，看看下面的例子相信聪明的你马上就懂了：
  例：字符串 = “abab"

前缀	后缀	长度
a	b	1
ab	ab	2
aba	bab	3

看了例子你因该一目了然什么时字符串的前缀和后缀，现在不妨我们来模拟一下人的思维，以我们人的大脑来处理该怎么匹配两个字符串，请看下面这幅图：

我们可以看到第一次在匹配到 c 的时候我们发生了匹配失败的现象 但是，我们又看到前面已经匹配成功的字符串中 aba 不正是模式串的前缀吗，那我们马上就可以把模式中的前缀aba 移动到于 匹配串的 aba 进行配对，这不就省去了归零这种浪费时间的操作，这里可以看到核心就是利用前面已经匹配过的信息，然后利用它找出下次最佳的开始位置；
我们可以先推岛一下公式，先社模式串为P,匹配串为T，i为当前T的下标，j为当前P的下标：
当发生失配时：

1、我们可以知道 P[ 0 至 j - 1 ] == T [ i - j 至 i - 1 ] 这个表达式是成立的吧

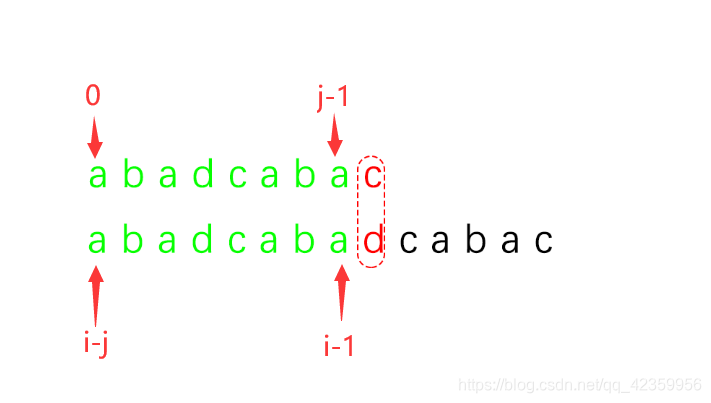
可能看公式没懂，但看上图下应该你就一目了然了。

2、然后我们又来分析这段已经匹配成功的字符串（绿色的这段）的结构：
我们可以发现它有一个很奇特的现象：

也就是字符串的前缀后后缀有相同的地方这里就要引入最大公共串概念

字符串	前缀	后缀	最大公共前后缀长度
a	^	^	0
aa	a	a	1
aba	a,ab	a,ab	2
abcabc	abc	abc	3

那么我们现在又可以推导出一个公式，我们知道P串前部已经匹配成功了的字串为
P[ 0 至 j - 1] ，如果我们假设这个字符串中的最大公共前后缀长度为k，那么是不是有
P[ 0 至 k - 1 ] == P[ j - k 至 j-1] ；
看图：

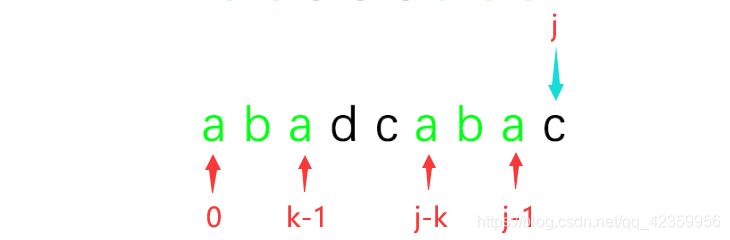
3、有了上面两个推倒出来了公式我们可以把它们联合起来看看，就会得出：

（1）因为 P[ 0 至 j - 1 ] == T [ i - j 至 i - 1 ]
（2）又因为 P[ 0 至 k - 1 ] == P[ j - k 至 j-1 ]
（3）联（1）（2）就有：T[ i - k 至 i -1 ] == P[ 0 至 k-1 ]

还是不理解的可以看下图：

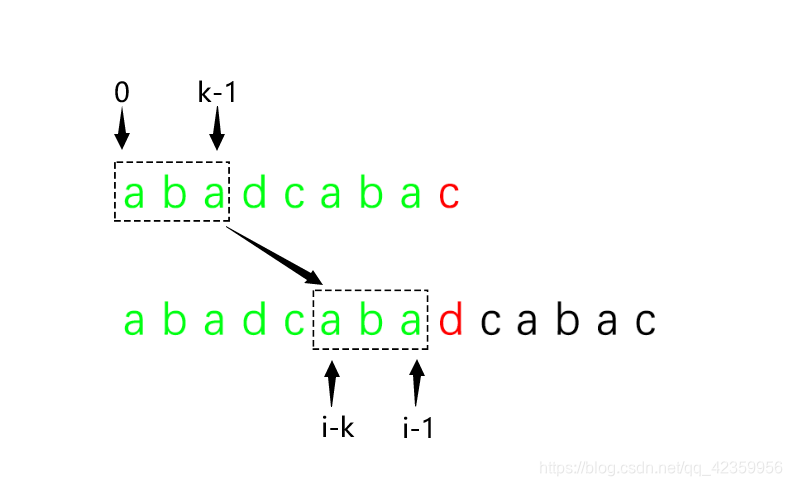
4、经过前三步的推导，原理应该就略知一二了，那么找到了规律，我们在计算机中程序中该如何实现呢？，不知道大家返现没有，其实这种方法唯一和我们开始说到的暴力法不同的地方就是失配环节 i 和 j 的变化不一样；
怎么个不一样法：BF（暴力法）我们在失配时是又将 j 进行归零处理,i 又回到它们已经匹配的子串的头部。
而KMP算法其实就在这里失配时，他的 j 不是置为零，而是变成了k，而这个k就是P[ 0 至 j-1] 这一段中最大公共前后缀的长度；要是我们能把P（pattern模式串）这个字符串的所有位置的 k 都求到那不就行了吗？我们暂且用一个名为 next 的容器来存放这每个位置的 k 值
那么就可以表示为 P(pattern 模式串)的第 j 个位置的K值为 next[ i ];
那么就可以将我们最先写的那个程序改写为：

bool BF(string str,string pattern){
    int i=0,j=0;
    while(i < str.length() && j < pattern.length()){
        if(str[i] == pattern[j]){
            i++;
            j++;
        }else{
        	j = next[j]				// j变next的值，而i不变
        }
    }
    return j == pattern.length();
}

怕有的小伙伴晕，我还是要强调一下next中的k值不是从P[ 0 至 j ] 这一段的， 而它表示的是 P[ 0 至 j-1 ] 这一段的最大公共前后缀长度，一定注意！！！

好了现在的当务之急就变成了next数组的寻找，只要把next数组找到了，那一切就迎刃而解了。

四、寻找next数组

要先寻找next数组，先来将下面这个例子的next数组找出来把，在从中找规律：

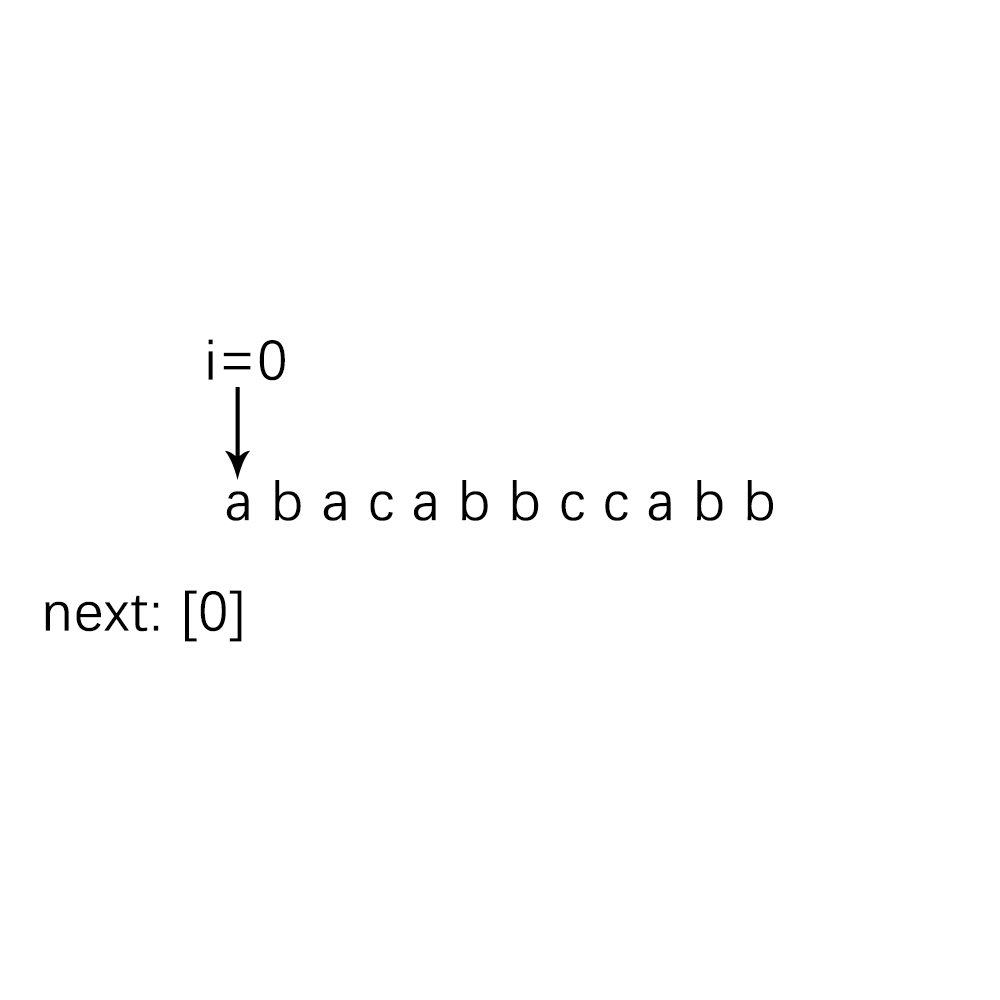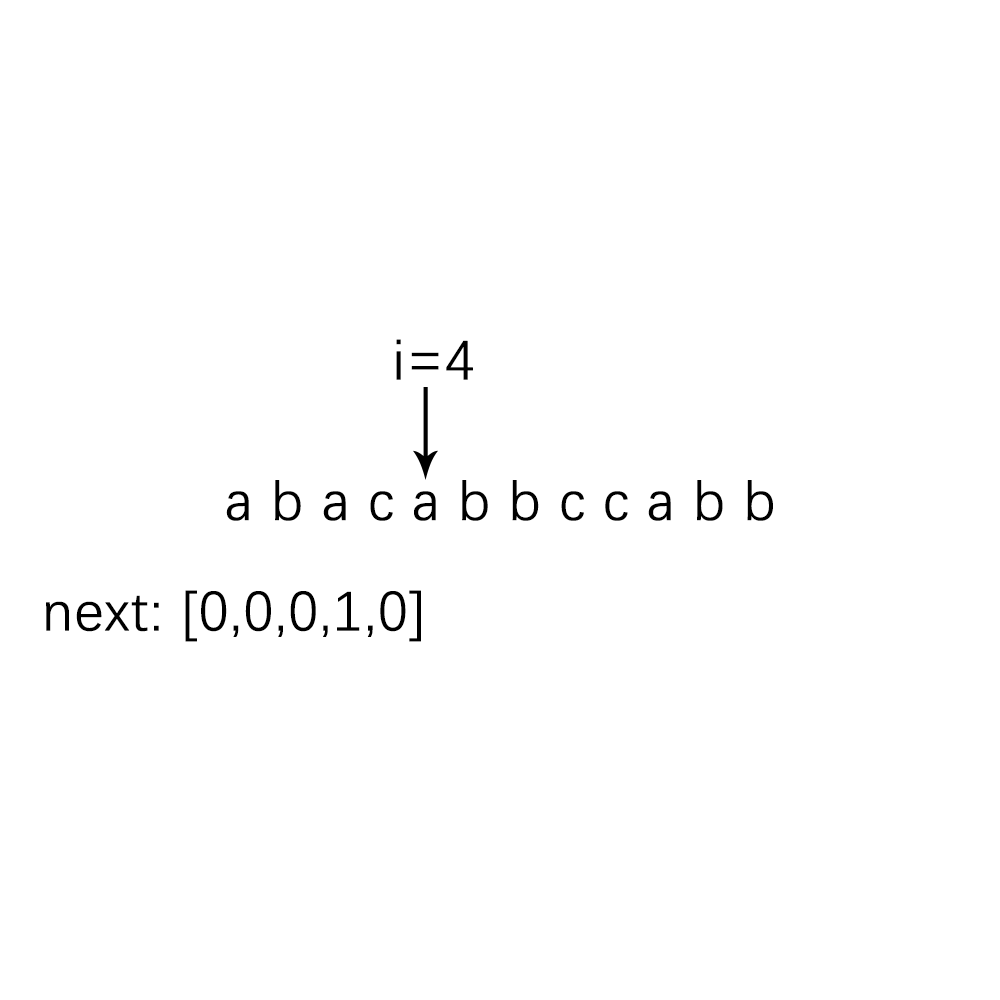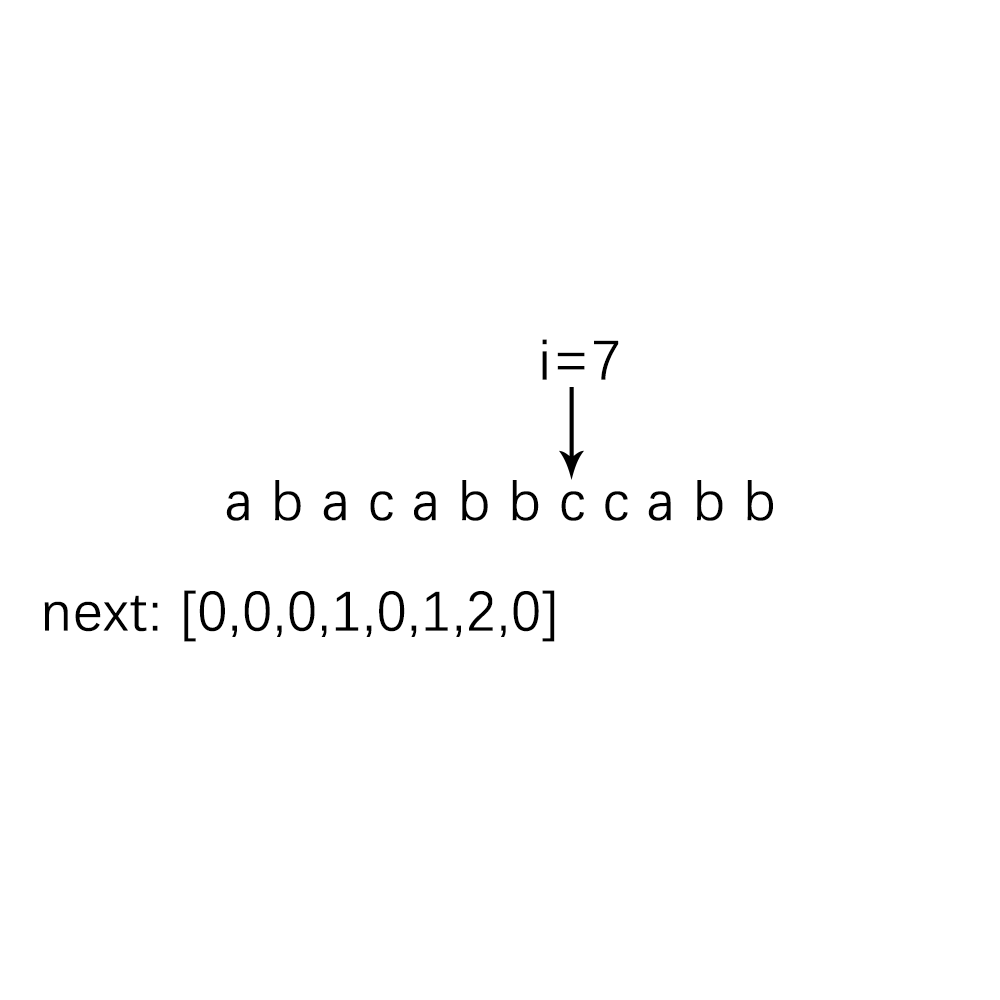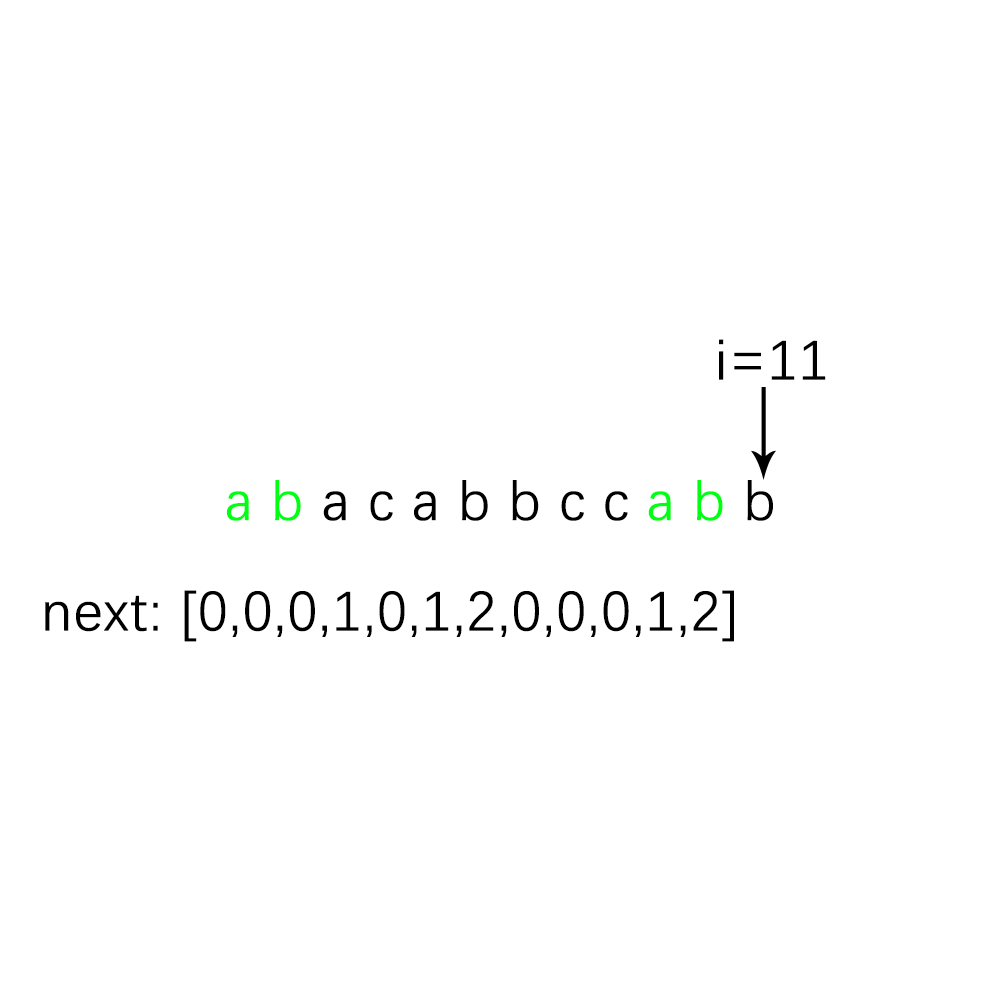
根据我们的人眼不难看出next数组中的值，但是对于程序而言，就需要算法了，不妨我们来分析一下我们人脑探寻next数组值的过程，我把这个求Next数组的过程，归结为了动态规划问题，不懂动态规划也没问题，且看下面的分析：
没学过动态规划的你可以把它拿来当数学归纳法来看：
那么先假设：我们已经求出了next 数组的前 j 位的值，而且next[j] = k那么我们现在就有数组：

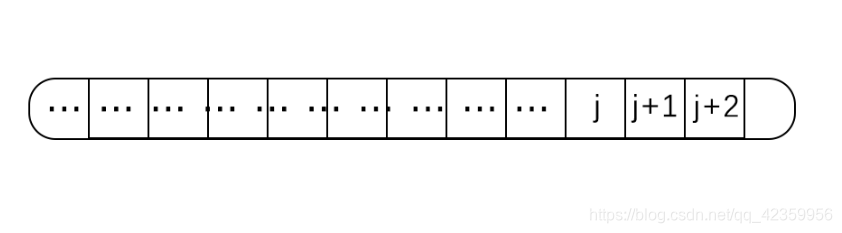
现在我们想要求 j + 1 位该怎么求呢，既然我们都知道 next[ j ] = k ,它表示字符串（0 到 j - 1）
的最大公共前后缀长度为k，那么就有下图：

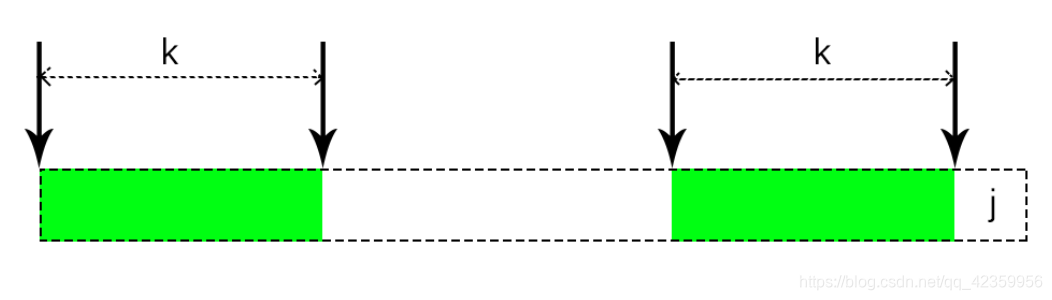
那么我们在求就 j + 1
第一步无非就是求此字符串的第 k + 1个字符是否等于 （j + 1）- 1 个字符，可以理解为下图：

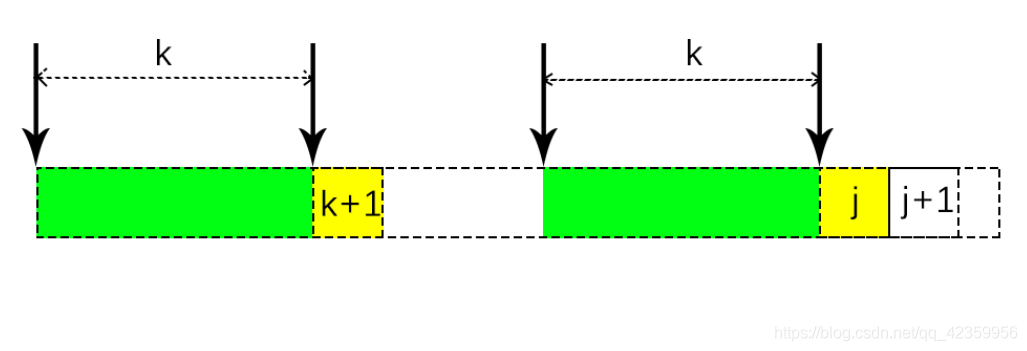
如果字符串中 k + 1位的字符 等于 j 位的字符 那么就有 next[ j + 1 ] = k+1 (也就是图中黄色加绿色的那一部分字符串的长度)
等于的情况下还好理解，要是不等于的时候，next[ j + 1] 又该怎么求呢，不急我们在讨论下种情况时，先把下面这张图看了来：

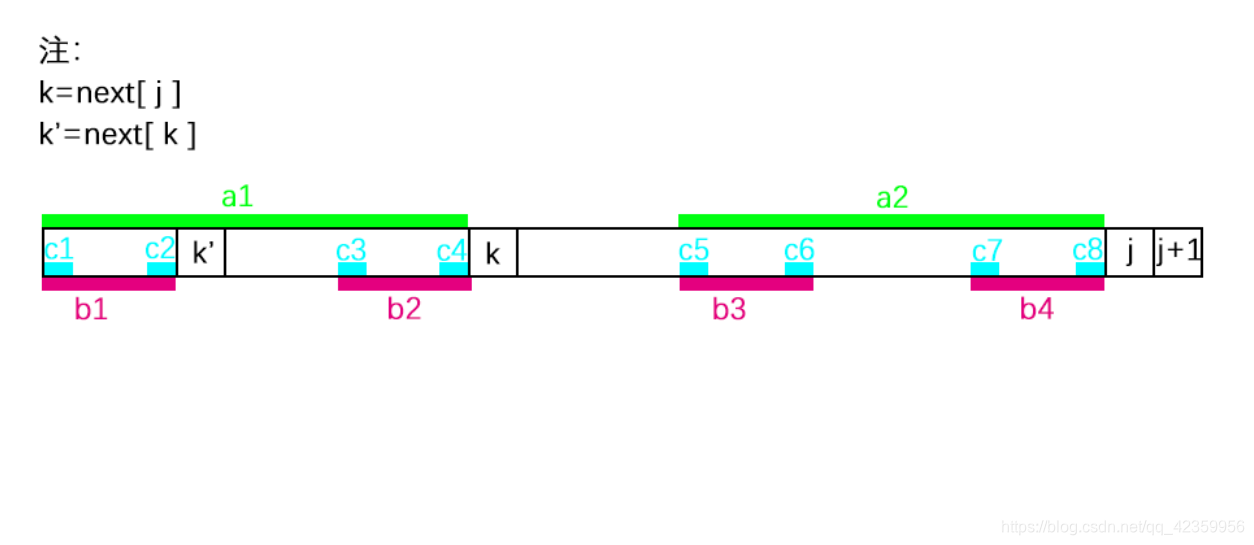
好了有了图我们可以跟着图来推导一下了：

1.设模式串为 P,其next数组已经初始化完成
2.那么就有 k = nex[ j ]，可见图中a1字符串的长度为 k 个长度 ；
因为next数组中的值为 P[ 0 至 j - 1]中的最大相同前后缀长度，那么就有 a1(前缀)= a2(后缀);
3.又有k’ = next[ k ],所以同理可得 b1 = b2,
4.同2和3小点的原理一样 可得 c1的长度为 next[ k’ ]，且 c1 = c2;
5、那么由2，3，4点推出来的式子可得：
∵ b1 = b2;c1 = c2;
∴ c1 = c2 = c3 = c4;
又∵ a1 = a2;
∴b1 = b2 = b3 = b4;
∴ c1 = c2 = c3 = c4 = c5 = c6 = c7 = c8;
整理一下即可得到下面的结果：
(1) a1 = a2;
(2) b1 = b4;
(3) c1 = c8;
…… ，……
(n) n1 = nn;（直到P[0, n-1] 没有公共前后缀了为止 也就是 (next[ n ] = 0 且 n=0) ）
还是不懂的不妨跟着下面的动画再想一下；

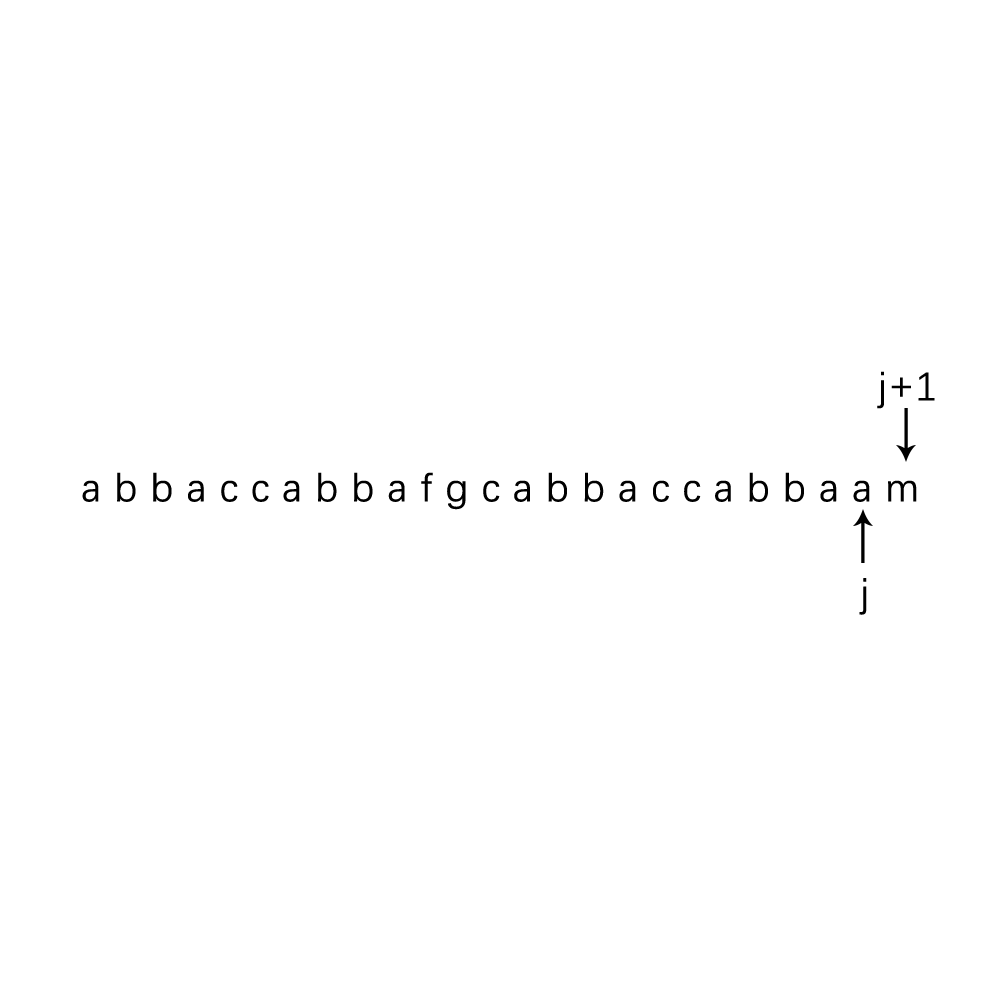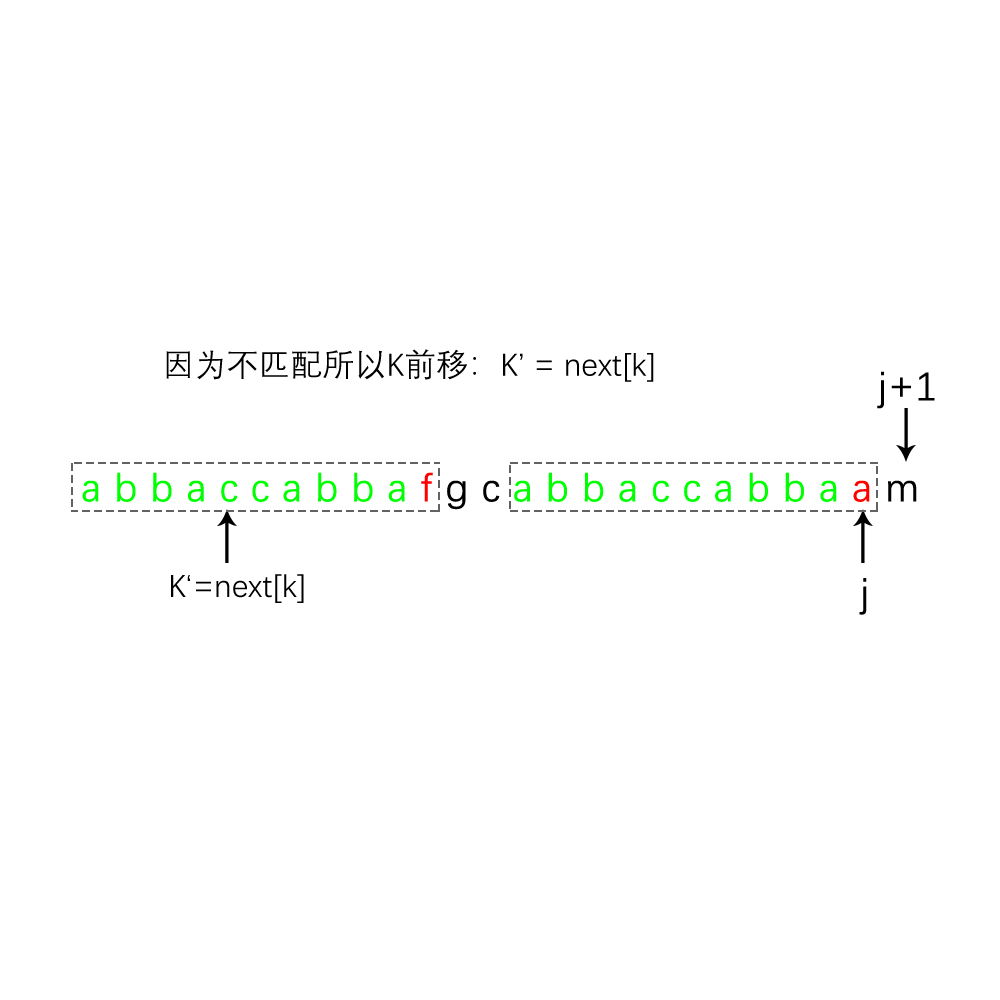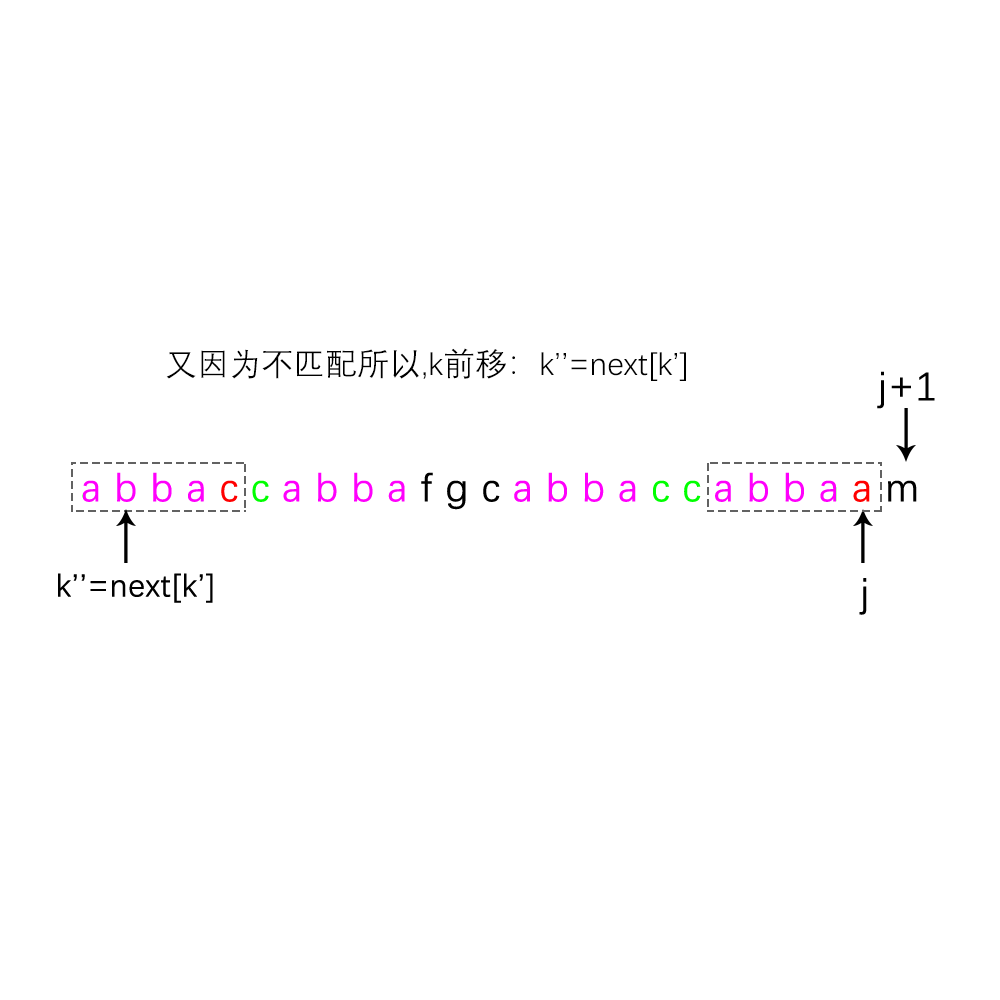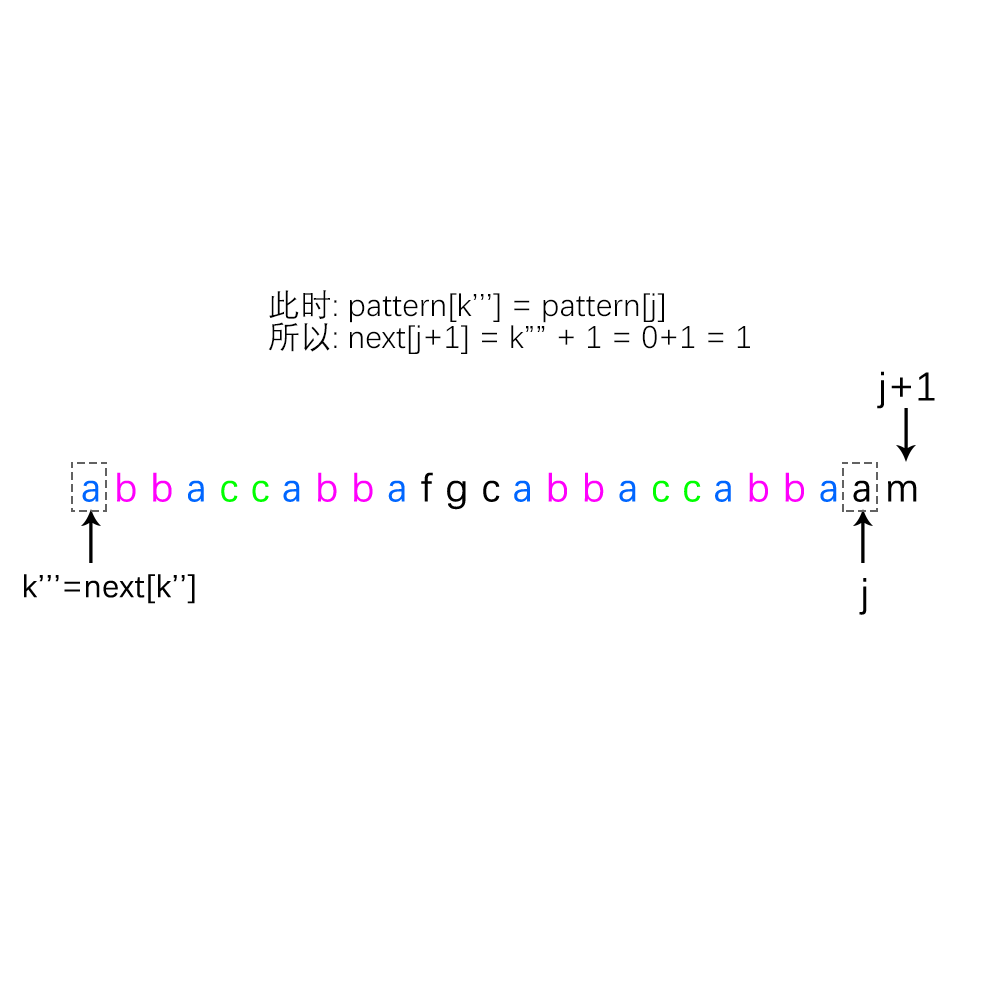
那么我们根据这些规律就可以得出一个初步求next数组的方法，代码如下：

vector<int> initNext(string pattern){
    vector<int> next(pattern.length());
    int k;
    next[0] = 0;

    for(int j=0;j<pattern.length()-1;j++){
        k = next[j];
        
        while((k != 0 || next[k] != 0) && pattern[k] != pattern[j]){ // k不能到达0，且两个下标对应的字符不相等时才能循环
            k = next[k];
        }

        if(pattern[k] == pattern[j] && j != k){  // 两个下标指向的字符相等 且 下标不能一样
            next[j+1] = k+1;
        }else{
            next[j+1] = 0;
        }
    }
    return next;
}

这段代码写得很乱，因为我想尽量满足上面我们分析的那么逻辑来，所以是拼凑出来的，但是以这样的顺序读下来应该要好理解这个next数组的求法。
既然代码看了，这是我们跟着上面分析的思路初步得出的代码，显然要是以上面的方式求nexe的话是不优雅的，那我们再来分析一下上面的代码做一些简化：
首先看这一段：

这里循环前面的一个条件是 k != 0 || next[k] != 0,什么含义呢，不急看图就清楚了：

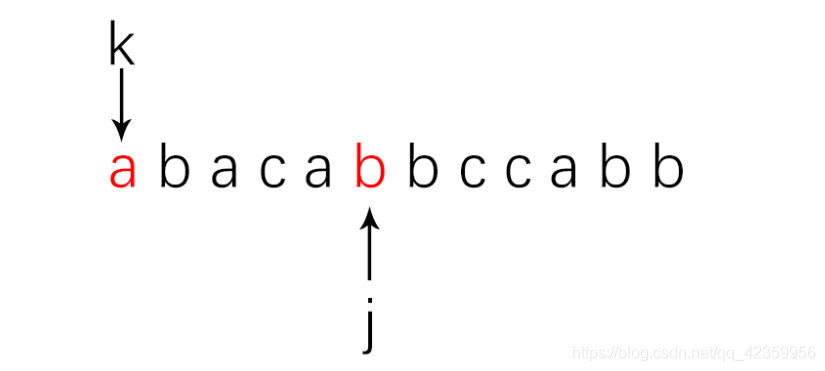
很明显图中已经出现失配的现象了，而且此时的 k = 0,而且 next[k] 后 k 依然还是会等于 0 所以这里要标注一个状态，也就是 k 已经指向 pattern 的头部了，所以我们不妨可以将next数组的0位用一个 -1 来进行标注到头了，代表它前面已经没有了，那么代码就可以简化成：

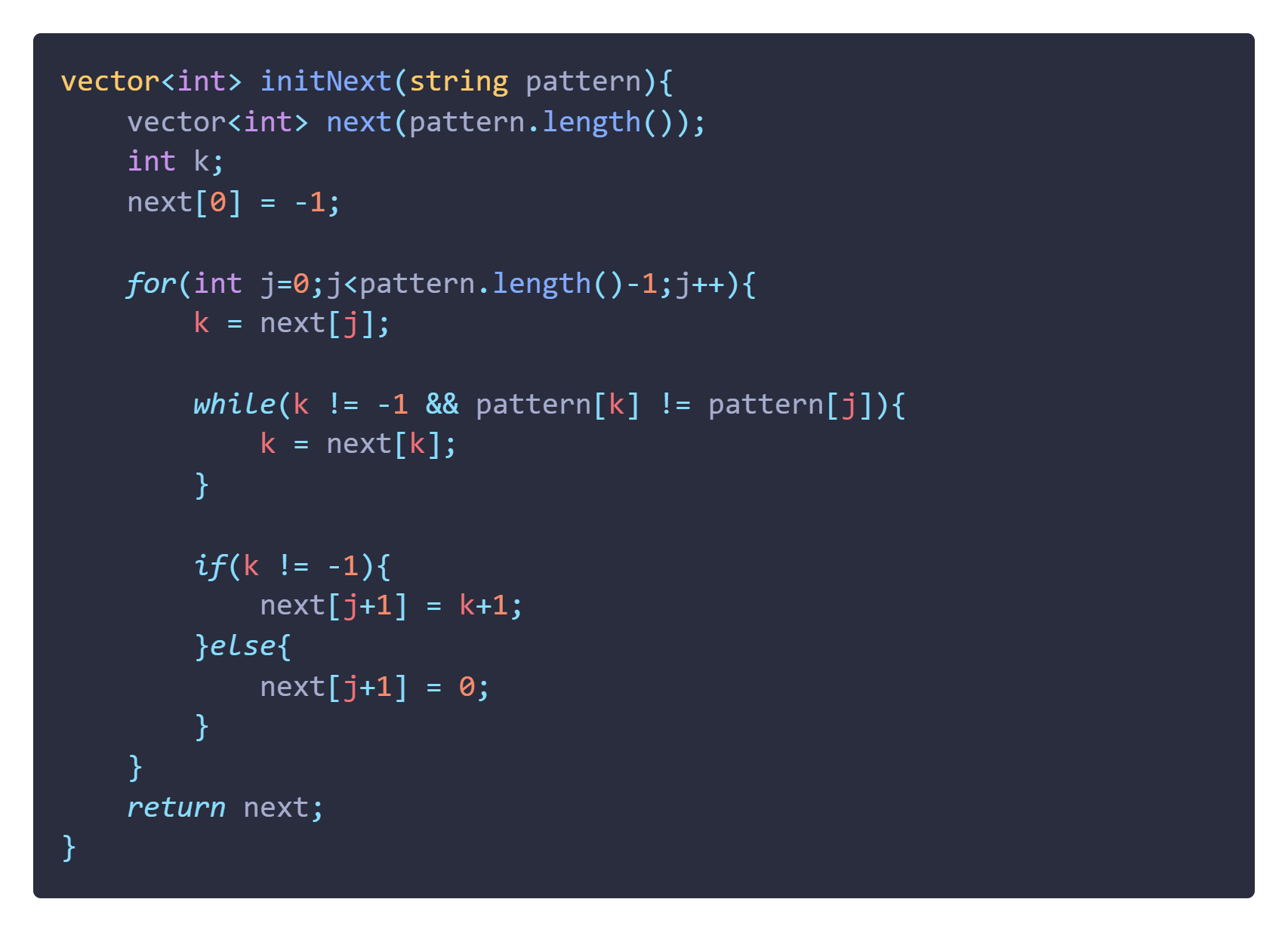
哈哈还是很乱，那再看图中 if 这一块又可以简化：因为如果 k == -1时即会触发else，那么next[ j +1] = 0;
这条语句难道就不等于 next[ j + 1] = k+1 (反正此时k也是-1 加了个1也是等于0)；
于是就变成了下面这样：

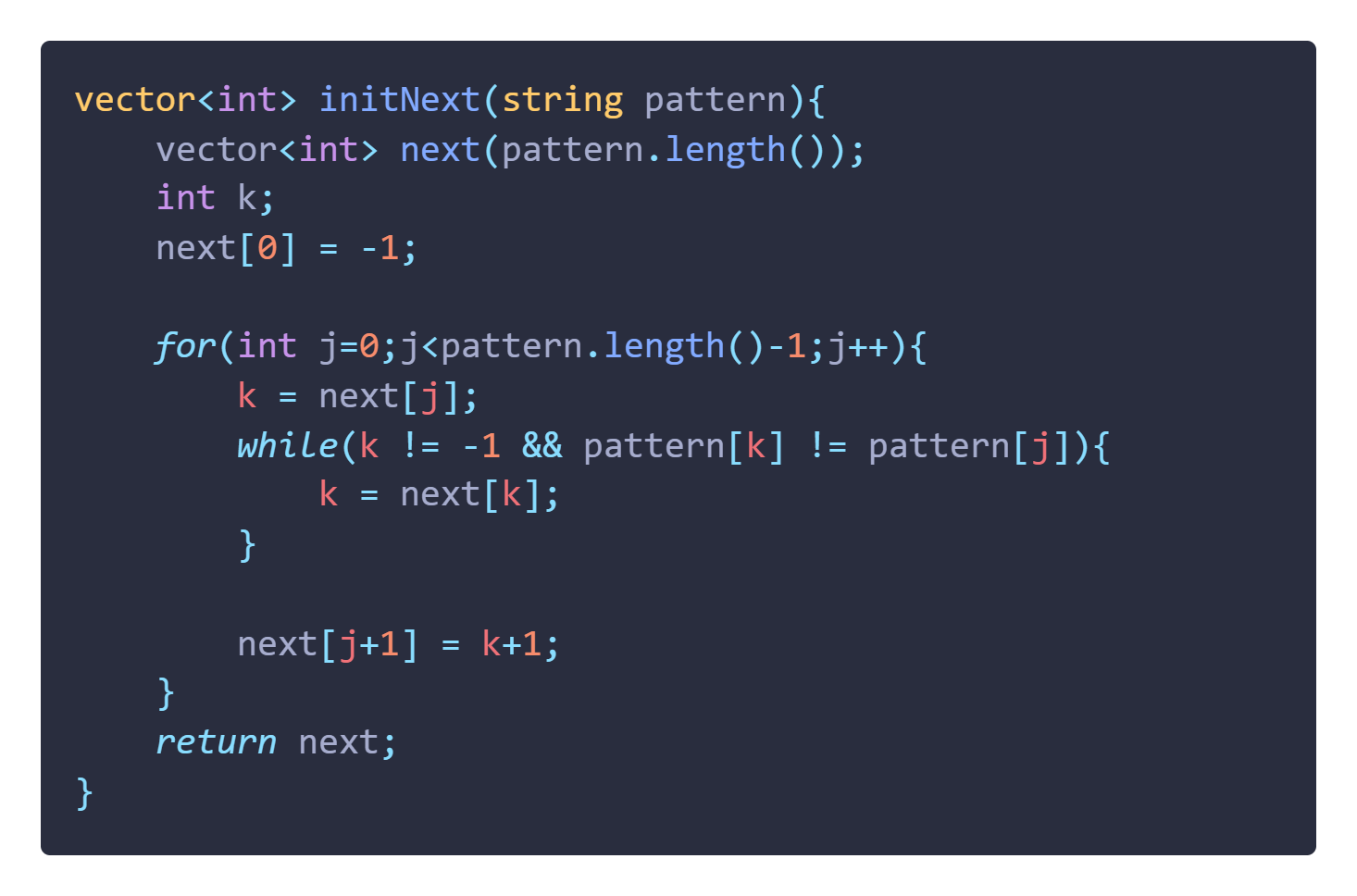
很遗憾还是不行，此处有两个循环，我们要把他压缩成一个才行，我们发现内层循环这个while有个很奇特的地方，那就是如果我们没有匹配上，那么就会一直迭代 K 的值，但是在此过程中我们的 j 是一直没变化的，那我们何不自己手动控制 j 的值？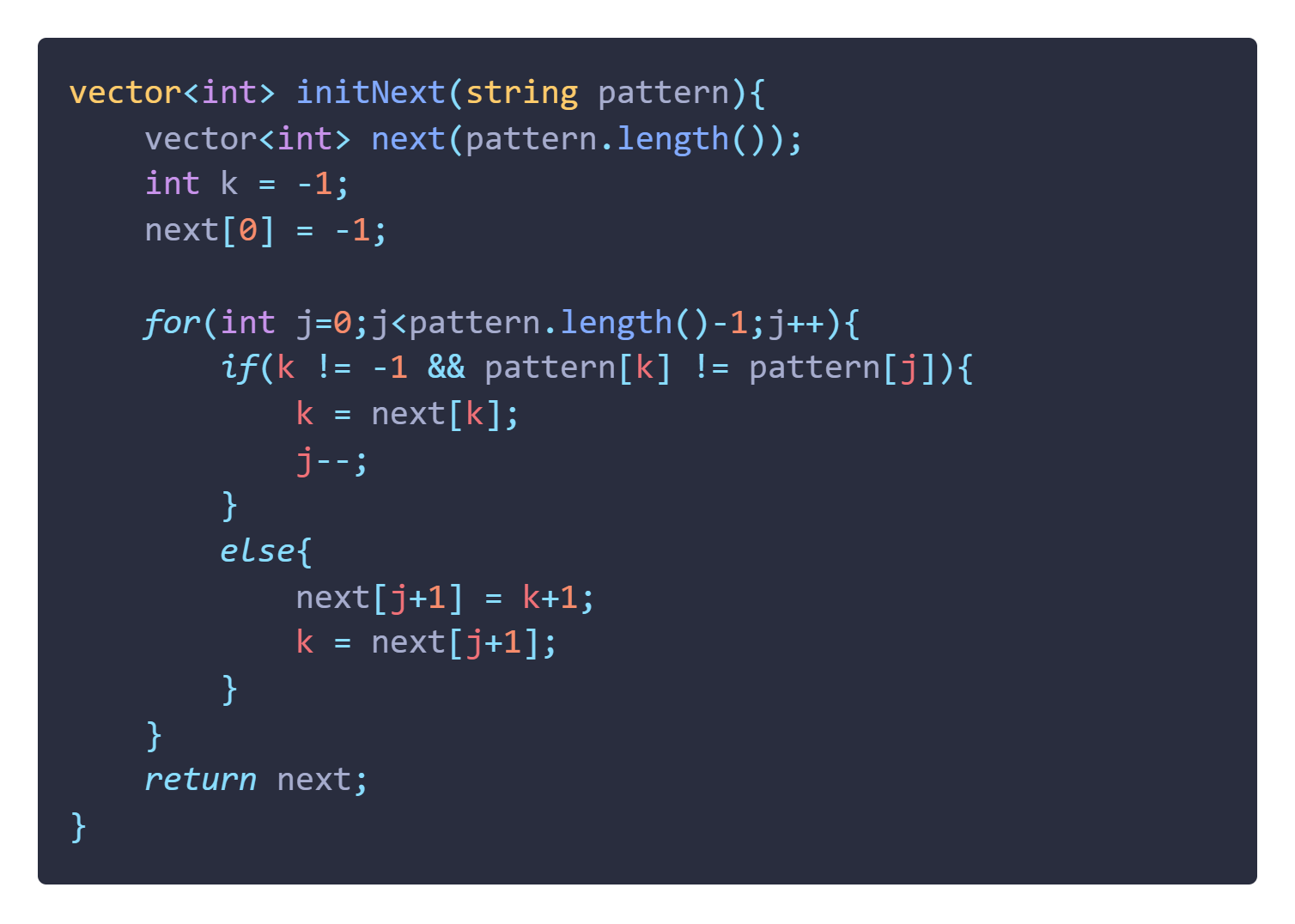
我知道这样做有点傻，但是也是为了过程而过程，（其中的 j- - 是为了抵消掉每次次循环结束后j的自增环节，所以强行使其 j 值不发生变化），可以看到上面的这个代码我们已经将其优化成了一个循环了，
但还是不怎么不美观，最后再整理一下就得到了下面的代码：

vector<int> initNext(string pattern){
    vector<int> next(pattern.length());
    int k=-1,j=0;
    next[0] = -1;

    while(j < pattern.length() - 1){
        if(k == -1 || pattern[k] == pattern[j]){
            next[++j] = ++k;
        }
        else{
            k = next[k];
        }
    }
    return next;
}

这就是大家喜闻乐见的版本了，其实和上图的那个变化就是for变成了while， if 和 else 做了一次取非的处理（也就是反转；

五、最后的处理

经过前面的讲解，你已经知道了KMP算法的原理和next数组的求解，对于精益求精的精神，我们还要对其做最后的处理，因为上面的代码还存在一个BUG，但不致命，且看下面这个匹配案例：

上图的这种情况不难看出，我们在失配时，pattern[ j ] != pattern[ i ]，在这种特殊的匹配串pattern下面，明显这个字符串属于AA型字符串，也就是前半段和后半段一样，也就是说出现：
pattern[ next[ j ] ] = pattern[j] 这么一种情况时：
证明：
∵pattern[ j ] != pattern[ i ]
k = next[j];
以next的性质得：pattern[0:k] == pattern[j-k,j]
又 ∵ pattern[ k ] = pattern[ j ]
∴ pattern[ k ] != pattern[ i ]

那么就清楚了，也就是在这种情况下，我们回退是做得无用功（即时回退到k的位置，但是也不能匹配成功），那我们得在构造next数组时再打上一个补丁：

vector<int> initNext(string pattern){
    vector<int> next(pattern.length());
    int k=-1,j=0;
    next[0] = -1;

    while(j < pattern.length() - 1){
        if(k == -1 || pattern[k] == pattern[j]){
            if(pattern[++j] == pattern[++k]){
                next[j] = next[k];
            }else{
                next[j] = k;
            }
        }
        else{
            k = next[k];
        }
    }
    return next;
}

bool serarch(string pattern,string text){
    vector<int> next = initNext(pattern);
    int i=0,j=0;
    const int pLen = pattern.length();
    const int tLen = text.length();

    while((j < pLen) && (i < tLen)){
        if(j == -1 || text[i] == pattern[j]){
            i++;
            j++;
        }
        else{
            j = next[j];
        }
    }
    return j == pLen;
}

• 结束语：
  可以看到KMP算法除去next数组构造的时间，时间负载度可以达到O(n+m),与暴力的手法形成天壤之别；其实在万千匹配算法当中，KMP算法也不过是沧海一粟，算法没有好坏，只有用对与用错之分，不同的算法运用场景不同，如果你对字符串匹配算法很感兴趣，不妨再去看看sunday算法，反正学海无涯苦作舟吧，要学的还有很多，加油吧骚年！

哎~作图不易，如果这篇文章对你有帮助就点个赞再走呗，还有问题得小伙伴可以私聊或者评论区留言讨论；