深度学习（四）：梯度下降法

1.梯度下降法公式原理推导

以二分类问题为例，误差函数：E=(-1/m)×∑[y_i×In(σ(Wx⁽ⁱ⁾+b))+(1-y_i)×In(1-σ(Wx⁽ⁱ⁾+b))]，是关于权重W的函数(输入数据x是已知的固定数据)，我们通过调整权重以达到最小化误差函数的目的。
为了最小化误差函数需要使用梯度下降法：梯度∇E是误差函数增长最快的方向，如果沿梯度的反方向就是误差函数下降最快的方向。计算 E 在单个样本点 x 时的梯度（偏导数）需要知道：
（1）σ′(x)=σ(x)(1−σ(x))
推导过程：

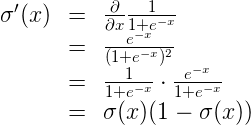
（2）如果有 m 个样本点，分别为x⁽¹⁾、x⁽²⁾、… x^(m)，（其中 x 包含 n 个特征，即x = (x₁，x₂，x₃，… x_n)
第i个样本点的预测 y_i^ =σ(Wxⁱ+b)=σ(W₁xⁱ₁+W₂xⁱ₂ … W_nxⁱ_n+b)
则误差函数E=(-1/m)×∑[y_i×In(y_i^ )+(1-y_i)×In(1-σ(y_i^))]，其中i=1,2，… m
所以误差函数的梯度∇E=(∂E/∂w₁， ∂E/∂w₂，… ∂E/∂w_n，∂E/∂b)，即误差函数相对权重和偏差的偏导数组成的矢量。
（3）为此，首先要计算∂y/∂w_j

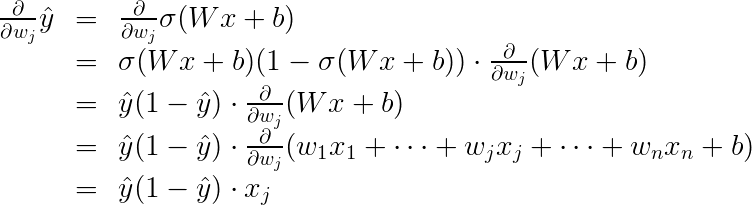
则∂E/∂w_j为

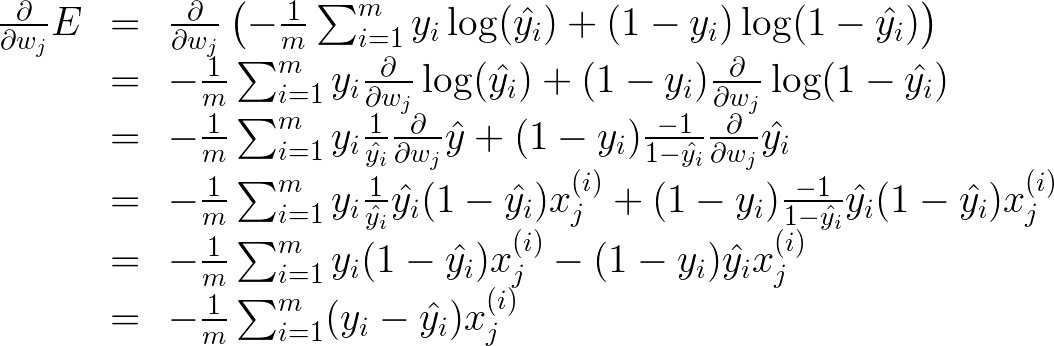
类似的计算将得出：针对单个样本点时，E 对 b 求偏导的公式为：∂E/∂b=−(y− y^)；对于全部样本点，∂E/∂b=(-1/m)∑(y_i− y_i^)
这里得出重要的规则：对于具有坐标x = (x₁，x₂，x₃，… x_n)的样本点，标签 y， 预测y^
该点的误差函数梯度是（ -(y-y^)x₁， -(y-y^)x₂，… -(y-y^)x_n，−(y− y^) ） 即∇E（W，b）= -(y-y^)×(x₁，x₂， … x_n，1)
（4）仔细思考可以发现：梯度实际上是标量乘以点的坐标，标量就是标签和预测之间的差别，这意味着，如果标签与预测接近（表示点分类正确），该梯度将很小，如果标签与预测差别很大（表示点分类错误），那么此梯度将很大。小的梯度表示我们将稍微修改下坐标，大的梯度表示我们将大幅度修改坐标。
为了不引起剧烈的变化，引入学习速率α=0.1，对于每一个样本点用梯度×α来依次更新权重和偏差，对于坐标x = (x₁，x₂，x₃，… x_n)的样本点，偏导数已知，即：
W_i’=W_i - α×∂E/∂W_i
b‘=b - α×∂E/∂b
重复若干epoch，直到误差很小。

​