笔记：网络流-基本知识

容量网络的定义

设一个有向连通图\(N=\langle V,E\rangle\)，记\(n=|V|,m=|E|\).

·容量：每条边\(\langle i,j\rangle\)都对应一个非负实数\(c(i,j)\)

·\(N\)有两个特殊顶点\(s\)和\(t\)，\(s\)称作发点（或源，Source），\(t\)称作收点（或汇，Termination）.其余的顶点称作中间节点。

·称\(N\)为容量网络，记作\(N=\langle V,E,c,s,t\rangle\).

容量网络上的可行流与最大流

设\(f:E\rightarrow \mathbb{R} ^*\)，其中\(\mathbb{R} ^*\)为非负实数集

容量限制

\[\forall \langle i,j \rangle \in E,\ f(i,j)\le c(i,j) \]

平衡条件

\[\forall i\in V-\{s,t\}\\ \sum_{\langle j,i\rangle \in E}f(j,i)=\sum_{\langle i,j\rangle \in E}f(i,j) \]

满足以上条件的，称\(f\)是\(N\)上的一个可行流。称发点\(s\)的净流出量为\(f\)的流量，记作\(v(f)\)，即：

\[v(f)=\sum_{\langle s,j\rangle \in E}f(s,j)-\sum_{\langle j,s\rangle \in E}f(j,s) \]

最大流

流量最大的可行流称作最大流，求给定容量网络\(N\)上的最大流\(f^*\)的问题，称作最大流问题。

网络流建模

多源/多汇问题

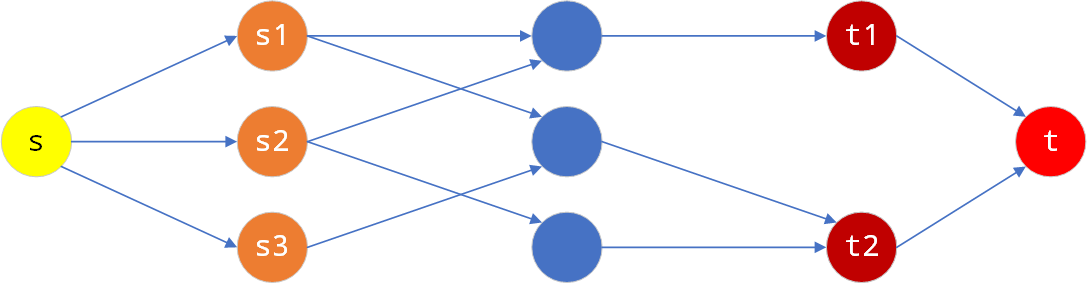
具有多个源和多个汇的网络，可以通过在源之前（或者汇之后）添加一个节点的方式转换为单源单汇问题，如下图

正向边反向边共存问题

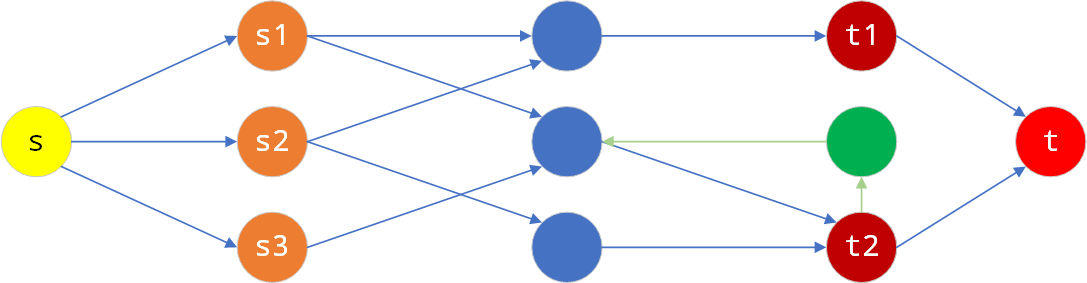
如果两个顶点之间有方向相反的两条边连接，可以在其中一条边上增加一个顶点（如下图绿色顶点），这样可以保证每两个顶点之间只有一条边。

最大流问题的线性规划表述

一个最大流问题可以描述成如下的LP模型

\[\max \ v(f)\\ {\rm s.t.}\quad\quad f(i,j)\le c(i,j),\ \ \langle i,j\rangle \in E \\ \sum_{\langle j,i\rangle \in E}f(j,i)-\sum_{\langle i,j\rangle \in E}f(i,j)=0,\ \ \forall i\in V-\{s,t\}\\ v(f)-\sum_{\langle s,j\rangle \in E}f(s,j)+\sum_{\langle j,s\rangle \in E}f(j,s)=0,\ \ f(i,j)\ge 0,\ \ \langle i,j\rangle \in E \\ v(f)\ge 0 \]

割集、割集的容量、最小割集

设容量网络\(N=\langle V,E,c,s,t\rangle，A\subset V\)且\(s\in A,\ t\in \overline A\)，称:

\[(A,\overline A)=\{\langle i，j\rangle|\langle i，j\rangle\in E且i\in A,j\in \overline A\} \]

为\(N\)的割集；割集可以这么理解：将这个网络划分为两个部分，源\(s\)位于其中一个部分，汇\(t\)位于另一部分，而这两个部分相互不连通，为了使这两部分不连通所需要砍掉的边构成的集合就是割集。

称：

\[c(A,\overline A)=\sum_{\langle i,j\rangle \in (A,\overline A)}c(i,j) \]

为割集\((A,\overline A)\)的容量。容量最小的割集称作最小割集。