无人驾驶5： 贝叶斯公式

假设有个一维的方格，初始位置为均匀分布(因为不知道任何信息)

测量更新

测量当前方格颜色之后，计算所有方格概率分布

#Modify your code so that it normalizes the output for 
#the function sense. This means that the entries in q 
#should sum to one.

p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
Z = 'red'
pHit = 0.6
pMiss = 0.2

def sense(p, Z):
    q=[]
    for i in range(len(p)):
        hit = (Z == world[i])
        q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
    s=sum(q)
    for i in range(len(q)):
        q[i] = q[i]/s
    return q
print(sense(p,Z))

[0.1111111111111111, 0.3333333333333332, 0.3333333333333332, 0.1111111111111111, 0.1111111111111111]

运动更新

假设移动一步，重新计算方格概率分布

p=[0.2, 0.2, 0.2, 0.2, 0.2]
def move(p, U):
    #
    #ADD CODE HERE
    #
    q = []
    if U<0:
        U = U+len(p)
    num = U%len(p)
    for i in range(len(p)-num,len(p)):
        q.append(p[i])
    for i in range(len(p)-num):
        q.append(p[i])
    return q

print(move(p, 1))

[0.2, 0.2, 0.2, 0.2, 0.2]

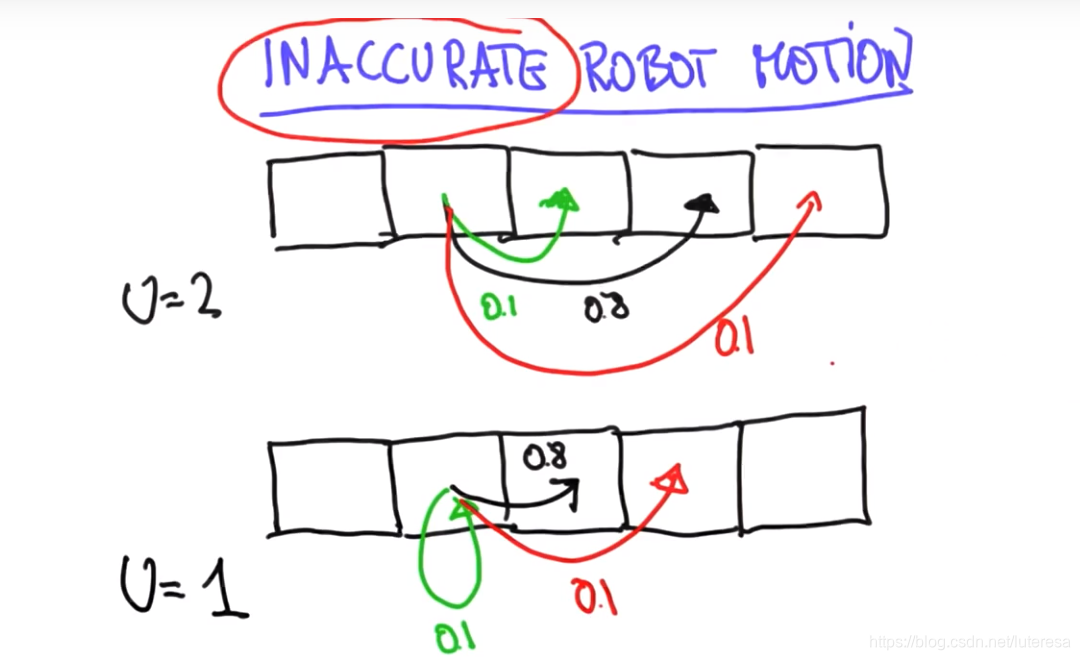
非准确的移动

实际的运动，不太会是完美的运动学，受外部或自身因素影响，会存在一定概率偏差(比如路滑，或者风)

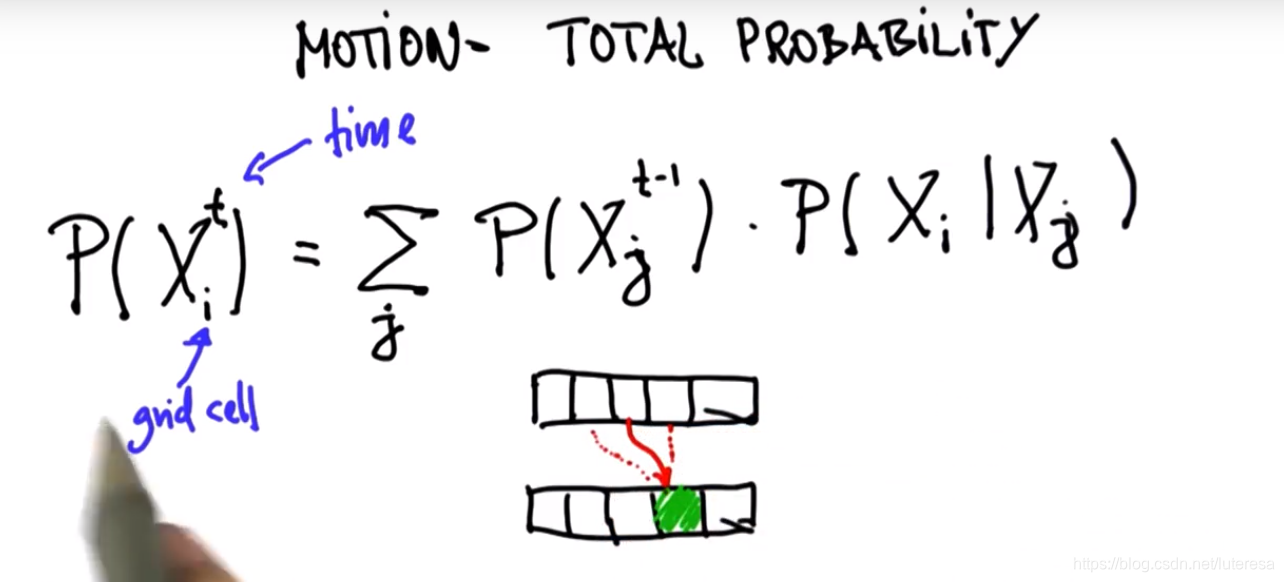
计算概率方式：全概率公式

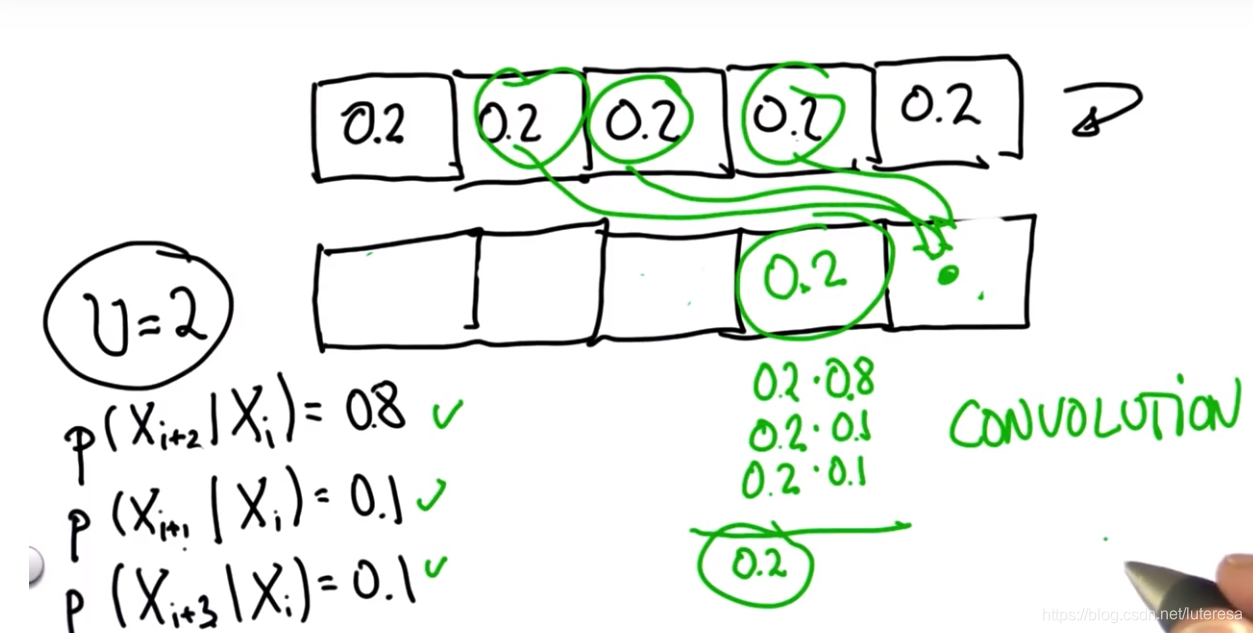
#Modify the move function to accommodate the added 
#probabilities of overshooting or undershooting 
#the intended destination.

p=[0, 1, 0, 0, 0]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1

def sense(p, Z):
    q=[]
    for i in range(len(p)):
        hit = (Z == world[i])
        q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
    s = sum(q)
    for i in range(len(q)):
        q[i] = q[i] / s
    return q

def move(p, U):
    q = []
    for i in range(len(p)):
        q.append(p[(i-U)%len(p)]*pExact+p[(i-U-1)%len(p)]*pOvershoot+p[(i-U+1)%len(p)]*pUndershoot)
    return q
    

print(move(p, 1))

[0.0, 0.1, 0.8, 0.1, 0.0]

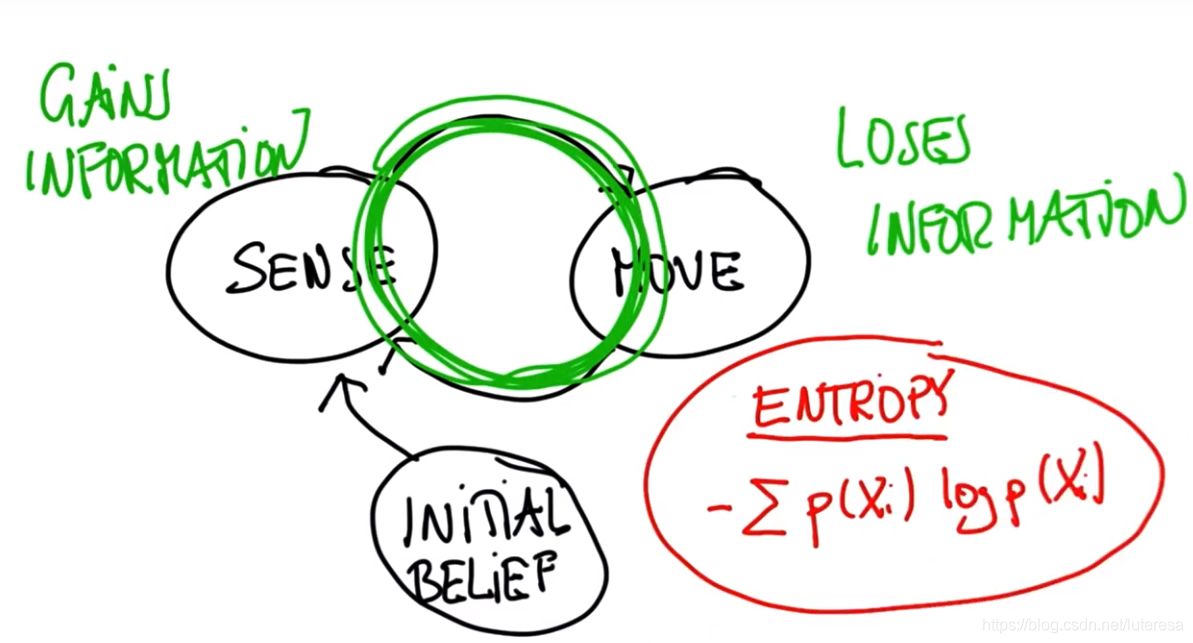
贝叶斯公式模型

包含两个部分，测量更新和预测更新：

测量更新：提高准确性(因为获得准确信息，测量值)，用贝叶斯公式；

运动更新：一般是用运动模型来预测，会降低准确性(运动会有误差，丢失信息)，用全概率公式；

贝叶斯模型，就是测量更新和运动更新的不停循环。

#Given the list motions=[1,1] which means the robot 
#moves right and then right again, compute the posterior 
#distribution if the robot first senses red, then moves 
#right one, then senses green, then moves right again, 
#starting with a uniform prior distribution.

#Modify the previous code so that the robot senses red twice.

p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'red']
motions = [1,1]
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1

def sense(p, Z):
    q=[]
    for i in range(len(p)):
        hit = (Z == world[i])
        q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
    s = sum(q)
    for i in range(len(q)):
        q[i] = q[i] / s
    return q

def move(p, U):
    q = []
    for i in range(len(p)):
        s = pExact * p[(i-U) % len(p)]
        s = s + pOvershoot * p[(i-U-1) % len(p)]
        s = s + pUndershoot * p[(i-U+1) % len(p)]
        q.append(s)
    return q

for k in range(len(measurements)):
    p = sense(p, measurements[k])
    p = move(p, motions[k])
    
print(p)       

[0.07882352941176471, 0.07529411764705884, 0.22470588235294123, 0.4329411764705882, 0.18823529411764706]

贝叶斯模型的数学原理

定义初始分布为先验概率X，测量值为后验概率Z

测量更新，即求p(x|z)

$p(x_i|z) = \frac{p(z|x_i)p(x_i)}{p(z)}$

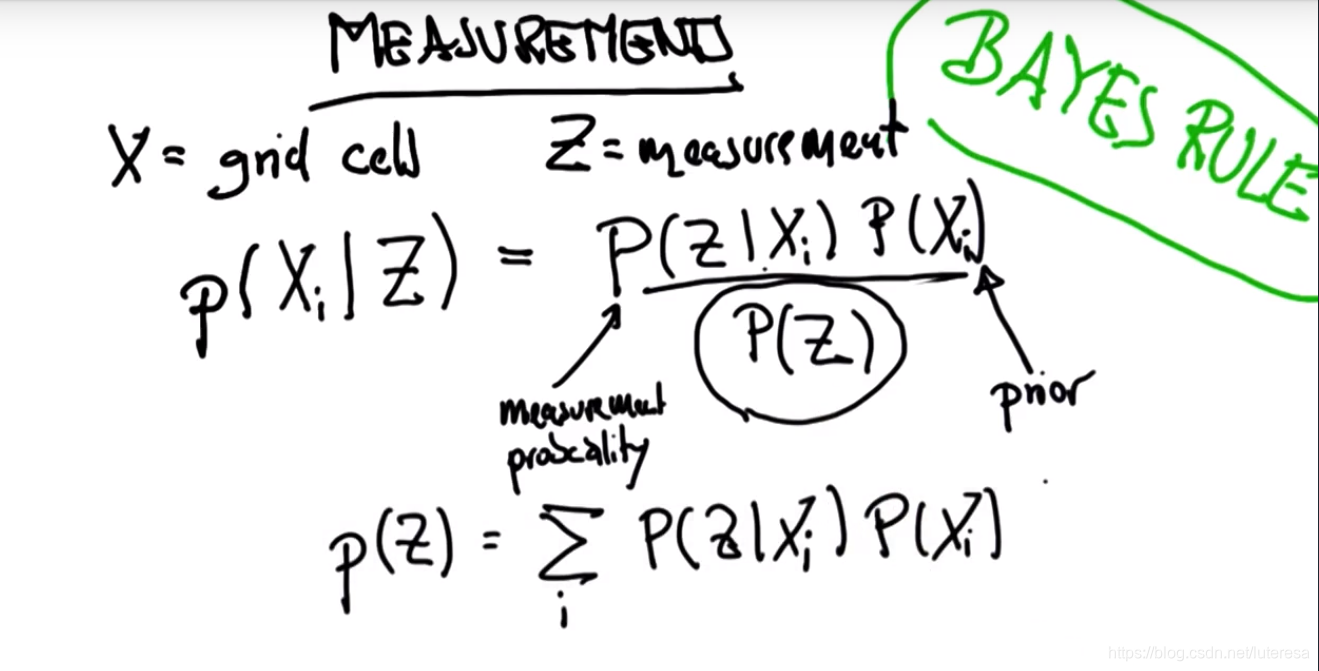
运动更新由全概率公式计算：

$p(x_i^t) = \sum_{j=1}^{n}{p(x_j^{t-1})p(x_i|x_j)}$