理论
Hammersley采样
在图形学里面,用到了很多的采样算法。特别当你在写一个光线追踪器的时候,会使用大量的采样算法来对BRDF,光源等进行采样。这些采样操作,一般是先通过创建一个具有均匀分布的2D随机点集合,然后通过变换,将这些2D随机点变换到具体的采样数据上去,如BRDF的方向等等。其中经常被使用到的均匀分布的2D随机采样方式–Hammersley采样。
Hammersley采样,听上去好像很深奥的样子,实际上是一个十分简单的操作。
我们知道,在计算机里面大量使用了二进制来表示数据,如下表所示的一些十进制与二进制的对应关系:
| 十进制 | 二进制 |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
而Hammersley采样就是利用计算机使用二进制表示的特性,来构造均匀分布的2D随机采样点。它是通过对一个二进制数进行Radical Inverse方法,来构造出一个值来实现的。它的过程如下表:
| 十进制 | 二进制 | Radical Inverse | 值 |
|---|---|---|---|
| 1 | 1 | .1 = 1 * 1/2 | 0.5 |
| 2 | 10 | .01 = 0 * 1/2 + 1 * 1/4 | 0.25 |
| 3 | 11 | .11 = 1 * 1/2 + 1 * 1/4 | 0.75 |
| 4 | 100 | .001 = 0 * 1/2 + 0 * 1/4 + 1 * 1/8 | 0.125 |
从上表可以看到,Radical Inverse方法,就是简单的将给定的十进制数的二进制表示方法,反过来放在小数点之后,构造一个在[0,1]之间的值。
在明白了Radical Inverse方法之后,我们就可以构造hammersley的2D随机分布的采样点集合,如下所示:
其中N表示的是一共有多少个采样点,$ \phi(i) $ 就是对i进行Radical Inverse之后的值。
对应的分布图如下所示:

引擎里对应的分别给出支持位运算和低阶实现的GLSL代码:
// 位运算
float RadicalInverse_VdC(uint bits)
{
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// 不支持位运算
float VanDerCorpus(uint n, uint base)
{
float invBase = 1.0 / float(base);
float denom = 1.0;
float result = 0.0;
for(uint i = 0u; i < 32u; ++i)
{
if(n > 0u)
{
denom = mod(float(n), 2.0);
result += denom * invBase;
invBase = invBase / 2.0;
n = uint(float(n) / 2.0);
}
}
return result;
}
蒙特卡罗尔积分(Monte Carlo Integration)
蒙特卡洛积分主要出现在统计和概率学理论中。
举一个例子:假如你想统计某个国家公民的平均身高。为了得到你的答案,你可以测量每个人的身高并取平均值最后得到十分准确的答案。当然,这种方法十分耗时耗力,所以我们会采取更为方便但结果不是很精确的方法。
我们可以在这些人口中完全随机的测量一定人数的身高并获得平均结果。人数可以小到只测量100人的身高。这样你可得到一个比较准确的结果,这被称之为大数定律。具体而言就是,只要做到真正的随机选取一个集合中的子集合进行测量,你就能得到非常接近最终答案的答案,而答案的精确度随着子集合的大小而增加。
蒙特卡洛积分建立在这个大数定律的基础之上,并且使用同样的方法来解决积分。不使用所有可能的采样值X来计算积分,而是生成几个随机采样值N来解决积分。随着N的增加我们会获得更加接近准确答案的结果。
为了解决这个积分,我们在区间a到b中随机选取N个采样向量,求它们的和并最后除以采样的数量。pdf是可能性密度函数,它告诉我们在总采样向量集合中选取某个特定的采样向量的概率。举一个例子:人群身高的pdf看起来是这个样子

从这幅图片可以看出如果我们对人群随机采样身高,有很高的概率得到1.70,很低的概率得到1.50。
根据蒙特卡洛积分,一些采样值可能会有比其他采样值更高的生成概率。这就是为什么对于任意的蒙特卡洛估计值,我们要除以或者乘上该采样向量的概率值即pdf函数值。到目前为止,对于估算积分的每种情况,我们生成的采样都是统一的,都有相同的生成概率。我们的估计值直到现在都是公平的,这意味着给一个数量不断增长的采样,我们最终会收敛到一个准确的积分值。
当然,一些蒙特卡洛估量是不公平的,这意味着生成采样向量的时候不是完全随机的,而是聚集在某个特殊的值或方向附近。这些非公平的蒙特卡洛估量有着更快的收敛速度,这意味着它们能够非常快的收敛到准确答案,但是由于它们不公正的天性,它们并不是总能收敛到准确答案。这往往意味着需要一个可接受的权衡,特别是在计算机图形当中,准确的答案对结果并不是特别重要。
蒙特卡洛积分在计算机图形学中十分流行,因为它使用一种相当直观的方式来近似获取连续积分的结果:在任何地方/体积中进行采样(比如半球体Ω),生成N个随机采样,计算并权衡每个采样对最终结果的贡献。
重要性采样
概率密度
对于连续型随机变量来说,概率密度函数就是描述了在样本区间里面子区间发生概率的一种函数,它和随机变量X的关系如下所示:
。其中 表示的就是事件发生在样本区间 中的概率。而 就是随机变量 的概率分布函数。所以随机变量 和概率密度函数 之间就是积分关系。这也就说明了,对于单一事件发生的概率在该积分中是没有意义的。
除了上面的公式之外,概率密度函数还有一个重要的特性:
这个特性表示,事件发生在整个概率区间里面的概率为1。
其中 就是概率密度函数。这里之所以要除以 ,是因为当我们的采样点为 的时候,我们可以通过 计算出该采样点对最终积分的一个贡献度权重值,这样一除就能够得到最终的积分值。
细心的读者可能会发现,好像我们只要找到一个采样点 ,然后求出 和 ,在使用 就已经能够得到最终的积分值了啊,干么还要采样那么多的数据,然后在求个平均值?这是因为,在解决实际问题的时候,我们往往很难精确的求出某个函数 对应的概率密度函数 。这时候的概率密度函数,就依靠于我们选取的采样策略来定义,它实际上是与最终的概率密度函数接近的一个函数,并不是真真的概率密度函数,所以需要通过多次采样,求平均值的方法来抵消这种近似带来的误差。关于这段内容,等到后面讲解对BRDF进行采样的时候,大家就能够理解。我们对BRDF进行采样的时候,往往很难求出BRDF本身的PDF,而是通过选取合适的采样策略,比如对GGX进行采样来逼近。
公式部分
原始的PBR反射方程:
在解决漫反射辐照问题的时候,我们仅仅需要的是入射光线Wi,但是在解决镜面反射辐照的时候,因为双向反射分布函数:
我们需要的输入变量由入射光Wi和出射(观察)方向Wo两者同时决定,我们不能将Wi和Wo的所有组合都尝试并计算一遍来得出结果(因为性能要求太过庞大),所以我们需要一些别的方法。
Epic Games的split sum approximation 通过将方程分成两部分,分别计算结果再组合的方式来解决这个问题,他们将镜面反射方程变成如下形式
对于第一部分,我们使用预过滤环境贴图来解决,并且我们把粗糙度加入进去。由于粗糙程度的增加,环境贴图需要更多的离散采样向量和更多的模糊反射。对于每一个粗糙度等级,我们将其连续的模糊结果储存在预过滤贴图的mipmap等级中(不熟悉mipmap的可以先去了解一下mipmap的作用)。如下例所示:我们将5个不同模糊等级的结果存储在5个mipmap等级的贴图中。

我们通过获得双向反射分布函数(BRDF)中的输入变量——法线和观察方向及其正态分布函数来生成采样向量和散射强度。但是在这之前,我们无法获取观察向量(因为我们还没有真正绘制物体,现在只是在预处理环境贴图),Epic Games为了解决这个问题,让观察方向总是等于Wo,即下列代码:
vec3 N = normalize(WorldPos);
vec3 R = N;
vec3 V = R;
对于方程的第二部分,该部分就是双向反射分布函数(BRDF)的镜面反射积分。如果我们假设每个方向的入射光的颜色是白的(即L(p,x)=1.0),在给出粗糙度和法线n与光向量Wi的夹角的情况下,我们可以预计算双向反射分布函数(BRDF)的返回值。Epic Games 会根据每个法线n与光向量Wi的组合以及粗糙度来存储一个值到2D的查找纹理当中(LUT),这个贴图也叫做BRDF积分贴图。这个2D查找纹理输出一个scale(不知道这里应该怎么翻译,对应于图片的红色分量)和一个偏移值(绿色分量)为菲涅尔方程提供参数,最终会给予我们第二部分的镜面反射积分:
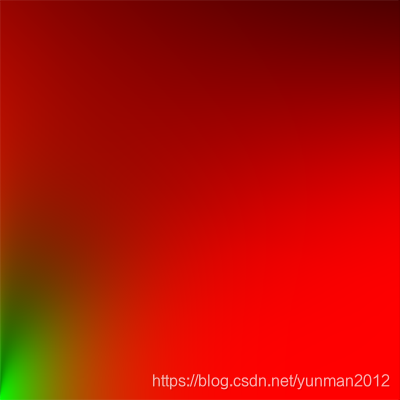
关于前面给到的第二部分方程, 如下:
右边部分要求我们在给出N与W0的夹角、表面粗糙度和菲涅尔F0后对BRDF方程进行卷积。这很像当Li为1.0时对镜面BRDF进行积分。在3个变量的情况下对BRDF进行卷积十分麻烦,但是我们可以把F0移出镜面BRDF方程:
F代表的是菲涅尔方程。将菲涅尔移动到BRDF的分母上,可以得到如下方程:
我们用菲涅尔方程的近似值来代替最右边的菲涅尔方程:
让我们用α来代替(1−ωo⋅h)5(1−ωo⋅h)^5,以便于更方便的解决F0:
然后我们将其分成两部分:
接下来,我们可以把F0提到积分外面,并将α变回原来的式子:
注意!!:因为本身f(p,ωi,ωo)包含菲涅尔方程, 所以我们可以将分母上的F与其抵消~
使用一种相似的方式更早的对环境贴图进行卷积,我们可以通过BRDF方程的输入进行卷积:N与W0的夹角和粗糙度以及存储在纹理中的卷积结果。我们将卷积结果存储在一张2D查找纹理中(LUT),也被称为BRDF积分贴图,我们稍后会在PBR光照着色器中使用它来得到简介镜面反射结果。
BRDF卷积着色器对一个2D平面进行操作,使用2D纹理的坐标作为BRDF 卷积的直接输入(NdotV和粗糙度)。这部分的卷积代码与预过滤卷积代码十分的相似,不同之处是它的采样向量是根据BRDF的几何函数和菲涅尔方程近似值得到的:
vec2 IntegrateBRDF(float NdotV, float roughness)
{
vec3 V;
V.x = sqrt(1.0 - NdotV*NdotV);
V.y = 0.0;
V.z = NdotV;
float A = 0.0;
float B = 0.0;
vec3 N = vec3(0.0, 0.0, 1.0);
const uint SAMPLE_COUNT = 1024u;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
// generates a sample vector that's biased towards the
// preferred alignment direction (importance sampling).
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
vec3 L = normalize(2.0 * dot(V, H) * H - V);
float NdotL = max(L.z, 0.0);
float NdotH = max(H.z, 0.0);
float VdotH = max(dot(V, H), 0.0);
if(NdotL > 0.0)
{
float G = GeometrySmithIBL(N, V, L, roughness);
float G_Vis = (G * VdotH) / (NdotH * NdotV);
float Fc = pow(1.0 - VdotH, 5.0);
A += (1.0 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
A /= float(SAMPLE_COUNT);
B /= float(SAMPLE_COUNT);
return vec2(A, B);
}
void main()
{
vec2 integratedBRDF = IntegrateBRDF(TexCoords.x, TexCoords.y);
FragColor = integratedBRDF;
}
我们生成的这个查找纹理的水平分量代表BRDF的输入n*Wi,竖直分量则是输入的粗糙度。当我们拥有BRDF积分贴图和预过滤环境贴图后,我们可以将两者合并,并得到镜面积分结果:
float lod = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF = texture2D(BRDFIntegrationMap, vec2(roughness, ndotv)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)
只看间接光高光部分输出:
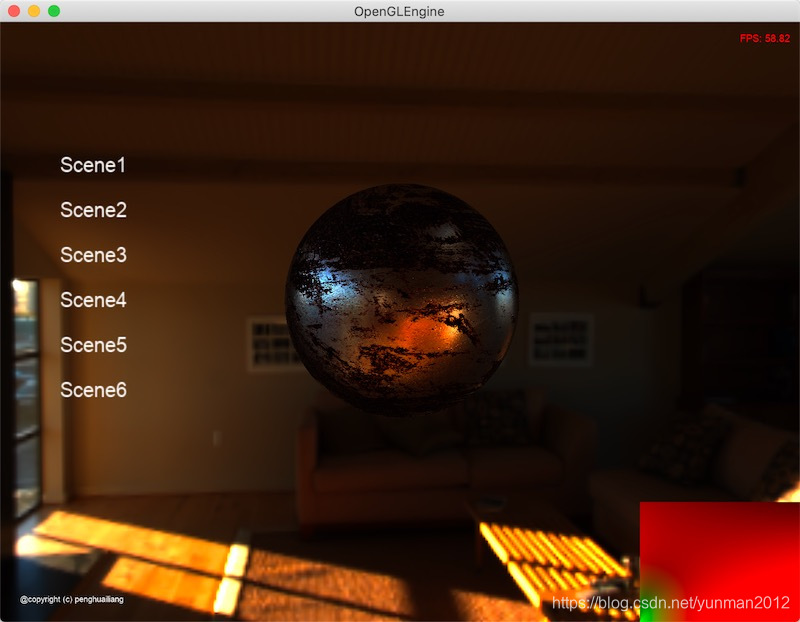
整体PBR渲染输出:
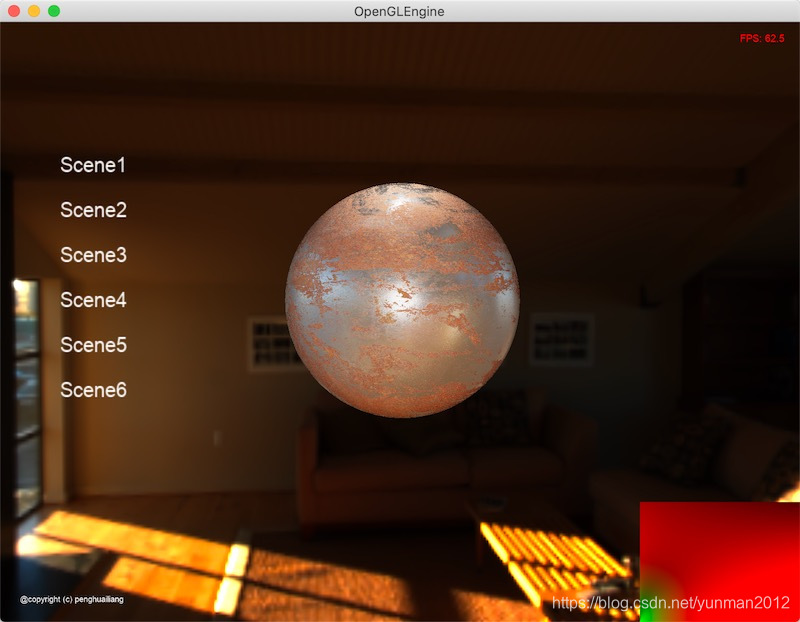
右下角对应的是预过滤环境贴图。
