分治法是一个广泛的概念
// 往往是在merge阶段搞名堂,真正解决问题。
文章目录
1 耗时少又能解决问题的merge
1.1 最大子数组问题
原本需要n^2时间,而发现跨越中点的(确定了中间一点的)最大子数组可以在O(n)时间内解决,
于是分治:T(n) = 2T(n/2) + O(n)
=> O(nlgn)
1.2 最近点对问题(二维欧几里得距离)
原本需要两两遍历一遍O(n^2),而发现跨域中线的点对可以在O(n)时间内解决,
于是分治:T(n) = 2T(n/2) + O(n)
=> O(nlgn)
1.3 找数组中数量过半的那个元素,不存在序关系,只能比较是否相同
该数组平均分为两部分,则主元素为两部分中至少一部分的主元素,故而:
递归地查找两部分P1, P2的主元素m1, m2,若
m1和m2相同,则即为主元素;
m1和m2不同,则主元素必为m1, m2中的一个,O(n)遍历一遍P1, P2就可以找出;
T(n) = 2T(n/2) + O(n)
对于这个问题,选用分治法是因为:
1.在merge阶段,可以巧妙地用O(n)实现,而非直接处理所需的O(n^2);
2.化分出的微小子问题可以轻易的解决。
仍需指出,存在着比分治更快的算法,在O(n)时间内两两遍历每个元素,若两个元素不同,则删去它们,这样不影响剩余部分的主元素。
2 简化重复计算
2.1 大整数乘法
通过观察,简化了需要重复计算的部分
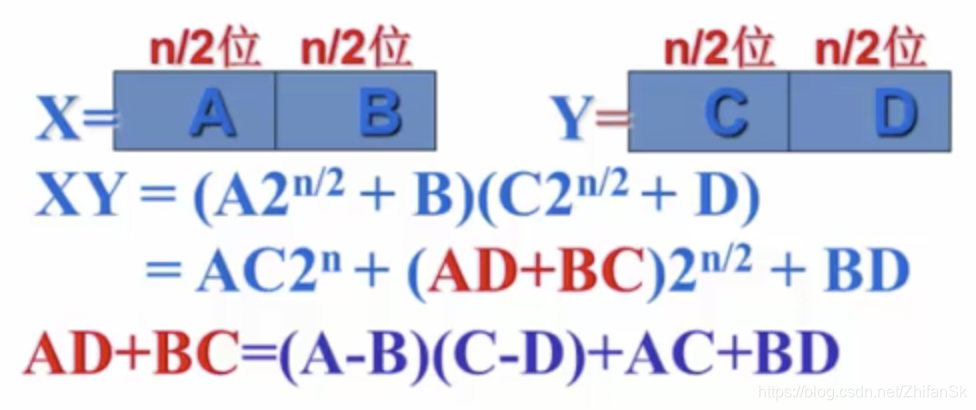
T(n) = 4T(n/2) + O(n)
=> T(n) = 3T(n/2) + O(n)
2.2 矩阵乘法的Strassen乘法
矩阵四等分后乘法直接计算不会比朴素算法快,而在细分发现了重复计算的部分,于是可以省略
2.3 快速幂
在计算幂次乘法的过程中发现了需要重复计算的部分,于是可以简化计算;
本质上,是把较高次幂的运算化分为较低次幂的计算,细分出来的较低次幂容易快速计算,再把它merge起来,分治思想是这样体现的。
