变分自编码器解析

概述

译自https://jaan.io/what-is-variational-autoencoder-vae-tutorial/

在讨论变分自动编码器时，为什么深度学习研究人员和概率机器学习人员会感到困惑？ 什么是变体自动编码器？ 为什么这个词会引起混乱？

这是因为神经网络和概率模型在基本概念和描述语言上存在差异。此教程的目标是弥合这一思想鸿沟，允许在这些领域之间进行更多的协作和讨论，并提供一致的实现方法。

变分自编码器用起来很酷，让我们能够设计复杂的数据生成模型，并将其应用于大型数据集。它可以生成虚构的名人面孔或者高分辨率的数字艺术品图像。这些模型在图像生成和强化学习中获得了非常好的效果。

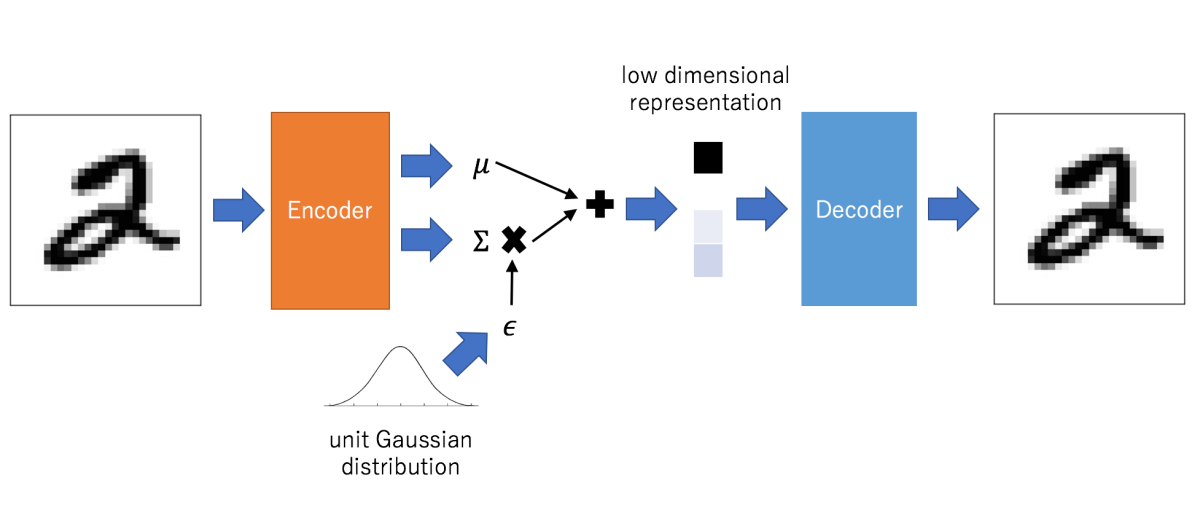
下面本文将从神经网络和概率模型两个角度对其进行讲解。

神经网络角度

以神经网络语言描述的话，VAE包含编码器、解码器和损失函数三部分。编码器将数据压缩到隐空间\((z)\)中。 解码器根据隐状态\(z\)重建数据。

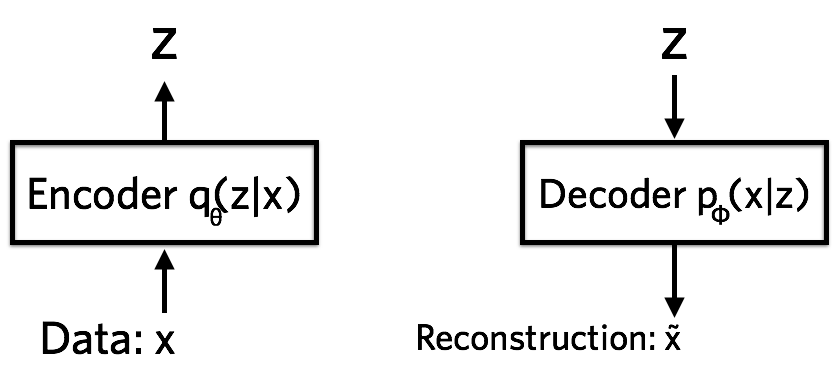
编码器是一个神经网络，它的输入是数据点\(x\)，输出是隐状态\(z\)，它的参数\(\theta\)包括权重和偏置。为了更具体地说明，假设\(x\)是一副\(28\times 28\)的手写数字图片，通常被重塑成784维的向量。编码器需要将728维的数据\(x\)编码到隐空间\(z\)，而且\(z\)的维度要比784小很多。这通常被称为“瓶颈”，因为编码器必须学习将数据有效压缩到此低维空间的方法。假设编码器表示为\(q_{\theta}(z|x)\)，我们注意到较低维的隐空间是随机的：编码器将参数输出到\(q_{\theta}(z|x)\)，这是高斯概率密度，然后我们可以从该分布中采样以获得\(z\)的噪声值。

解码器也是一个神经网络，它的输入是隐状态\(z\)，输出是数据的概率分布，它的参数\(\phi\)也包括权重和偏置，可以把解码器表示为\(p_{\phi}(x|z)\)。还是以上面例子讲解，假设每个像素取值是0或者1，一个像素的概率分布可以用伯努利分布表示。因此解码器输入\(z\)之后，输出784个伯努利参数，每个表示图中的一个像素是取0还是取1。原始784维图像\(x\)的信息是无法获取的，因为解码器只能看到压缩的隐状态\(z\)。这意味着存在信息丢失问题。

变分自编码器的损失函数是带正则项的负对数似然函数。因为所有数据点之间没有共享表示，因此每个数据点的损失\(l_i\)是独立的，总损失\(\mathcal{L}=\sum_{i=1}^N l_i\)是每个数据点损失之和。而数据点\(x_i\)的损失\(l_i\)可以表示为：

\[l_i(\theta,\phi)=-\mathbb{E}_{z \sim p_{\theta}(z|x_i)}[\log_{p_{\phi}}(x_i|z)] + KL(p_{\theta}(z|x_i)||p(z)) \]

第一项是重构损失，或者说是数据点\(x_i\)负对数似然的期望。第二项KL散度是正则项，它衡量了分布\(p\)和\(q\)的近似程度，也就是用\(q\)表示\(p\)时有多少信息丢失了。

在变分自编码器中，\(p(z)\)被指定为标准正态分布，也就是\(p(z)=\text{Normal}(0,1)\)。如果编码器输出的\(z\)不服从标准正态分布，将会在损失函数中对编码器施加惩罚。正则化用来保持每个手写数字的隐状态\(z\)充分多样但又具有意义。如果不使用的话，编码器可能简单地将每个数据点映射到欧几里德空间的不同区域，这会出现问题。比如有两个包含数字2的手写图片\(2_{a}\)和\(2_b\)，它们可能会编码成非常不同的隐状态\(z_a\)和\(z_b\)。而我们希望在隐空间中相同数字的隐状态应该是彼此靠近的，因此需要用正则项进行约束。

概率模型角度

现在，让我们忘掉所有深度学习和神经网络知识，从概率模型的角度重新看变分自编码器。在最后，我们仍然会回到神经网络。

在概率模型框架下，变分自编码器中数据点\(x\)和隐变量\(z\)的联合概率表示为\(p(x,z)=p(x|z)p(z)\)。此时，对于每个数据点\(i\)，生成过程可以表示如下：

• 采样隐变量\(z_i \sim p(z)\)
• 采样数据点\(x_i \sim p(x|z)\)

这可以用概率图模型表示；

这就是我们从概率模型角度讨论变分自编码器时的核心问题。隐状态\(z\)从先验分布\(p(z)\)中采样得到，然后数据点\(x\)从以\(z\)为条件的分布\(p(x|z)\)中产生。整个模型定义了数据和隐状态的联合分布\(p(x,z)=p(x|z)p(z)\)，对于手写数字而言，\(p(x|z)\)就是伯努利分布。

现在，我们可以考虑如何根据给定的观测数据推断出隐变量，或者说计算后验概率\(p(z|x)\)。根据贝叶斯定理：

\[p(z|x)=\frac{p(x|z)p(z)}{p(x)} \]

考虑分母\(p(x)\)，它可以通过\(p(x)=\int p(x|z)p(z)dz\)计算。不幸的是，该积分需要指数时间来计算，因为需要对所有隐变量进行计算。 因此，我们需要近似该后验分布。

变分推断使用分布族\(q_{\lambda}(z|x)\)来近似后验分布，参数\(\lambda\)指示具体分布族。比如，如果\(q\)是高斯分布的话，\(\lambda\)就是每个数据点隐状态的均值和方差\(\lambda_{x_i}=(\mu_{x_i},\sigma_{x_i}^2)\)。

那么怎么知道用分布\(q(z|x)\)近似真实的后分布\(p(z|x)\)到底好不好呢？我们可以用KL散度来衡量：

\[KL\left(q_{\lambda}(z|x)||p(z|x)\right) = \\ \mathbb{E}_q[\log q_{\lambda}(z|x)] - \mathbb{E}_q[\log p(x,z)] + \log p(x) \]

我们的目标是找到使得KL散度最小的变分参数\(\lambda\)。最优的后验分布就可以表示为：

\[q_{\lambda^*}(z|x)=\arg\min_{\lambda}KL\left(q_{\lambda}(z|x)||p(z|x)\right) \]

但是这依然无法进行计算，因为仍然会涉及到\(p(x)\)，我们还需要继续改进。引入下面这个函数：

\[ELBO(\lambda)= \mathbb{E}_q[\log p(x,z)] - \mathbb{E}_q[\log q_{\lambda}(z|x)] \]

我们可以将ELBO与上面的KL散度计算公式结合，可以得到：

\[\log p(x)= ELBO(\lambda) + KL\left(q_{\lambda}(z|x)||p(z|x)\right) \]

由于KL散度始终是大于等于0的，这意味着最小化KL散度等价于最大化ELBO。ELBO(Evidence Lower BOund)让我们能够对后验分布进行近似推断，可以从最小化KL散度中解脱出来，转而最大化ELBO。而后者在计算上是比较方便的。

在变分自编码器模型中，每个数据点的隐状态\(z\)是独立的，因此ELBO可以被分解成所有数据点对应项之和。这使得我们可以用随机梯度下降来更新共享参数\(\lambda\)。每个数据点的ELBO表示如下：

\[ELBO_i(\lambda)=\mathbb{E}q_{\lambda}(z|x_i)[\log p(x_i|z)] - KL(q_{\lambda}(z|x_i)||p(z)) \]

现在可以再用神经网络来进行描述了。我们使用一个推断网络(或编码器)近似后验\(q_{\theta}(z|x,\lambda)\)，该推断网络输入数据\(x\)然而输出参数\(\lambda\)。再使用一个生成网络(或解码器)参数化\(p(x|z)\)，该生成网络输入隐状态和参数，输出数据分布\(p_{\phi}(x|z)\)。\(\theta\)和\(\phi\)是推断网络和生成网络的参数。此时我们可以使用这两个网络来重写ELBO：

\[ELBO_i(\theta,\phi)=\mathbb{E}q_{\theta}(z|x_i)[\log p_{\phi}(x_i|z)] - KL(q_{\theta}(z|x_i)||p(z)) \]

可以看到，\(ELBO_i(\theta,\phi)\)和我们之前从神经网络角度提到的损失函数就差一个符号，即\(ELBO_i(\theta,\phi)=-l_i(\theta,\phi)\)。我们仍然可以将KL散度看作正则项，将期望看作重构损失。但是概率模型清楚解释了这些项的意义，即最小化近似后验分布\(q_{\lambda}(z|x)\)和模型后验分布\(p(z|x)\)之间的KL散度。

模型参数呢？我们忽略了这一点，但这很重要。术语“变分推断”通常是指相对于参数\(\lambda\)最大化ELBO。我们还可以相对于模型参数\(\phi\)最大化ELBO。这项技术称为变分EM（期望最大化），因为我们正在相对于模型参数最大化数据的期望对数似然。

这就是全部了，我们遵循了变分推断的方法，定义了：

• 概率模型\(p\)表示隐变量和数据的分布
• 隐状态的变分分布族\(q\)，用于近似后验分布

然后我们利用变分推断算法学习变分参数（在ELBO上用梯度上升学习\(\lambda\)），利用变分EM算法学习模型参数（在ELBO上用梯度上升学习\(\phi\)）。

实验

现在可以模型进行一些实验了，两种方式衡量实验进度：从先验分布或后验分布采样。为了更好地解释学习到的潜在空间，我们可以可视化隐变量的后验分布\(q_{\lambda}(z|x)\)。

可以参考作者给出的代码：https://github.com/altosaar/variational-autoencoder。

Mean-field推断和amortized推断

这个问题对我来说非常令人困惑，对于来自深度学习背景的人来说，它可能会更加令人困惑。在深度学习中，我们考虑输入和输出，编码器和解码器以及损失函数。在学习概率建模时，这可能导致模糊，不精确的概念。

让我们讨论Mean-field推断和amortized推断的不同之处。这是我们在进行近似推断以估计隐变量的后验分布时所面临的选择。这可能涉及到各种问题：我们是否有大量数据？我们有大量计算资源吗？每个数据点的隐变量是局部独立的，还是全局共享的？

Mean-field变分推断是指在没有共享参数的情况下对\(N\)个数据点进行分布推断：

\[q(z)=\prod_i^N q(z_i;\lambda_i) \]

这意味着每个数据点都有自由参数\(\lambda_i\)（例如对于高斯隐变量，\(\lambda_i =(\mu_i，\sigma_i)\)）。对于新数据点，我们需要针对其mean-field参数\(\lambda_i\)最大化ELBO。

amortized推断是指“摊销”数据点之间的推断成本。一种方法是在数据点之间共享（摊销）变分参数\(\lambda\)。例如，在变分自动编码器中，推断网络的参数\(\theta\)，这些全局参数在所有数据点之间共享。如果我们看到一个新的数据点并想看一下它的近似后验\(q(z_i)\)，我们可以再次运行变分推断（最大化ELBO直到收敛），或者直接使用共享参数。 与Mean-field变分推断相比，这可能是一个优势。

哪一个更灵活呢？Mean-field变分推断严格来说更具表达性，因为它没有共享参数。每个数据点独立的参数\(\lambda_i\)可以确保近似后验最准确。但另一方面，通过在数据点之间共享参数可以限制分布族的容量或表示能力（例如，使用在数据之间共享权重和偏差的神经网络）。

重参数化技巧

实现变分自编码器的最后一件事是如何对随机变量的参数求导数。如果给定从分布\(q_{\theta}(z|x)\)中得出的\(z\)，并且我们想要对\(\theta\)取\(z\)函数的导数呢？此时采样不可导，进而导致模型无法反向传播。

对于某些分布，可以以巧妙的方式重新设置样本的参数，也就是重参数化。例如，在均值\(\mu\)和标准偏差\(\sigma\)的正态分布变量中，我们可以像这样从中采样：

\[z = \mu + \sigma \odot \epsilon \]

其中\(\epsilon \sim Normal(0,1)\)。首先从从均值为0,标准差为1的高斯分布中采样,再放缩平移得到\(z\)。这样从\(\epsilon\)到\(z\)只涉及了线性操作(平移缩放)，采样操作在神经网络计算图之外。

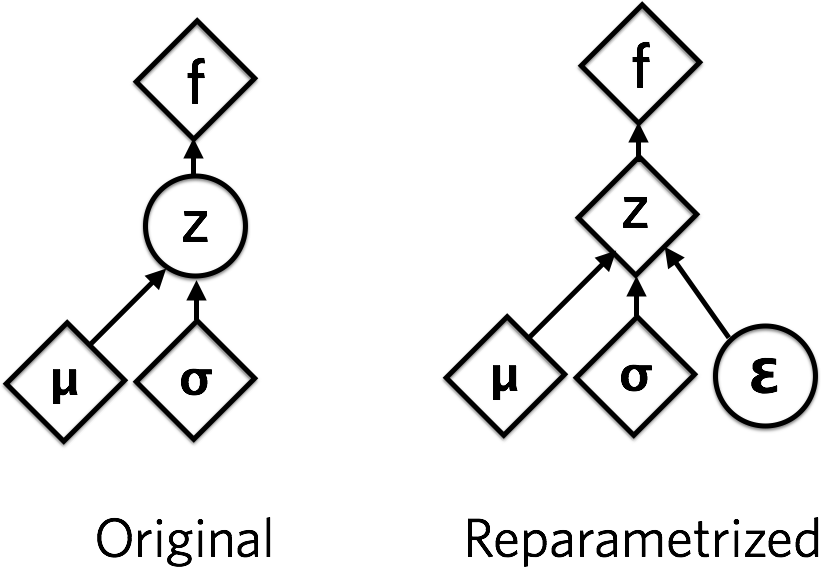
这张图表示了重参数化的形式，其中圆是随机节点，菱形是确定性节点。

由于水平有限，文中难免出现部分错误，还望交流指出！