决策树

自编程实现及可视化详见：https://blog.csdn.net/leemusk/article/details/105040134

0. 基本了解

优点：

计算复杂度不高；
输出结果易于理解，解释性强；
对中间值的缺失不敏感；
可以处理不相关特征数据；

缺点：

可能会产生过度匹配问题，即当子树过大时，可能会造成过拟合，需要进行剪枝。

伪代码实现：

createBranch()
IF so return 类标签;
ELSE
	寻找划分数据集最好的特征（重点部分，根据不同的划分方式产生ID3, C4.5, CART等不同类型的决策树）
	划分数据集
	创建分支节点
		for 每个划分的子集
			调用函数createBranch并增加返回结果到分支节点中
	return 分支节点

1. 基本概念

熵 $H(D)$ ：指混乱程度，比如若实例A的类别都是一样的，则混乱程度则为0，越混乱，熵越大
经验熵 $H(D)$ ：熵是有数据统计得到的情况下，称为经验熵
条件经验熵 $H(D | C_k)$ ：条件熵是由数据统计得到的情况下，称为经验条件熵
信息增益 $g(D, C_k)$ ：即数据集根据某特征分类前后混乱程度的变化大小，变化越大，代表该特征分类的效果越高。
信息增益比 $g_R(D, C_k)$ ：信息增益与数据D关于特征 $C_k$ 的熵的比
基尼指数 $Gini(D)$ ：表示集合的不确定性；
基尼指数 $Gini(D,A)$ ：表示经A = a分割后集合D的不确定性。基尼指数越大，样本的不确定性就越大。

2. 本章概要

决策树：决策树是一种自上而下，对样本数据进行树形分类的过程，有节点和有向边组成。节点分为内部节点和叶节点，每个内部节点表示一个特征或属性，每个叶节点表示类别。
分类决策树模型是基于特征对实例进行分类的树形结构。决策树可以转换为一个If-then规则的集合，也可以看做是定义在特征空间划分上的类的条件概率分布。
决策树学习旨在构建一个与训练数据拟合很好，并且复杂度较小的决策树，因为从可能的决策树中直接选取最优决策树是NP完全问题。现实中采用启发式方法学习次优的决策树。
决策树学习算法包括3部分：特征选择，树的生成和树的剪枝。常用的算法有ID3、C4.5、 CART。
特征选择的目的在于选取对训练数据能够分类的特征。特征选择是其准则。常用的准则如下：
（1）样本集合D对特征A的信息增益(ID3)
$g(D,A) = H(D）- H(D|A) \\ H(D) = - \sum_{k=1}^{K} \frac {|C_k|} {|D|} log_2\frac {|C_k|}{|D|} \\ H(D|A) = \sum_{i=1}^n \frac {D_i} {D} H(D_i)$
其中， $H(D)$ 是数据集D的熵， $H(D_i)$ 是数据集 $D_i$ 的熵， $H(D|A)$ 是数据集D对于特征A的条件熵。 $D_I$ 是D中特征A取第 i 个值的样本自己， $C_k$ 是D中属于k类的样本自己。n是特征A取值的个数，K是类的个数。
（2）样本集合D对特征A的信息增益比（C4.5）
$g_R(D,A) = \frac {g(D,A) } {H_A(D)}$

注意 $H(D)$ 和 $H_A(D)$ 的区别：
$H(D)$ 表示数据集D的类别的混乱程度，即计算类别的熵；
$H_A(D)$ 表示数据集D上，特征A的的混乱程度，计算主题为特征A的值。即数据集D关于特征A的特征的值的熵，

（3）样本集合D的基尼指数（CART）
$Gini(D) = 1 - \sum_{k=1}^K (\frac {|C_k|} {|D|})^2$
特征A条件下集合D的基尼指数：
$Gini(D,A) = \frac {|D_1|} {|D|} Gini(D_1) + \frac {|D_2|} {|D|} Gini(D_2)$
决策树的生成。通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标，从根节点开始，递归地产生决策树。这相当于用信息增益或其他准则不断地选取局部最用的特征，或将训练集分割为能够基本正确分类的子集。
决策树的剪枝。由于生产的决策树存在过拟合问题，需要对它进行剪枝，以简化学到的决策树。决策树的剪枝，往往从已生成的树上减掉一些叶节点或叶节点以上的子树，并将其父节点或根节点或作为新的叶节点，从而简化为生产的决策树。
剪枝主要分为预剪枝和后减枝。预剪枝通过设置阈值完成，当对某节点进行分割时发现该节点的熵小于设定的遇着，则将其作为单节点，不再进行分割。后剪枝是在决策树完成之后，通过子树的损失函数的计算，来决定是否将该节点作为单节点。

3. 生成算法

ID3, C4.5, CART决策树的差异：
(1) 从评价标准看：
ID3 采用信息增益作为评价标准，信息增益反映的是给定条件以后不确定性（混乱程度）减少的程度。

C4.5采用信息增益比作为评价标准，一定程度上对取值比较多的特征进行惩罚，避免ID3出现过拟合的特性，提高了决策树的泛化能力。

CART采用基尼指数 （分类问题）/ 最小平方误差（回归问题）作为评价标准，使用二元切割法，所有CART必须是一颗二叉树。

(2) 从样本类型的角度：

   ID3只能处理离散型变量，C4.5和CART可以处理连续型变量；

(3) 从应用的角度：

   ID3和C4.5只能用于分类任务，而CART可以应用于回归任务；

(4) 从实现细节，优化过程等角度：

   1. ID3对样本缺失特征值比较敏感，而C4.5和CART可以对缺失值进行不同方法的处理；
   2. CART必须是二叉树，ID3和C4.5则不一定；
   3. ID3和C4.5通过剪枝来权衡树的准确性和泛化能力，? 而CART直接利用全部数据发现所有可能的树结构进行对比；

算法总览：

ID3算法：
C4.5算法：
针对ID3的改进：
a. 以信息增益作为划分训练数据集的特征，存在容易偏向于选择取值较多的特征的问题
b. 判断信息增益容易造成过拟合，比如一个特征有很多类别的时候，每一类只有一个样本，导致条件熵为0，信息增益很大，但由此会导致泛化能力很差，即产生过拟合，所以提出信息增益比，改进过拟合。

在这里插入图片描述

CART算法（回归）
回归问题中采用最小平方误差作为评价标注

4 CART算法（分类）

分类问题中采用基尼指数最小作为评价标注

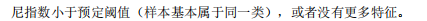
成成算法的停止条件：没有可选择的特征，或样本集的基尼指数 / 信息增益比小于预设的阈值，或所有实例都属于同一类。

4. 剪枝

损失函数：
$C_ \alpha(T) = C(T) + \alpha{|T|} = \sum_{t=1}^{|T|}N_tH_t(T) + \alpha|T| \\ H_t(T) = - \sum_k \frac {N_tk} {N_k} log N_{tk} {N_t}$
|T| 为惩罚项，是叶子节点的个数，代表了模型的复杂度
$\alpha$ 是对模型的复杂度和与训练模型的拟合程度的权衡。

针对ID3, C4.5的后剪枝算法：
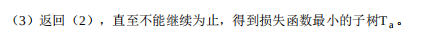
CART的后减枝算法
主要思想：

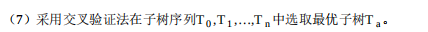
$g(t)$ :剪枝后损失函数减小的程度
$C_\alpha(t)$ ：以t为单结点树的损失函数
$C_\alpha(T_t)$ ：以t为根节点的子树的损失函数
$C(T_t)$ ：以t为根节点的子树的训练误差

训练误差和损失函数的关系：
损失函数 = 训练误差 + 惩罚项

5. 基尼指数、熵之半、分类误差率的关系

在这里插入图片描述

6. 作业

根据表5.1 利用信息增益比生产决策树

（1）计算经验熵 $H(D)$
$H(D) = -\frac 6 {15} log_2 \frac 6 {15}-\frac 9 {15} log_2 \frac 9 {15} = 0.971$
（2）计算每个特征的经验条件熵 $H(D|C_k)$
$H(D|C_1) = \frac 5 {15} (-\frac 3 {5} log_2 \frac 3 {5}-\frac 2 {5} log_2 \frac 2{5}) + \frac 5 {15} (-\frac 3 {5} log_2 \frac 3 {5}-\frac 2 {5} log_2 \frac 2{5}) + \frac 5 {15} (-\frac 4 {5} log_2 \frac 4 {5}-\frac 4 {5} log_2 \frac 4{5}) =0.888 \\ H(D|C_2) = \frac 5 {15} (-\frac 5{5} log_2 \frac 5 {5}) + \frac {10} {15} (-\frac 6 {10} log_2 \frac 6 {10}-\frac 4 {10} log_2 \frac 4{10}) = 0.647 \\ H(D|C_3) = \frac 9 {15} (-\frac 6 {9} log_2 \frac 6 {9}-\frac 3 {9} log_2 \frac 3{9}) + \frac 6 {15} (-\frac 6 {6} log_2 \frac 6 {6}) = 0.551 \\ H(D|C_4) = \frac 5 {15} (-\frac 4 {5} log_2 \frac 4 {5}-\frac 1 {5} log_2 \frac 1{5}) + \frac 6 {15} (-\frac 2 {6} log_2 \frac 2 {6}-\frac 4{6} log_2 \frac 4{6}) + \frac 4 {15} (-\frac 4 {4} log_2 \frac 4 {4}) = 0.608$

（3）计算信息增益 $g(D, C_k)$
$g(D, C_1) = H(D) - H(D | C_1) = 0.083 \\ g(D, C_2) = H(D) - H(D | C_2) = 0.324 \\ g(D, C_3) = H(D) - H(D | C_3) = 0.42 \\ g(D, C_4) = H(D) - H(D | C_4) = 0.363$

（4）计算训练数据集D关于特征 $C_k$ 的值的熵 $H_A(D)$
$H_{C_1}(D) = - \frac 5 {15} log_2 \frac 5 {15} - \frac 5 {15} log_2 \frac 5 {15} - \frac 5 {15} log_2 \frac 5 {15} = 1.584 \\ H_{C_2}(D) = - \frac 5 {15} log_2 \frac 5 {15} - \frac {10} {15} log_2 \frac {10} {15} = 0.918 \\ H_{C_3}(D) = - \frac 9 {15} log_2 \frac 9 {15} - \frac 6 {15} log_2 \frac 6 {15} = 0.97 \\ H_{C_4}(D) = - \frac 5 {15} log_2 \frac 5 {15} - \frac 4 {15} log_2 \frac 4 {15} - \frac 6 {15} log_2 \frac 6 {15} = 1.566$

（5）计算每个特征 $C_k$ 的信息增益比 $G_R(D,C_k)$
$G_R(D,C_1) = \frac {g(D, C_1)} {H_{c_1}(D)} = 0.052 \\ G_R(D,C_2) = \frac {g(D, C_2)} {H_{c_2}(D)} = 0.353 \\ G_R(D,C_3) = \frac {g(D, C_3)} {H_{c_3}(D)} = 0.433 \\ G_R(D,C_4) = \frac {g(D, C_4)} {H_{c_4}(D)} = 0.231$

（6）选取信息增益比最大的特征 $C_3$ ，即“有自己的房子”，作为分支的特征条件，将数据集分为两部分D1, D2，并将该节点下的数据集中的实例最多的类 $C_k$ 作为该节点的类。
（7）分别对D1, D2进行分类。首先对D1进行分析，可以得知D1的类别只有“是”，所有将其作为单节点。在分析D2, D2中两种类别都有，无法作为单节点，计算除 $C_3$ 以外的特征中信息增益比最大的特征。计算过程同（1）- （6）。
（8）递归计算，直至没有可选择的特征，或样本集的基尼指数 / 信息增益比小于预设的阈值，或所有实例都属于同一类。
证明CART剪枝算法中，当 $\alpha$ 确定时，存在唯一的最优子树 $T_\alpha$ ，是损失函数 $C_\alpha(T)$ 最小。

证明：首先需要了解的是：内部节点是否剪枝只与以当前节点为根节点的子树有关。
通过反证法证明：假设有多个子树是最优的；
有两种情况：
第一种：叶节点回缩到其父节点之前与之后的整体树 $T_A$ ， $T_B$ 都是最优子树。
因为根据剪枝的原理，只有 $T_B$ 优于 $T_A$ 的情况下，才会将叶节点回缩到其父节点。矛盾。
第二中：对左子树的叶节点回缩到其父节点之后的子树 $T_A$ ，对右子树的叶节点回缩到其父节点的子树 $T_B$ 。
若两者都是最优子树，则进一步可推断将 $T_A$ 的右子树的叶节点回缩至父节点与将 $T_B$ 的左子树的叶节点回缩至其父节点的子树都为最优子树，而这这两者是同一颗子树，所以矛盾。
假设不成立。所有最优子树唯一。
尝试调用sklearn.tree.DecisionTreeClassifier模块，训练数据集采用课本例题5.1的数据，判断是否应该批准下列人员的贷款申请。

from sklearn.tree import DecisionTreeClassifier
from sklearn import preprocessing
import numpy as np 
import pandas as pd 
import time 

# 可视化需要的库
from sklearn import tree
import pydotplus

def show(clf, features, y_types):
    # 决策树的可视化
    dot_data = tree.export_graphviz(clf, out_file=None,
                                    feature_names=features,
                                    class_names=y_types,
                                    filled=True, rounded=True,
                                    special_characters=True)
    graph = pydotplus.graph_from_dot_data(dot_data)
    #Image(graph, create_png())
    graph.write_png(r'DT_show.png')

def main():
    start = time.time()

    features = ['age','work','house','credit']
    x_train = pd.DataFrame([['青年','否','否', '一般'],
                        ['青年','否','否', '好'],
                        ['青年','是','否', '好'],
                        ['青年','是','是', '一般'],
                        ['青年','否','否', '一般'],
                        ['中年','否','否', '一般'],
                        ['中年','否','否', '好'],
                        ['中年','是','是', '好'],
                        ['中年','否','是', '非常好'],
                        ['中年','否','是', '非常好'],
                        ['老年','否','是', '非常好'],
                        ['老年','否','是', '好'],
                        ['老年','是','否', '好'],
                        ['老年','是','否', '非常好'],
                        ['老年','否','否', '一般']])
    y_train = pd.DataFrame(['否', '否', '是', '是', '否', '否', '否', '是', '是', '是', '是', '是', '是', '是', '否'])

    # 数据预处理
    le_x = preprocessing.LabelEncoder()
    le_x.fit(np.unique(x_train))
    x_train = x_train.apply(le_x.transform)
    print(x_train)

    le_y = preprocessing.LabelEncoder()
    le_y.fit(np.unique(y_train))
    y_train = y_train.apply(le_y.transform)

    # 调用DecisionTreeClassifier
    clf = DecisionTreeClassifier()
    clf.fit(x_train, y_train)

    # 可视化
    show(clf, features, [str(k) for k in np.unique(y_train)])

    # 用训练得到的模型进行预测
    x_new = pd.DataFrame([['青年','否','是','一般']])
    x = x_new.apply(le_x.transform)
    y_predict = clf.predict(x)

    # 结果输出
    x_show = [{features[i]:x_new.values[0][i]} for i in range(len(features))]
    print("{0} 被分类为： {1}".format(x_show, le_y.inverse_transform(y_predict)))
    print("time:{:.4f}s".format(time.time()-start))

if __name__=="__main__":
    main()

leemusk

发布了21 篇原创文章 · 获赞 0 · 访问量 392

私信关注

统计学习方法笔记---决策树

决策树