计量--一元线性回归模型
一、回归分析概述
1.变量之间的关系
确定性现象(函数关系),例长方形的周长
非确定性现象(统计相关关系),例身高和体重
2.相关关系与回归分析
相关分析:研究两(或多个)变量的相关性及相关程度(使用相关系数表示)
回归分析:已经存在相关关系,求解其因果关系,变量地位不对等(一因一国),根据自变量的变化可以预测运动规律。
举个栗子:
(1)打篮球的人个子更高。
不对,现实是个子更高的人选择了打篮球,属于因果倒置。
(2)社会地位高的人寿命更长。
不对,社会地位高受到的医疗较好,医疗较好导致寿命长一些。
Tips:因果关系的前提:时间先后。
3、相关分析分为线性和非线性(提示:若不相关则将相关性赋为0)
线性相关:
两个变量:计算协方差、相关系数
多个变量:计算偏相关系数、复相关系数
二、总体回归函数(PRF)
在给定解释变量X的条件下,被解释变量Y的期望轨迹称为总体回归曲线,其对应的函数
E(Y|X)=f(X)
F最简形式为线性函数。其截距、斜率为线性回归系数,表达式如下所示,其中β0代表自发消费,β1代表边际消费趋向。
E(Y|X)=β0+β1X
识别:因变量Y为被解释变量、被预测变量、回归子、响应变量,自变量X为解释变量、预测变量、回归元、控制变量。
三、随机误差项
将一个真实Y减去它的均值,则为离差:
μ=Y-E(Y|X)
则
Y=E(Y|X)+μ
说明被解释变量由两部分组成,一部分给定X后便确定,另一部分由于随机因素的参与,而反应自身的波动情况。
随机误差项的含义:
1、未知的影响因素
2、残缺数据
3、众多细小因素
4、数据观测误差
5、模型设定误差
6、内在随机性
四、样本回归函数
首先要认清一个基本事实:总体永远是未知的。总体参数的取值、方差等都是不可获知的,计量学的目的便是:由样本推断总体。
从样本散点中拟合出一条直线,用来近似地替代总体回归线。
例如,一元线性回归:
![]()
注意估计值的符号(记得戴帽子)
重点区分:
**总体回归函数PRF:
E(Y)=β0+β1Xi (i=1,2,,,,n)
PRF随机形式:
E(Y)=β0+β1Xi +μi
**样本回归函数SRF:
![]()
SRF随机形式:
![]()
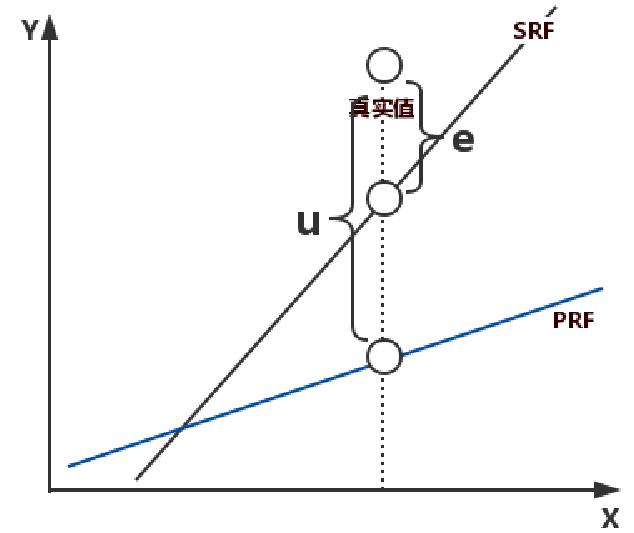
一个是根据总体数据进行回归,一个根据样本数据进行后归,回归结果加上各自的随机误差后,都可以得到真实值。
五、模型假设
假设一:模型无设定偏误问题(正确的变量、正确的函数形式)。
假设二:X是确定性变量(非随机变量)。
假设三:X至少取两个以上不同的值,且样本方差收敛(若X是定值,则问题的意义就会发生改变)(随着样本容量的增加,方差收敛,这是为了避免时间序列的伪回归的问题)
假设四:误差项”零均值、同方差、零协方差“。(对总体而言,我们希望总体误差的均值为0)(总体方差的相同,保证各点上变异程度相同)(对两个不同的样本点,协方差为0,相关系数为0,派出了两个样本点信息相关的可能)
假设五:随机误差项与解释变量不相关(由前面可以推出)
假设六:随机误差项服从正态分布(均值为0,方差为σ2)(可选项,没有这个假设,它仍自动然成立)
六、参数估计
1.参数估计的普通最小二乘法(OLS)(常使用)
原理:总体误差达到最小 → 最小二乘思想,即残差平方和最小,将这个问题变成最优化问。

结果

或
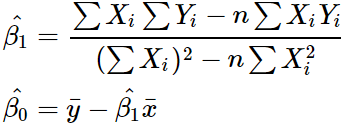
区分: 估计量:随机变量的函数
估计值:具体数值
2.最大似然法(ML)(当OLS不适合时使用ML)
似然:指概率或一种可能性
原理:存在就是合理的(当你观察到一组样本,一定是背后的机制决定了它可以出现在你面前)。出现的概率最大----最大似然法;最小二乘法是总体的误差最小。
![]()
3.参数估计的矩法(MM)
此方法使用较少,暂不讲解。
【薇√Q√同√号√9√7√8√8√9√1√8√1】
一、回归分析概述
1.变量之间的关系
确定性现象(函数关系),例长方形的周长
非确定性现象(统计相关关系),例身高和体重
2.相关关系与回归分析
相关分析:研究两(或多个)变量的相关性及相关程度(使用相关系数表示)
回归分析:已经存在相关关系,求解其因果关系,变量地位不对等(一因一国),根据自变量的变化可以预测运动规律。
举个栗子:
(1)打篮球的人个子更高。
不对,现实是个子更高的人选择了打篮球,属于因果倒置。
(2)社会地位高的人寿命更长。
不对,社会地位高受到的医疗较好,医疗较好导致寿命长一些。
Tips:因果关系的前提:时间先后。
3、相关分析分为线性和非线性(提示:若不相关则将相关性赋为0)
线性相关:
两个变量:计算协方差、相关系数
多个变量:计算偏相关系数、复相关系数
二、总体回归函数(PRF)
在给定解释变量X的条件下,被解释变量Y的期望轨迹称为总体回归曲线,其对应的函数
E(Y|X)=f(X)
F最简形式为线性函数。其截距、斜率为线性回归系数,表达式如下所示,其中β0代表自发消费,β1代表边际消费趋向。
E(Y|X)=β0+β1X
识别:因变量Y为被解释变量、被预测变量、回归子、响应变量,自变量X为解释变量、预测变量、回归元、控制变量。
三、随机误差项
将一个真实Y减去它的均值,则为离差:
μ=Y-E(Y|X)
则
Y=E(Y|X)+μ
说明被解释变量由两部分组成,一部分给定X后便确定,另一部分由于随机因素的参与,而反应自身的波动情况。
随机误差项的含义:
1、未知的影响因素
2、残缺数据
3、众多细小因素
4、数据观测误差
5、模型设定误差
6、内在随机性
四、样本回归函数
首先要认清一个基本事实:总体永远是未知的。总体参数的取值、方差等都是不可获知的,计量学的目的便是:由样本推断总体。
从样本散点中拟合出一条直线,用来近似地替代总体回归线。
例如,一元线性回归:
![]()
注意估计值的符号(记得戴帽子)
重点区分:
**总体回归函数PRF:
E(Y)=β0+β1Xi (i=1,2,,,,n)
PRF随机形式:
E(Y)=β0+β1Xi +μi
**样本回归函数SRF:
![]()
SRF随机形式:
![]()

一个是根据总体数据进行回归,一个根据样本数据进行后归,回归结果加上各自的随机误差后,都可以得到真实值。
五、模型假设
假设一:模型无设定偏误问题(正确的变量、正确的函数形式)。
假设二:X是确定性变量(非随机变量)。
假设三:X至少取两个以上不同的值,且样本方差收敛(若X是定值,则问题的意义就会发生改变)(随着样本容量的增加,方差收敛,这是为了避免时间序列的伪回归的问题)
假设四:误差项”零均值、同方差、零协方差“。(对总体而言,我们希望总体误差的均值为0)(总体方差的相同,保证各点上变异程度相同)(对两个不同的样本点,协方差为0,相关系数为0,派出了两个样本点信息相关的可能)
假设五:随机误差项与解释变量不相关(由前面可以推出)
假设六:随机误差项服从正态分布(均值为0,方差为σ2)(可选项,没有这个假设,它仍自动然成立)
六、参数估计
1.参数估计的普通最小二乘法(OLS)(常使用)
原理:总体误差达到最小 → 最小二乘思想,即残差平方和最小,将这个问题变成最优化问。

结果

或
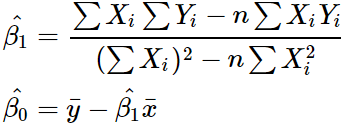
区分: 估计量:随机变量的函数
估计值:具体数值
2.最大似然法(ML)(当OLS不适合时使用ML)
似然:指概率或一种可能性
原理:存在就是合理的(当你观察到一组样本,一定是背后的机制决定了它可以出现在你面前)。出现的概率最大----最大似然法;最小二乘法是总体的误差最小。
![]()
3.参数估计的矩法(MM)
此方法使用较少,暂不讲解。
【薇√Q√同√号√9√7√8√8√9√1√8√1】