相关文章：
二元关系 https://blog.csdn.net/nameofcsdn/article/details/104826886
目录
一，数学归纳法
虽然数学归纳法名字中有“归纳”，但是数学归纳法并非不严谨的归纳推理法，它属于完全严谨的演绎推理法。
数学归纳法是建立在自然数的基础之上的。
1，皮亚诺公理
用日常语言来说，这5条公理可以表述成：
- 0是自然数。
- 每个自然数后面都紧跟着另一个自然数。
- 如果自然数的某子集包含0，且其中的每个元素均有后继元素，那么该子集所包含的数字就是全体自然数。
- 如果两个自然数的后继数相同，那么这两个自然数本身也相同。
- 0不是任何一个自然数的后继数。
其中最为重要的是第三条公理，也叫做归纳公理。
2，第一数学归纳法
使用第一数学归纳法证明一个命题分下面两步：
（1）证明当n= 0时命题成立
（2）假设n=k时命题成立，那么可以推导出在n=k+1时命题也成立。（k代表任意自然数，下同）
这样就可以得到，对于任意自然数n，命题成立。
3，第二数学归纳法（完整归纳法）
证明分两步：
（1）证明当n= 0时，式子成立
（2）假设当n≤k时成立，证明当n=k+ 1时式子也成立
4，跳跃归纳法
证明分两步：
(1) P(0)，P(1)，P(2),…,P(l-1)成立
(2) 假设P(k)成立，可以推出P (k+l)成立，则P(n)对一切自然数n都成立
其中l是常数，代表跳跃步长。
5，螺旋式归纳法
对两个与自然数有关的命题P(n），Q(n），
（1）验证n=0时，P(n）成立
（2）假设P(k）成立，能推出Q(k）成立，假设 Q(k）成立，能推出 P(k+1）成立；
综合（1）（2），对一切自然数n，P(n），Q(n）都成立。
二，数学归纳法的适应领域
所有的数学归纳法，都是通过有限的递降，把问题归结为极小元处的结论。
1，二维命题退化成一维命题
假设有这样一个函数：
int f(int n, int m){
if(n==0)return m;
return f(n-1,m*m);
}用数学归纳法可以证明，f(n,m)=m^(2^n)对于任意自然数n,m成立。
证明：
（1）当n=0时，对于任意m，f(n,m)=m成立
（2）若当n=k时，对于任意m，结论成立，即f(k,m)=m^(2^k)
则对任意u，f(k+1,u)=f(k,u*u）= (u*u)^(2^k) = u^(2^(k+1))，
即结论对k+1也成立。
根据第一数学归纳法，结论对任意n,m成立。
在这个问题中，我们通过n的递降，把问题归结为关于f(0,m)的结论。
2，二维命题
假设有这样一个函数：
int f(int n, int m){
if(n==0)return 1;
if(m==0)return 1;
return f(n-1,m)+f(n,m-1);
}用数学归纳法可以证明，f(n,m)=C(n+m, n)，其中C表示组合数，例如C（5,2）=10
证明：
（1）当n=0时，对于任意m，f(0,m)=C(m,0) 成立
（2）若当n=k时，对于任意m，结论成立，即f(k,m)=C(k+m, k)
则对任意u, f(k+1,u)=f(k,u)+f(k+1,u-1)=f(k+1,u-1)+C(k+u, k)
用第一数学归纳法可以证明，f(k+1,u)=C(k+u+1,k+1)，即结论成立
根据第一数学归纳法，结论对任意n,m成立。
这里我们两次使用第一数学归纳法，而且是嵌套的方式。
3，数学归纳法不能用于实数域
如果f(0)=0，对于任意正整数n, f(n) <= max { f(k) | 0<=k<n }，即f(n)不超过[0,n)上的最大值，那么根据数学归纳法，对于任意自然数n，f(n) <=0
直接把问题域改成实数域的话：
如果f(x)=0在区间[0,1)成立，对于任意实数x>=1，f(x)不超过[0,x)上的最大值，能否得出f(x)<=0恒成立？
答案是不能，而且可以找到一个经典反例：f(x) = （1-D(x)） * G(x)，
其中D表示狄利克雷函数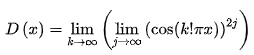
，即当x是有理数时函数值为1，x是无理数时函数值为0
G表示高斯函数，即不超过x的最大整数。
4， 数学归纳法的适应领域
简单来讲，数学归纳法可以适用于自然数组成的n维空间，但是不能用于实数域。
三，正则公理
正则公理是集合论的ZF公理系统中的一条公理。它的表述为：“对任意非空集合x，至少有一 y∈x 使得，要么y不是集合，要么x∩y为空集。”
四，良基关系
设R为集合(或类)U上的一个二元关系，若U的每个非空子集均有R极小元，则称R为U上的一个良基关系。
良序关系一定为良基关系，反之则不成立。
由正则公理知，∈关系为集合论全域V上的良基关系，但不是良序关系。
从直观上讲，被良基化的集合或类，可以通过其上的良基关系对其元素进行分层。
一个二元关系称为是良基的，当且仅当它不包含无穷降链。
五，广义归纳法
在任何一个良集集合上，都有广义归纳法：
(X, R) 是良基关系，并且 P(x) 是 X 上的一个命题，如果满足
（1）对于任意极小元x， P(x)成立
（2）如果 x 不是极小元，对所有满足 y R x 的 y 都有 P(y) 为真，那么 P(x) 也一定为真
那么根据广义归纳法就可以得到，命题P在集合X上恒成立。
六，动态规划
所有的动态规划，一定是在一个良基集合上完成的广义归纳。
我在其他博文中提到的解空间，其实就是这个良基集合。
七，数学归纳法和动态规划的区别
首先，数学归纳法是建立在自然数的基础之上，复杂一点也就二维平面（第一象限），
而动态规划是广义归纳法，常见的良基集合有自然数、自然数区间、二维（或高维）空间的第一象限、树这些。
其次，数学归纳法一般是用来证明一个明确的结论，而且往往已经有解析式，
而动态规划的适用场景多且复杂，需要进行建模抽象（找出递推式）然后才能用归纳法，而且基本不存在解析式。
最后，数学归纳法没有直观的重叠子问题性质，但是动态规划必须要有显式的重叠子问题性质。